Hello everyone. We continue this series of articles on what data science can provide for predicting COVID-19. The first article is here . Today we will talk about the second class of models for predicting the dynamics of the spread of COVID-19. They are based on assumptions about an increase in the incidence and describe the situation in the medium and long term. We are talking with Nikolay Kobalo, CFT Senior Data Engineer.
Let us recall what our conditions are:
Given: Colossal data science capabilities, three talented specialists.
Find: Ways to predict the spread of COVID-19 a week ahead.
Let's move on to the second solution.
- Kolya, hello. Tell us which model you used to solve this problem.
- I took one of the models, which, in my opinion, best suits the occasion. The model is presented in the form of a differential equation and consists of four functions:
1. The number of people who are susceptible to infection with this infection;
2. The number of carriers, that is, people who have already become infected, but do not yet know about it;
3. The number of sick people who infect others;
4. The number of recovered.
As you can see, this model does not take into account mortality from covid. You can see the details of the model on my github: https://github.com/rerf2010rerf/COVID-19-forecast/blob/master/public.ipynb
The model is called SEIR and belongs to a family of compartmental models describing the spread of an epidemic. Models of this family allow describing different types of infections. For example, those for which immunity is developed (or, on the contrary, is not developed). Or those that have (or do not have) an incubation period. In the case of COVID-19, I used a model with an incubation period and the immunity that was produced in people who had been ill.
All polygamous models are systems of first order differential equations. For SEIR they look like this:

Here:
S (t) - (Susceptible) - the number of people susceptible to infection.
E (t) - (Exposed) - the number of carriers, i.e. infected people in whom the disease has not yet manifested due to the incubation period.
I (t) - (Infectious) - infected.
R (t) - (Recovered) - recovered.
N = S + E + I + R - population size. It remains constant, i.e. no one is supposed to die from the disease.
μ is the natural mortality rate.
α is the reciprocal of the incubation period of the disease.
γ is the reciprocal of the average recovery time.
β is the coefficient of intensity of contacts leading to infection.
The life cycle of an individual in the SEIR model looks like this:

A healthy, but not yet ill person (Susceptible) can become infected from an infected (Infectious) person. The probability that a healthy person will become infected is described by the β parameter.
An infected person goes into a state of an infection carrier (Exposed). Carriers are people in whom the disease has not yet manifested itself, that is, they have an incubation period. Carriers cannot infect anyone. The transition of people susceptible to disease into the state of carriers is described by the first two equations of the model (using the term β (I / N)).
After 1 / α days (incubation period) after infection, the carrier enters the infected state (Infectious).
After 1 / γ days (recovery time), the infected person enters the Recovered state. The recovered person develops immunity, and he can no longer contract this infection.
The model also provides for the natural mortality of the population in the population. Mortality in the SEIR model is balanced by fertility, so the total population does not change. At the same time, the number of recovered people in the population will decrease, since newborns will not have immunity. Accordingly, the number of people who have recovered in the population decreases over time. The mortality rate is described by the parameter μ.
- You have coefficients in the model. That is, did you make any assumptions?
- One of my assumptions was that natural mortality in the population can be neglected, i.e. μ = 0. This assumption seems valid, since we want to predict the spread of infection over a short period of time, only a few months.
In addition, the chosen model assumes that those who have recovered become immune to infection, that is, they cannot become infected again.
- And this is so, by the way?
- It seems like, yes. Several re-infections have already been recorded, but more often than not this does not happen. Therefore, we can say that this is so.
- And what is your “contact intensity factor”?
- Here I mean the intensity with which people come into contact with each other and become infected. Roughly speaking, this is the probability that when two people meet, where one is infected and the other is not, the other will eventually get sick.
- Well, how much is it? Close to one?
- No, I selected this parameter according to the data. It depends on the level of self-isolation. For example, if a large part of the population does not come into contact with other people, then the coefficient becomes lower, and if the population actively communicates with each other, then it grows.
- Okay. Do you have a recovery time too? Both alpha and gamma?
- I took alpha equal to 1 / 5.1, this was a known parameter for COVID-19 (the inverse parameter to the incubation period in days). And I selected the range according to the data. This is "convalescence time". "Intensity of contacts", by the way, is also based on data.
- Oh well. Then again, can you tell us what assumptions are made by the models? What does each equation mean?
- The first equation describes the change in the number of susceptible to infection. In particular, the third term says that the more intense the contacts between the infected and the susceptible, the faster the number of susceptible decreases. Moreover, if someone was infected, and then became infected, then he is no longer included in this number. At the beginning of the epidemic, it is equal to the number of people in the population.
Then the number of carriers is taken from those susceptible to infection, that is, a person communicates with an infected person, becomes infected and becomes a carrier of infection. This is described in the second equation. It says that the growth rate of carriers is the greater, the more intense the contacts between the susceptible and the infected, and, on the contrary, the less, the fewer carriers are left at the moment.
The third equation says that the growth rate of the infected is the greater, the more carriers there are now (which turn into infected), and the less, the more infected there are already.
The fourth equation describes the growth rate of those who have recovered, which is the greater, the more infected (who can recover), and the less, the more recovered there are already.
- Sounds like a description of the development of the situation.
- In fact, there are different models. This is the SEIR model, and there is SIR, in which there are no susceptible to infection. There are models with more parameters. There is a model that provides for mortality from infection, but I did not use it.
- Where did you find this model?
- Googled. There is an article on Wikipedia. Found additional articles.
- You also presented the graphics.
- This graph is an example. It is not based on real data. It just shows how the model behaves. She predicts that everyone will eventually get sick and get well.

- Okay, so you took it all, and then what?
- I took the data that is available by country. He assumed that the mortality rate is zero. Rewrote the difours in the form of finite differences:

As a finite difference operator in this solution, a two-sided difference is used.
The number of recovered people R by day is in the initial data, and the number of infected I is equal to the number of confirmed cases minus the number of recovered. So from the last equation you can find γ by optimizing the MALE objective function (ΔR-γI).
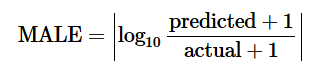
In order to track how quarantine measures affect the development of the epidemic, I complicated my task a little and replaced the β coefficient with the β (t) function - after all, as quarantine is introduced in the country, the infection rate should decrease, which means that in our case β will not be constant. Since we already have all the initial conditions for solving the difura, we can use the optimization to find the function β (t).
- This is a day of difference?
- Day minus the previous day. I plugged in the data and calculated the unknown coefficients.
- Beta and gamma?
- I took Alpha 5.1 days. Accordingly, it was necessary to find beta and gamma - the intensity of contacts and the time of recovery.
- And what happened to you?
- There are graphs. Each region and each country turned out to be different. I decided for each country separately. On the left is a graph of data (black - it was real, red - infected and recovered, predicted by the model). Infected + recovered - it turns out E + R. On the right is the beta coefficient graph. Beta, by the way, is supposed to be time-dependent. Here, the largest jump in β coincides with the time of the quarantine on March 30.
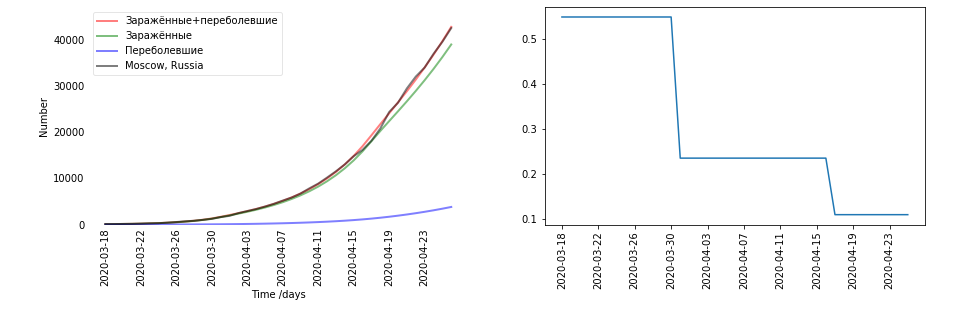
- And you counted it according to the data or assumed so?
- This is already calculated according to the data. This is exactly the result of training in Moscow.
- Did you set the time thresholds yourself?
- I thought that the function has such a two-stage form. And optimized. I just fit the data and find the optimal functions that fit best. I've also tried using functions with a different number of rungs, but the two-stage ones showed better results.
- Let's take a look at the countries, for example, Italy. Well, here you have a different picture ...

- In Italy, quarantine, apparently, worked better. And there are more people who have been ill. The model confirmed that quarantine was introduced on March 9th.
- What did you choose for the final forecast?
- For the final forecast, I chose a constant intensity of contacts and built a model using the last two points. That is, we know the entire previous history, but we take only the last points.
- This is for the prediction for the week?
- Yes. And what happened before was to see how the model behaves. And then I already looked at which function is better to take and at how many points to learn.
- Probably, if you wanted to predict until now, you would have received a different decision. Do you have something that will show how the situation can develop further?
- Yes. But it's not very interesting there. She predicted that everyone in Moscow would be ill by September.
- At one of the meetups you said that according to your forecast, the peak should have been in July. In fact, everything happened a little earlier. What do you think the model did not take into account?
- Probably beta. Perhaps the quarantine has intensified. It is possible that the intensity of contacts has decreased due to the fact that people have been ill, and do not infect, and do not get infected. Beta should somehow depend on it. And here it is not taken into account.
- Well, that is, you say that we can regulate everything with one beta?
- According to known data - yes, we can, with beta and gamma adjust.
- Does your model predict the next wave?
- No, everything is stable: it grows, it grows, it grows and everyone will get sick. Although there is also a seasonality factor. Autumn periods, for example (when the flu, etc., the immune system is weakened). But the model does not take into account all this.
- What are the pros and cons of your model?
- At the time of model compilation, there was little known data. Now both the recovery period and the incubation period are already known (then 5.1 was, now it is more accurately measured). From the pros: it shows the process itself, how it goes. And if we investigate more deeply on the example of other countries, for example, Italy, Germany, how these betas influenced, then it would be possible for us to refine this model and build a more accurate long-term forecast.
, data science – .
, , . - – , , , , .
, , . .He made the coolest model;)