
In a paper recently published in Physical Review Research, we demonstrate how deep learning simplifies the solution of fundamental quantum mechanical equations for real systems. At the same time, not only a fundamental scientific issue is solved, but also prospects for the practical use of the results obtained in the future are opening up.
Researchers will be able to prototype new materials and compounds in silico before trying to synthesize them in the laboratory. Also posted the codefrom this study; thus, computational physics and chemistry teams can build on their work and apply it to a variety of problems. As part of the study, a new neural network architecture, Fermionic Neural Network or FermiNet, was developed, which is well suited for simulating the quantum state of large collections of electrons - and all chemical bonds are based on electrons. FermiNet demonstrated for the first time how to use deep learning to calculate the energy of atoms and molecules from scratch. The resulting model turned out to be accurate enough for practical application and at the time of the publication of the original article (October 2020) it remained the most accurate neural network method used in the industry. It is assumedthat the associated methods and tools can be useful in solving fundamental problems in the natural sciences. The authors of FermiNet are already using it in their work on the convolution of proteins , the dynamics of glassy compounds , quantum chromodynamics on a lattice, and in many other projects helping to translate these developments into practice.
A brief history of quantum mechanics
By mentioning "quantum mechanics", you are likely to puzzle the interlocutor with this topic like no other. Immediately I remember such images as Schrödinger's cat, which paradoxically can be simultaneously alive and dead, as well as elementary particles, which are both corpuscles and waves. In a quantum system, a particle such as an electron does not have a specific location, unlike the situation in classical physics. In quantum physics, the position of an electron is described by a cloud of probabilities - that is, it is smeared over all those points, at each of which an electron may appear. Because of this absurd state of affairs, Richard Feynman found it possible to state: "I think I can safely say that no one understands quantum mechanics."
Despite all this eerie weirdness, the essence of the theory can be expressed in just a few neat equations. The most famous of these, the Schrödinger equation, describes the behavior of particles on a quantum scale in the same way that Newton's equations describe the behavior of bodies on the more familiar macroscopic scales. While the interpretation of this equation will force anyone to grab their heads, its mathematical component is much easier for practical use, due to which the famous professor's "shut up and count" was born, with which they fought off awkward philosophical questions from students.
These equations are sufficient to describe the behavior of all matter familiar to us at the level of atoms and nuclei. An illogical component of quantum mechanics underlies all sorts of exotic phenomena: superconductivity, superfluidity, laser and semiconductors are possible only due to quantum effects. But even such a modest thing as a covalent bond - the basic component of all chemistry - is the result of quantum interactions of electrons. When these rules were finally worked out in the 1920s, scientists realized that for the first time a theory had been created that detailed the work of all chemistry. In principle, quantum equations could simply be adapted for different molecules, solved by taking into account the energy of the system, and then determining which molecules will be stable and which reactions will occur spontaneously. But,when an attempt was made to sit down and calculate the solutions for these equations, it turned out that this is feasible for the simplest atom (hydrogen) and practically not for any other. All other calculations turned out to be too complicated.
The dizzying optimism of those days was beautifully summed up by Paul Dirac:
So, the basic physical laws required for a mathematical theory that would describe most of physics and all of chemistry are already known. The catch is that in practice the application of these laws gives too complex equations, which we are objectively unable to solve. Therefore, it seems desirable to develop approximate methods for the practical application of quantum mechanics.
1929
Many took up Dirac's call, and soon physicists began to develop mathematical methods that would make it possible to approximate the behavior of molecular bonds and other chemical phenomena at a qualitative level. It all started with a rough description of the behavior of electrons - this information is studied in an introductory chemistry course. With this description, each electron is brought into its own orbital, which allows you to calculate the probability that an electron will be found at a specific point in the vicinity of an atomic nucleus. In this case, the shape of each orbital depends on the average shape of all other orbitals. Since in such a description according to the "self-consistent field" model, it is assumed that each electron is attached to only one orbital, this picture very incompletely conveys the real properties of electrons. Still, it's enoughto determine the total energy of the molecule with an error of only about 0.5%.
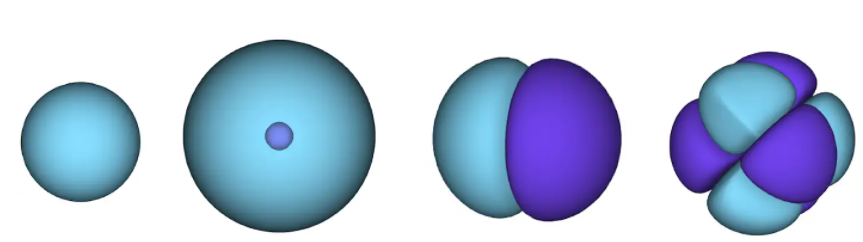
Figure 1 - atomic orbitals. a surface is an area in which an electron is likely to be located. in the blue region the wave function is positive, and in the violet it is negative.
Unfortunately for the practicing chemist, a 0.5% error is too big to be tolerated. The energy of molecular bonds is only a small fraction of the total energy of a system, and the correct prediction of whether a molecule will be stable can often depend on as little as 0.001% of the total energy of the system, or about 0.2% of the remaining "correlation" energy.
For example, while the total energy of electrons in a butadiene molecule is is almost 100,000 kilocalories per mole, the energy difference between the various possible configurations of the molecule is only 1 kilocalorie per mole. That is, if it is necessary to correctly predict the natural shape of the butadiene molecule, the same level of accuracy is required as when measuring the width of a football field with an accuracy of a millimeter.
With the proliferation of electronic computing soon after World War II, scientists developed a whole slew of computational methods that could not be described as self-consistent fields. These methods are denoted by an unimaginable bunch of abbreviations covering the entire alphabet, but each of these methods contains some kind of trade-off between accuracy and efficiency. At one extreme are methods that are inherently accurate, but scale worse than exponentially as the number of electrons increases - so they are not suitable for working with most but the smallest molecules. At the other extreme, there are methods that scale linearly but are not very accurate. These computational methods have had a tremendous impact on practical chemistry - the 1998 Nobel Prize in Chemistry was awarded to the authors of many of these algorithms.
Despite the breadth of existing computational quantum mechanical tools, the problem of efficiently representing information required the development of a new method. It is no coincidence that only tens of thousands of electrons are involved in the largest modern quantum chemical calculations (we are talking about the most approximate methods), while classical methods of chemical calculations, for example, molecular dynamics, allow one to handle millions of atoms. It is not difficult to describe the state of a classical system - you just need to track the position and momentum of each particle. Imagining the state of a quantum system is a much bigger challenge. We have to assign a probabilistic value to each possible configuration of electron positions. This information is encoded in a wave function,allowing you to assign a positive or negative number to each electron configuration, and the squared wave function gives the probability with which the system can be found in such a configuration. The space of all possible configurations is colossal - if you tried to imagine it as a grid with 100 points in each dimension, then the number of possible configurations of electrons for a silicon atom would be greater than the number of atoms in the universe!
This is where deep neural networks come in handy. In the past few years, tremendous advances have been made in representing complex probability distributions with high dimensionality using neural networks. It is now known how to effectively train such networks with the expectation of their scalability. We assumed that since these networks have already proven their agility in training functions with many dimensions in solving problems from the field of artificial intelligence, maybe they will work for representing quantum wave functions. We were not the first to have such thoughts - other researchers, in particular, Giuseppe Carleo and Matthias Troyerdemonstrated how modern deep learning is applicable to solving idealized quantum problems. We wanted to use neural networks to tackle more realistic problems in chemistry and solid state physics, which meant we needed to take electrons into account in our calculations.
There is only one caveat when working with electrons. Electrons must obey the Pauli exclusion principle, that is, two electrons cannot simultaneously be in the same place. The fact is that electrons are elementary particles from among the fermions that make up the majority of the first bricks of matter, in particular, protons, neutrons, quarks, neutrinos, etc. Their wave function must be antisymmetric - if you swap two electrons, the wave function is multiplied by -1. Thus, there is a zero probability that two electrons will sit on top of each other, since the probability of this (and the corresponding wave function) is equal to zero.
Therefore, it was necessary to develop a neural network of a new type, which would be antisymmetric with respect to the input entering it. We named it Fermionic Neural Network or FermiNet. In most quantum chemical methods, antisymmetry is introduced using a function called a determinant. The determinant is a matrix that has the following property: if you swap two of its rows, then the output is multiplied by -1, exactly like the wave function of fermions. You can take a bunch of one-electron functions, calculate them for each electron in your system, and then fit all the results into one matrix. In this case, the determinant of the matrix will be a truly antisymmetric wave function. The main limitation of this approach is that the resulting function - called the Slater Determinant - is not widely applicable.The wave functions of real systems are usually much more complex. Typically, large linear combinations of Slater determinants — sometimes millions or more — are taken to correct this problem, and then some simple corrections are made based on electron pairs. Even then, the system may not be accurate enough to calculate energies.

2 – . – , 1. 1 2 , , -1. .
Deep neural networks are often far superior in efficiency to linear combinations of basis functions when representing complex functions. In FermiNet, this superiority is achieved by introducing each of the functions into the determinant, the function of all electrons. This method is much more powerful than using one- and two-electron functions. FermiNet provides a separate information stream for each electron. Without taking into account any interactions between these flows, the network would be no more expressive than the usual Slater determinant. To do more, we average the information collected from all streams on each of the network layers and pass this information to each of the streams to the next layer. Accordingly, such flows have suitable symmetry properties to create an antisymmetric function.
Information on each of the layers in graph neural networks is aggregated in a similar way . Unlike Slater's determinants, FermiNet networks are universal function approximators , at least as long as the layers of neural networks remain wide enough. This means that if we can train these networks correctly, then they can produce an almost exact solution to the Schrödinger equation.
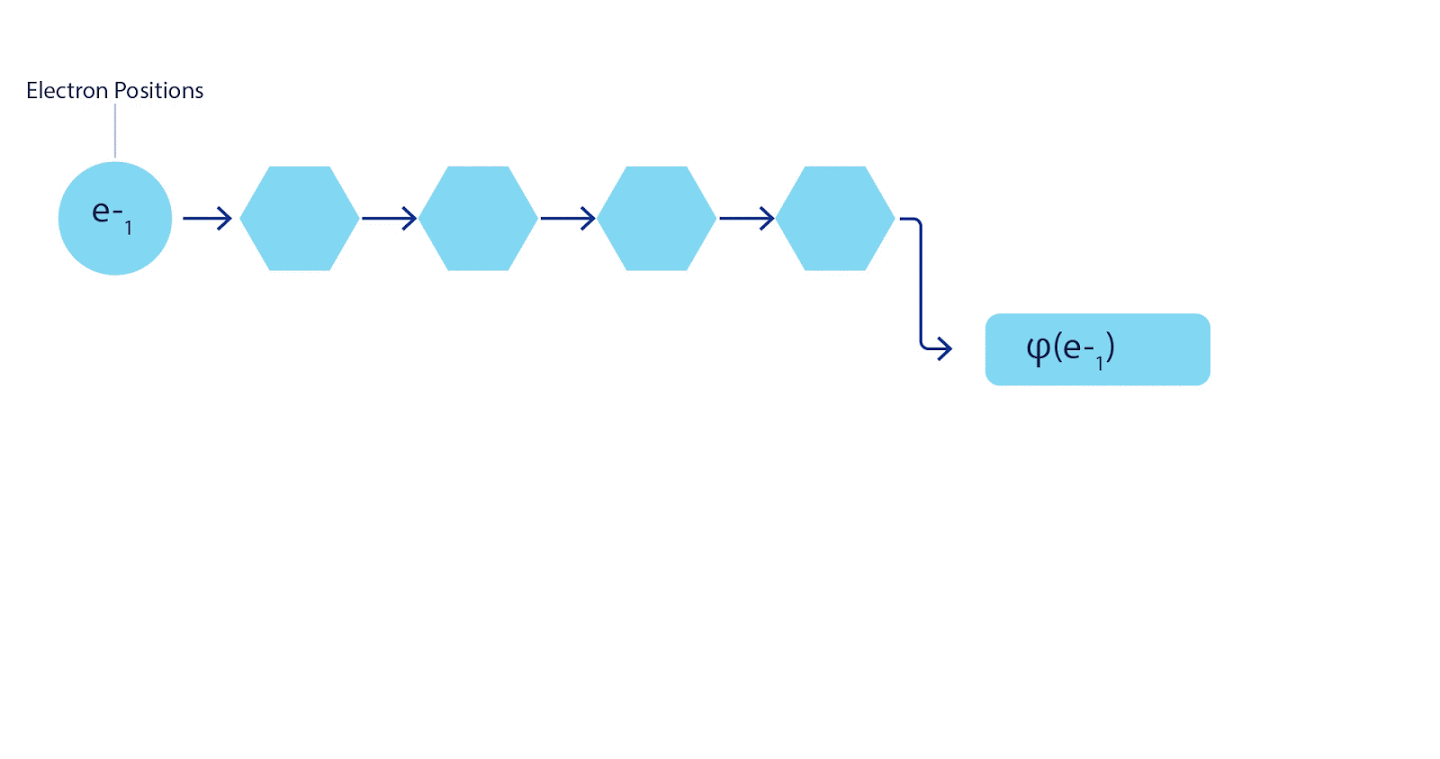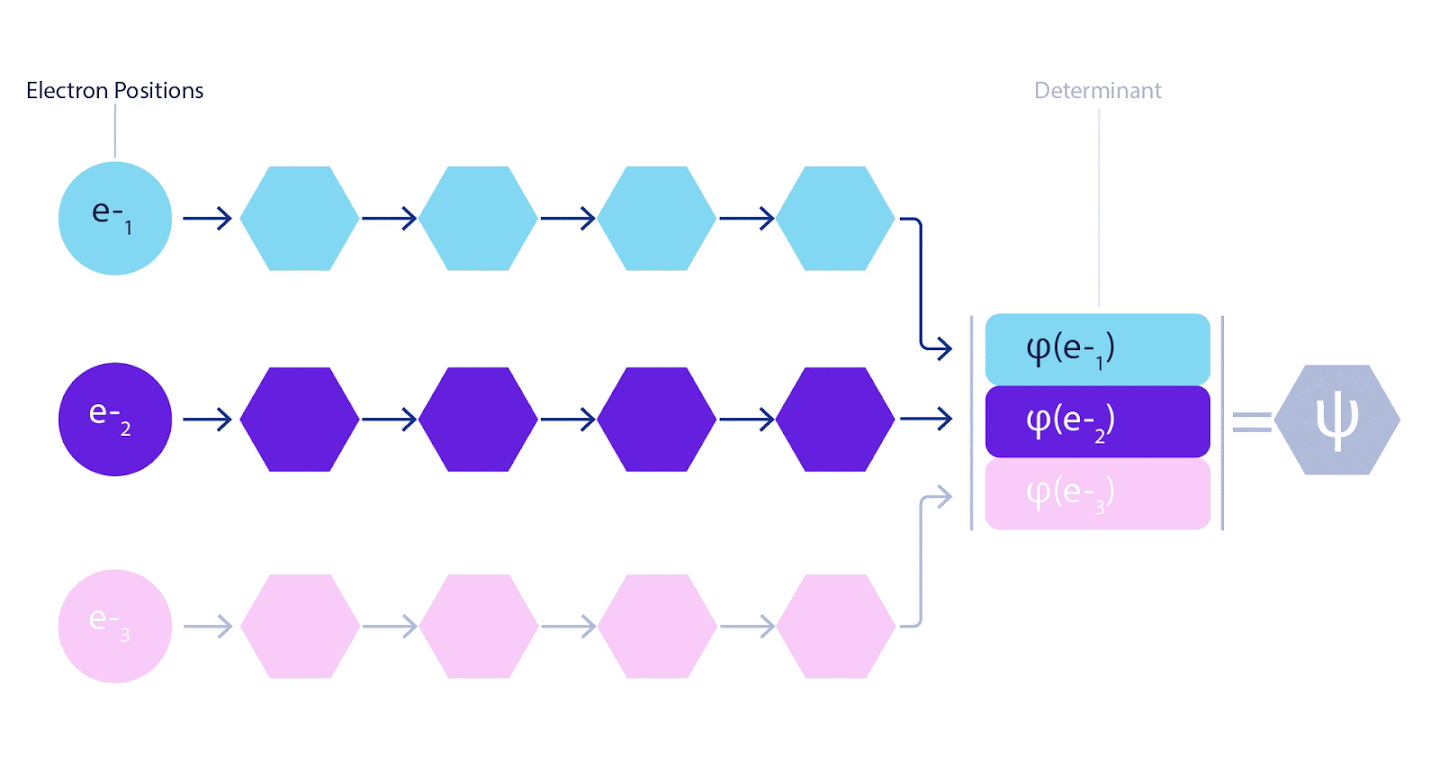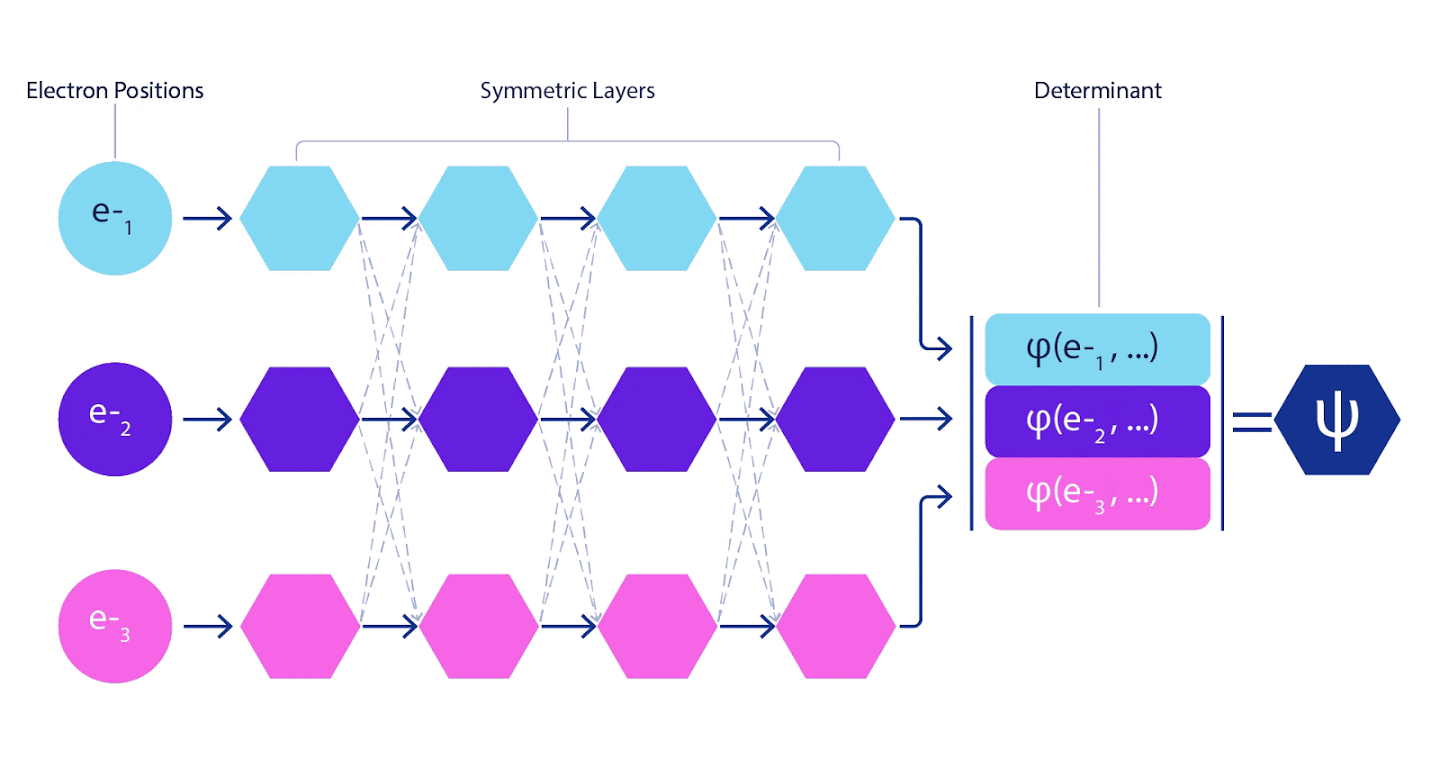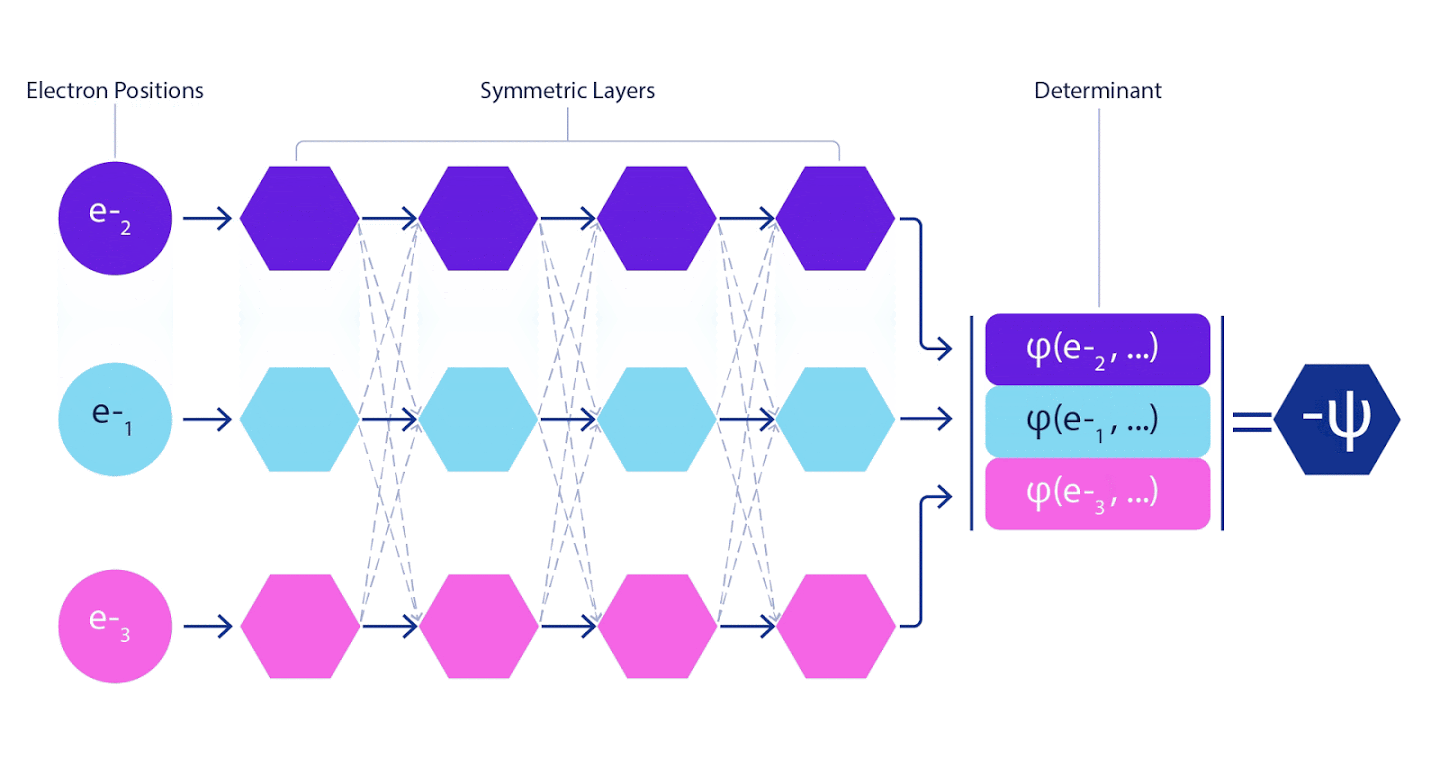
3 – FermiNet. (, ) . FermiNet , , , . , - -1.
We customize the FermiNet network, minimizing system energy. To do this accurately, we would need to calculate the wave function in all possible electron configurations, so we would have to do this approximately. Therefore, we take a random sample of electron configurations, calculate the energy locally for each variant of electron ordering, and minimize this energy, not the true one. This method is called "Monte Carlo", as it is a bit like the actions of a casino player who rolls the dice over and over again. Since the squared wave function makes it possible to observe some configuration of particles at any location, it is most convenient to generate samples of the wave function itself - in essence, simulating the act of observing particles.
While most neural networks are trained on some external data, in our case the neural network itself generates the input that goes into it for training. The situation is a bit like pulling yourself out of a bog by your hair, and means that we don't need any training data other than the positions of those atomic nuclei around which electrons dance. The basic idea, known as the Variational Quantum Monte Carlo Method (or VMC for short), has been around in science since the 1960s and is generally considered a cheap but not very accurate way to calculate the energy of a system. By replacing simple wave functions based on Slater determinants with functions from FermiNet, we managed to radically improve the accuracy of this approach on all systems we considered.
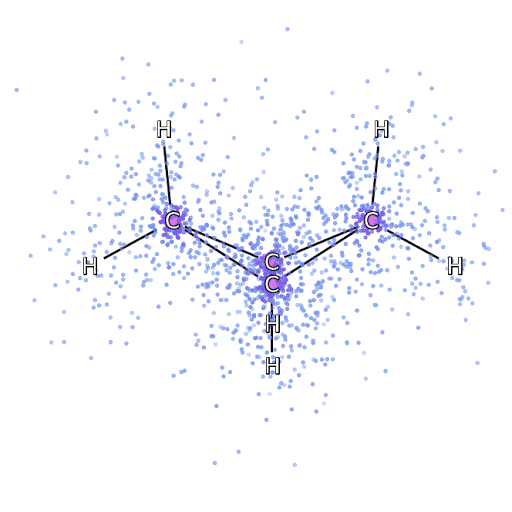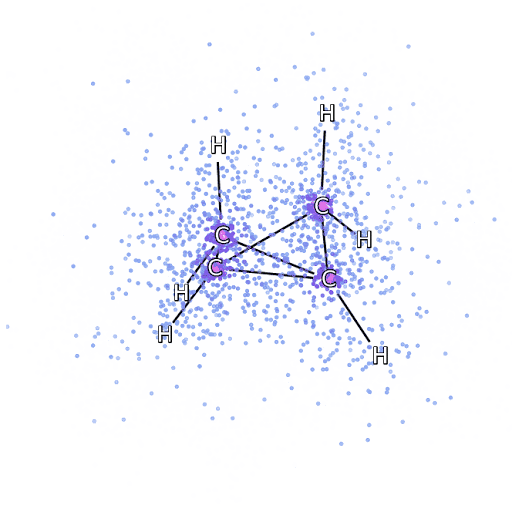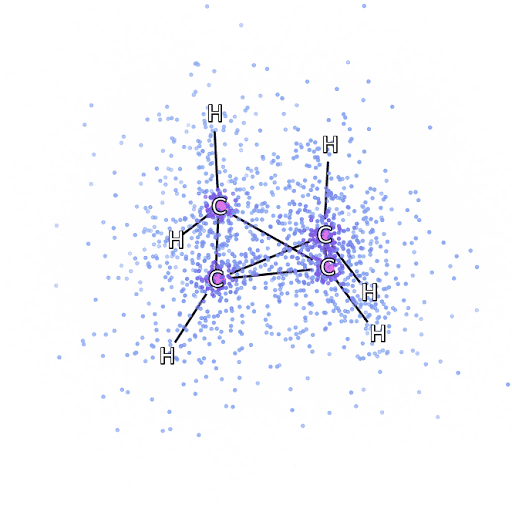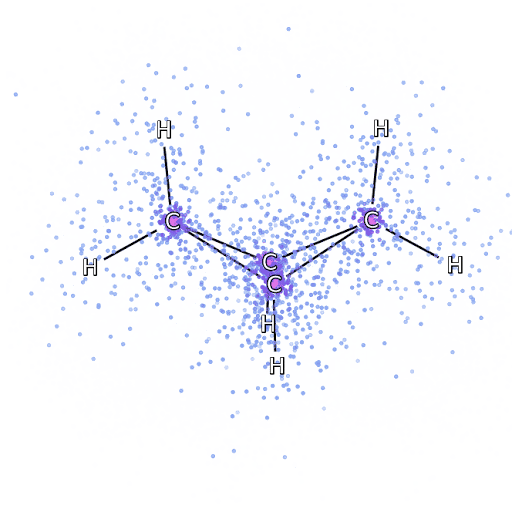
4 – , FermiNet, .
To make sure that FermiNet is truly a breakthrough in its subject area, we started by examining simple, well-studied systems, for example, atoms from the first row of the periodic table (from hydrogen to neon). These are small systems - 10 electrons or less - so they lend themselves to research using the most accurate (but exponentially more complex) methods. FermiNet far outperforms comparable VMC calculations, and can often cut error in half or more compared to exponentially scalable calculations. In larger systems, methods that become more complex exponentially become inapplicable, so we used the coupled cluster method as a reference. This method works well on molecules with stable configurations, but slips when the bonds are stretched or damaged,and such factors are critical to understanding chemical reactions. While it scales much better than exponentially, the connected cluster method used in this study still works as best as possible with medium-sized molecules. We applied FermiNet to ever larger molecules, from lithium hydride to bicyclobutane - it was the largest system we looked at, with 30 electrons. On the smallest molecules, FermiNet captured an astounding 99.8% difference between the energy of bound clusters and the energy derived from a single Slater determinant. In the case of bicyclobutane, FermiNet still captured 97% or more of this correlation energy - a huge achievement for a supposedly "cheap but imprecise" approach.While it scales much better than exponentially, the connected cluster method used in this study still works as best as possible with medium-sized molecules. We applied FermiNet to ever larger molecules, from lithium hydride to bicyclobutane - it was the largest system we looked at, with 30 electrons. On the smallest molecules, FermiNet captured an astounding 99.8% difference between the energy of bound clusters and the energy derived from a single Slater determinant. In the case of bicyclobutane, FermiNet still captured 97% or more of this correlation energy - a huge achievement for a supposedly “cheap but imprecise” approach.While it scales much better than exponentially, the connected cluster method used in this study still works as best as possible with medium-sized molecules. We applied FermiNet to ever larger molecules, from lithium hydride to bicyclobutane - it was the largest system we looked at, with 30 electrons. On the smallest molecules, FermiNet captured an astounding 99.8% difference between the energy of bound clusters and the energy derived from a single Slater determinant. In the case of bicyclobutane, FermiNet still captured 97% or more of this correlation energy - a huge achievement for a supposedly "cheap but imprecise" approach.which was applied in the described study, everyone equally works as a maximum with medium-sized molecules. We applied FermiNet to ever larger molecules, from lithium hydride to bicyclobutane - it was the largest system we looked at, with 30 electrons. On the smallest molecules, FermiNet captured an astounding 99.8% difference between the energy of bound clusters and the energy derived from a single Slater determinant. In the case of bicyclobutane, FermiNet still captured 97% or more of this correlation energy - a huge achievement for a supposedly “cheap but imprecise” approach.which was applied in the described study, everyone equally works as a maximum with medium-sized molecules. We applied FermiNet to ever larger molecules, from lithium hydride to bicyclobutane - it was the largest system we looked at, with 30 electrons. On the smallest molecules, FermiNet captured an astounding 99.8% difference between the energy of bound clusters and the energy derived from a single Slater determinant. In the case of bicyclobutane, FermiNet still captured 97% or more of this correlation energy - a huge achievement for a supposedly "cheap but imprecise" approach.starting with lithium hydride and reaching bicyclobutane, it was the largest system that we considered, it has 30 electrons. On the smallest molecules, FermiNet captured an astounding 99.8% difference between the energy of bound clusters and the energy derived from a single Slater determinant. In the case of bicyclobutane, FermiNet still captured 97% or more of this correlation energy - a huge achievement for a supposedly "cheap but imprecise" approach.starting with lithium hydride and reaching bicyclobutane, it was the largest system that we considered, it has 30 electrons. On the smallest molecules, FermiNet captured an astounding 99.8% difference between the energy of bound clusters and the energy derived from a single Slater determinant. In the case of bicyclobutane, FermiNet still captured 97% or more of this correlation energy - a huge achievement for a supposedly "cheap but imprecise" approach.but imprecise "approach.but imprecise "approach.

Figure 5 is a graphical representation of the fraction of the correlation energy that FermiNet correctly captures when working with molecules. The purple bar marks 99% correlation energy. From left to right: lithium hydride, nitrogen, ethylene, ozone, ethanol, and bicyclobutane.
While coupled cluster methods work well with stable molecules, the real "cutting edge" of computational chemistry has to do with understanding how molecules stretch, twist, and break. When solving such problems, connected cluster methods often fail, so you have to compare the result with as many control samples as possible to make sure that the answer is consistent. In the framework of the described experiment, two control stretched systems were considered - a nitrogen molecule (N 2) and a hydrogen chain of 10 atoms (H 10 ). In the nitrogen molecule, the bond is especially complex, since 3 electrons from each atom participate in it.
The hydrogen chain, in turn, is interesting for understanding what properties electrons exhibit in materials , for example, to predict whether a given material will conduct electricity or not. In both systems, the connected cluster method worked well in equilibrium, but ran into difficulties when the bonds were stretched. Traditional VMC methods did not perform well across the entire range of examples. But FermiNet turned out to be among the best methods of all investigated, regardless of the link length.
Conclusion
We believe FermiNet is the beginning of great advances in the synthesis of deep learning methods and computational quantum chemistry. Most of the systems with which FermiNet has been reviewed so far are well understood and understood. But just as the first good results using deep learning in other subject areas have spurred a surge in further research and rapid progress, hopefully the same will happen with FermiNet, and ideas for new, even better neural network architectures will emerge. Already after the described work was posted on arXiv, other groupsshared their approaches to applying deep learning to solving problems that involve many electrons. In addition, we have just barely dug in computational quantum physics and plan to use FermiNet to solve complex problems in the field of materials science and solid state physics.
The scientific article is here , and the code can be viewed here . The authors would like to thank Jim Kinwin, Adam Kine, and Dominic Barlow for their help in preparing the drawings.