How four mathematicians solved the question of basic geometric shapes by creating a complete list of tetrahedra with rational angles using number theory methods.
All 59 tetrahedra with rational dihedral angles can be viewed from different sides by reference .
The tetrahedron is the simplest three-dimensional shape with flat sides. Its main properties have puzzled inquisitive minds even in the days of Plato and Aristotle. And in November 2020, the final proof was published , which reliably identified all existing special tetrahedra. In this work, mathematicians are answering the question of an ancient figure thanks to advanced technologies that make it possible to use a new method of finding solutions to certain equations.
“These are idealized mathematical objects that will always be with us, and now we know all of them,” says Martin Weissman of the University of California, Santa Cruz.
The tetrahedron has a triangular base and three triangular sides, forming a pyramid. Pairs of faces touch at the edges to form six dihedral corners.
The new proof defines all variants of the configuration of the tetrahedron, where each of the six dihedral angles has rational values, which means that each of them can be written as a fraction. It states that there are exactly 59 separate examples, as well as 2 infinite families of tetrahedra, satisfying this condition.
In fact, these tetrahedrons were discovered by mathematicians decades ago using computer search methods, but they did not know if there were any else. More broadly, they did not understand how to prove that there were no other similar tetrahedrons.
“They were found back in the 1990s, but it wasn't until 2020 that we were able to prove that the list was comprehensive,” said Kiran Kedlaya , a mathematician at the University of California, San Diego. Kedlaya is a co-author of the proof with Alexander Kolpakov of the University of Neuchâtel in Switzerland, Bjorn Punen of the Massachusetts Institute of Technology, and Michael Rubinsteinfrom the University of Waterloo.
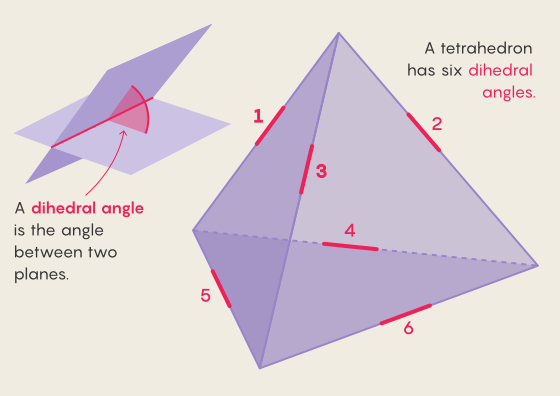
Samuel Velasco / Quanta Magazine
The problem of classifying tetrahedra with rational dihedral angles may seem simple, but it took years of accumulated mathematical knowledge to solve it, as well as computing power that was not available even ten years ago.
“You can't get that kind of result just by playing with a pen and paper. They have developed very sophisticated methods, ”says Marjorie Seneschal of Smith College.
There are almost no drawings in the 30-page proof. Instead, the logic is based on solving a polynomial equation in which the coefficients and variables are raised to a power, for example, y = 3x 2+ 6. Of course, the equation considered in the proof is much more complicated.
"Most of the work is based on number theory, but geometry lies on the surface," says Kedlaya.
The connection between geometry and number theory gave mathematicians a clue, but they had to work hard to develop this idea, because it is very difficult to find special solutions to complex equations and prove that you found them all. Mathematicians don't know how to do this for most equations.
“There is no one-size-fits-all method that always works. You can almost never solve an equation, ”says Peter Sarnack of the Institute for Advanced Study.
Only in this case, the mathematicians succeeded! By discovering a new method for finding solutions to polynomial equations, they answered the basic question about geometric shapes and may have made it easier to find solutions to other equations in the future.
Testing tetrahedrons
The question of defining all tetrahedra with rational dihedral angles (rational tetrahedra) was first formally formulated by John Conway and Antonia Jones in a 1976 paper .
They wanted to find tetrahedrons that could be cut and assembled into a cube of the same volume, a property known as scissor-congruence. In their work, they developed reasoning going back to 1900, when David Hilbert proposed 23 problems that guided mathematical research in the 20th century. His third problem is related to the following question: are pairs of three-dimensional figures of equal volume scissors. It was soon proved that this was not the case, but it turned out that all rational tetrahedra are congruent to the cube.
“Conway and Jones asked the question of rational tetrahedra as a special case of a much more complex issue of classification of tetrahedra,” said Kedlaya.
These are idealized mathematical objects that will always be with us.
Martin Weissman, University of California, Santa Cruz.
They were able to sketch a method for finding these tetrahedra: solving a specific polynomial equation. Their equation contains six variables corresponding to the six dihedral angles of the tetrahedron, and has 105 terms reflecting the complex relationship of the dihedral angles of the tetrahedron with each other. For comparison, imagine a triangle, its three interior angles are connected within a simple polynomial, consisting of only three members: a + b + c = 180 degrees.
The polynomial equation identified by Conway and Jones also has infinitely many solutions that correspond to infinite configurations of possible tetrahedra. Conway and Jones said that in order to define tetrahedra with all rational dihedral angles, mathematicians need to find a special class of solutions to the equation that exactly correspond to rational tetrahedra.
They themselves did not know how to find a solution, but they were sure that it could be done: "It is likely that an ordinary tetrahedron ... whose dihedral angles are rational, can be found using our methods."
More than 40 years later, four mathematicians have confirmed their assumption.
Roots from one
Conway and Jones' strategy is quite common among mathematicians who often look for special types of solutions when studying polynomial equations. These can be solutions in the form of integers or rational numbers. Or, as in this case, it can be solutions with the elegant name “roots from one”.
Most roots of one do not appear on the normal number line. Instead, they are among complex numbers like 3 + 4i, which have a real part (3) and an imaginary part (4). The roots of unity serve as solutions to polynomial equations and have a special algebraic property: raising them to a certain power gives 1. Moreover, they have an elegant geometric representation: they all lie on the unit circle in the complex plane.
To solve the Conway-Jones polynomial equation, you must assign complex numbers to all six variables to make the 105-term equation true. The variables do not literally represent the actual angle measurements, but replace the complex numbers associated with the cosines of the angles. Conway and Jones noticed that rational tetrahedrons will correspond to solutions of a polynomial in which all variables are roots of unity.
“Six angles become six points on the unit circle, and these complex numbers are needed to satisfy the polynomial equation,” Weissman said.

Samuel Velasco / Quanta Magazine
However, knowing this correspondence is not as useful as it might seem. Finding solutions is one thing. And proving that you have found them all is a completely different and much more difficult task.
In 1995, two authors of a new work, Punen and Rubinstein, actually found all tetrahedra with rational dihedral angles, as it turned out in the end. In fact, they guessed the way to find them by substituting combinations of six rational numbers into the equation.
“You can just try to take six rational numbers and plug them into the equation,” Poonen said. “The problem is that only solutions can be found this way. But he does not make it clear whether all possible options have been found. "
Search for every solution
In their new work, four mathematicians proved that the list of tetrahedra with rational angles found by Punen and Rubinstein 25 years ago was complete and no other examples would be discovered.
Their collaboration began in March 2020 after Poonen heard in one talk about the related work of Kedlai, co-authored by another mathematician. They looked for roots from the unit of another polynomial to solve another classification issue. Poonen immediately realized that this had something to do with his previous unfinished study of tetrahedrons.
“Bjorn was very interested in my work,” said Kedlay. "He said, 'Wait, that's exactly what I needed in the 1990s.'
Bjorn Punen wrote a letter to Kiran Kedlae describing the problem of finding rational tetrahedrons. His short letter ended on an optimistic note. “I got pretty far on this issue back in the 1990s [with Michael Rubinstein], and I think it can be completed with a lot of human and computer effort.
In 2020, Kiran Kedlaya, Michael Rubinstein, Bjorn Punen and Alexander Kolpakov invented a new way to solve equations and in doing so found all rational tetrahedra.
After this letter, Kedlai turned to Kolpakov, who also used roots from unity to classify the types of geometric shapes. At the same time, Poonen contacted his then co-author Rubinstein. Having created a team, they quickly got to work.
“We organized pretty regular meetings, probably two hours a week for several months,” Kedlaya said. And when they started compiling a complete list of the roots of unity for the Conway-Jones polynomial, they had a very broad idea of where to look for them.
They knew that solutions had to be below some very large number, an upper bound. But the border was so great that there was no question of exploring all the possibilities below it.
“These six-variable boundaries are terrifying. Without fundamentally new ideas, the solution to this problem is beyond the realm of the possible, ”Sarnak said.
Four mathematicians made the equation solvable through two major innovations.
First, they lowered the upper bound. In their new paper, they proved that one complex polynomial equation representing tetrahedra can itself be represented as several simpler polynomials.
“We're moving from one equation with six variables to a set of hundreds of simpler equations,” Kedlaya said.
They proved that all the roots of unity of these simpler polynomials lie below the upper bound, which is much smaller than the vast and unexplored upper bound associated with a more complex polynomial. The correspondence between simpler equations and complex ones means that finding roots of one for the former will result in roots of one for the latter. Unfortunately, even this smaller interval was still too long for them to explore all possible options.
You can't get this kind of result just by playing with a pen and paper.
Marjorie Seneschal, Smith College
The second innovation of the authors consisted in the development of a clever way of searching in this smaller interval. They knew that solutions have a certain symmetric structure, which means that if there is a solution in one part of the interval, there must be a solution in the other part of the interval.
This allowed them to develop new algorithms that used this structure to search more efficiently. Plus, they used these algorithms on much more powerful computers than Conway and Jones had when they first proposed using roots from 1 to solve a problem.
“It turns out we had to redesign [Conway and Jones's] strategy a bit with 40 years of additional knowledge and more powerful computers,” Kedlay said.
The new algorithms tested all possible combinations of solutions in a narrower interval. On the basis of this exhaustive definitive search, the authors finally proved that there are only 59 separate examples of tetrahedra with rational dihedral angles and two infinite families of tetrahedra (precisely those that Punen and Rubinstein had encountered decades earlier). Tetrahedrons in each infinite family differ in one parameter, offering endless options for increasing the size of some angles and decreasing others, while keeping all dihedral angles rational.
In this exploration, everyone will find something for themselves.
For mathematicians interested in identifying the roots of the unit of polynomial equations, the article offers a new convenient way to find them. In particular, the methods used by the authors to reduce a complex Conway-Jones polynomial to many simpler polynomials are likely to be applied to other complex polynomial equations that cannot be solved directly.
“This work suggests that many other problems that seemed insurmountable could possibly be solved with such ideas,” Sarnak said.
And for those mathematicians and everyone else who like completeness, the article gives a new and perfect answer: here are all the tetrahedrons that you can only dream of.
“This is a great achievement,” said Sarnak.