Quick double comparison

Yesterday there was an article about fast parsing of doubles, I went to the blog of its author, and found another interesting trick there . When comparing floating point numbers, special attention has to be paid to NaN (eight years ago I wrote about them in more detail); but if the numbers being compared are certainly not NaN, then they can be compared faster than the processor does!



It is very simple to compare positive doubles: normalization guarantees us that of numbers with different exponents, the greater is the one whose exponent is greater, and of the numbers with the same exponent, the greater is the one whose mantissa is greater. The IEEE 754 standard has carefully placed the exponent in the most significant bits, so that positive doubles can be compared simply as int64_t.







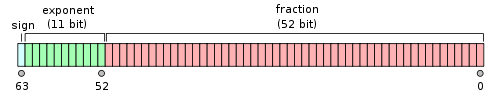
Negative numbers are a little more complicated: they are stored in direct code , while int64_t is stored in complementary . This means that in order to use an integer comparison, the lower 63 bits of a double must be inverted (this will result in -0. <+0., Which does not correspond to the standard, but in practice does not present a problem). An explicit check for the most significant bit and a conditional branch would destroy all the benefit of jumping to an integer comparison; but there is an easier way!

inline int64_t to_int64(double x) {
	int64_t a = *(int64_t*)&x;
	uint64_t mask = (uint64_t)(a >> 63) >> 1;
	return a ^ mask;
}

inline bool is_smaller(double x1, double x2) {
	return to_int64(x1) < to_int64(x2);
}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

a>>63



fills all 64 bits with copies of the sign bit, and then >>1



clears the most significant bit.



Daniel Lemire's blog post has slightly different code (of the same computational complexity), but my version retains the useful property that to_int64(0.) == 0