It is my deep conviction that all tasks are divided into two types: simple and complex. Simple problems have simple solutions (even if they require a certain amount of special knowledge to find them), but there are no complex problems in mathematics. To illustrate this, I'll show you an amazingly simple proof of the statement in the title of the post. One picture.
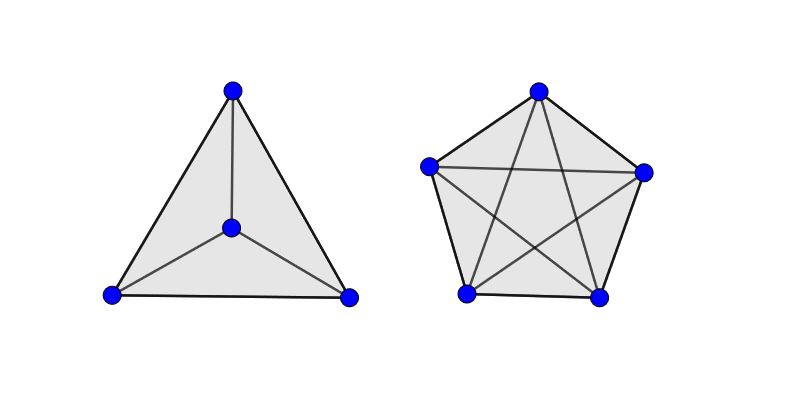
To begin with, what is shown in the picture? There is no unambiguous mathematical answer to this question: from a geometrical point of view, these are orthogonal projections of a five-cell on the Coxeter plane A 2 and A 4 , and from the point of view of graph theory - diagrams K 4 and K 5 .
, , R(5,5) : , 39 4 , 43 — , . , , , .
, — . , ; : - , . , .
:
( ) — (V, E) ( ), E ⊆ {{v1, v2} | v1, v2 ∈ V, v ≠ v2}.
— , , — , .
— , , . , 10-, 10 .
— , . ( ), ; , .
Kg — g , , .
— , .
— , .
— ( ).
() R(n,m) — , n , m .
:

.
: , A,B,C,D , AB, AC, BC, CD — .

. : , — . : AB CD , .
.

( ), , 36 ( ) R(3,9), : R(5,5)=45, R(4,6)=36, R(4,7)=49.
:
, «» . , . , «» — .
10- 45 , K45. :

, 10 , 16. , 43 ( 150 , ).

, , - . ; , , .
Happy end? ! 43 , . , . !
. , : R(9,9)=432+43+1=1893 , ( , , ) ( — ). .

R(3,3) 5 , R(5,5) , 43=62+6+1. , R(5,5) 9, R(9,9) . . , , . , R(9,9) 631 3 , .
, .
.
:
TAKEUCHI, Kisao. Arithmetic triangle groups. J. Math. Soc. Japan 29 (1977), no. 1, 91--106.
, , , , , , « », — . , , , . .
: - . — , , « », «». , , — . . « , , , , , , , , , , , , , ?» — . , , . , , « , » , — , ctrl+c/ctrl+v .
? , . , , , . , ? . : , - — , . , (!!!) - , — — .
, — .
: K8? « » , , , . .
, R(5,5)=43 :
K4 , CMYK, — .
6 K6, 15 , 15 .
K4 K8, 28 , 28 .
15 .2 28 .3 K43, 903 4 .
Squeak a little with your brain on the subject of color temperature or invite some artist to give a lecture on warm and cold shades, into two sets of which (black and white) and you need to break the edges of the resulting graph.
Profit!
Thank you for reading, that's all for today. Always yours, Malcheg-Zaycheg.