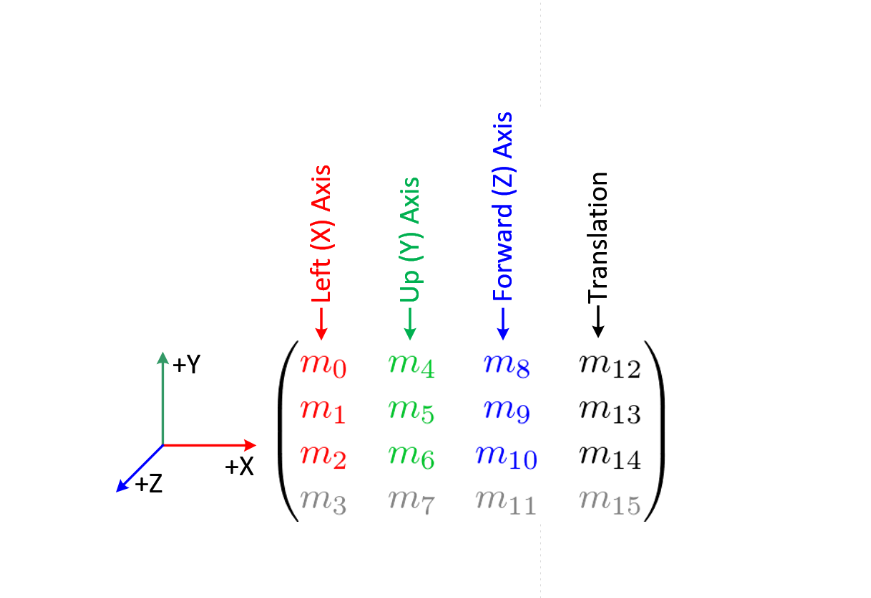
👰🏽 🤞 👩🏻 Why are we transforming 3D vectors with 4x4 matrices? 🥠 🛬 🤹🏻

Why not a 3x3 matrix? Why is everything arranged in a 4x4 matrix exactly like this? Why is there the last line filled with zeros and one at the end? I asked these questions the day before, decided to investigate the issue and tell what I found out.

In the article, we will be interested only in affine transformations, and in particular rotation, scaling and movement, which are actively used in graphics programming and game development in general.

: . , , , (A⋅x). , , , (+b).

T, x

$T (\ vec {x}) = A \ vec {x} + \ vec {b}$

, b x . x x', :

$\ begin {array} {ll} A \ rightarrow [a] \ rightarrow a, \\ \ vec {b} \ rightarrow (b) \ rightarrow b, \\ \ vec {x} \ rightarrow x, \\ T (x ) \ rightarrow x '\ end {array}$

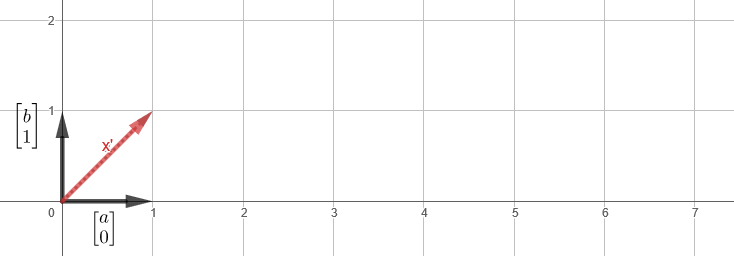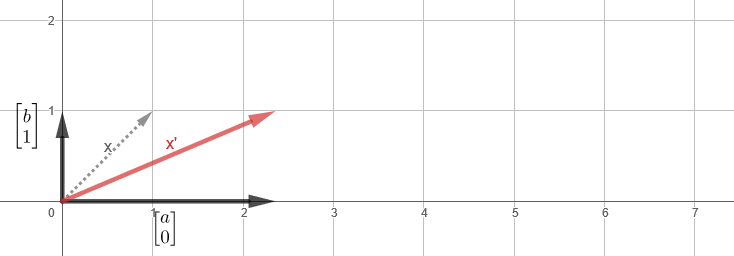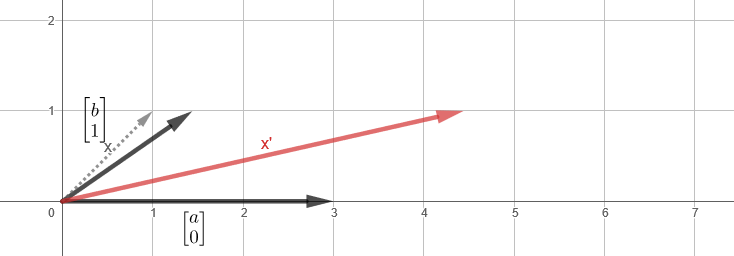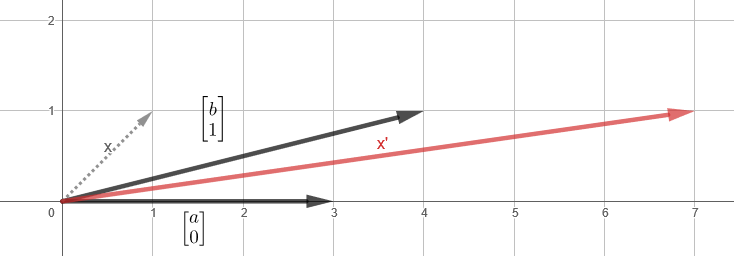
x ( ), b ( ).

, , . M, :

x' = 3x + 4 (3x +4 ) .

$\ begin {array} {ll} Mx = 3x + 4 \\ M = (3x + 4) / x \\ M = 3 + (\ frac {4} {x}) \ end {array}$

, ( 3x [3]), (x+4) , M x.

:

+4 +4y, y, x ,

$x '= 3x + 4y \\ y' = \ _x + \ _y$

2x2, x' = 3x+4 x, . . , .

$\ begin {bmatrix} x '\\ y' \ end {bmatrix} = \ begin {bmatrix} 3 & 4 \\ \ _ & \ _ \ end {bmatrix} \ begin {bmatrix} x \\ y \ end {bmatrix }$

2x2 , , - y, +4y , +4, x :

$\ begin {bmatrix} x '\\ y' \ end {bmatrix} = \ begin {bmatrix} 3 & 4 \\ \ _ & \ _ \ end {bmatrix} \ begin {bmatrix} x \\ 1 \ end {bmatrix } \ rightarrow \ begin {array} {l} x '= 3 \ cdot x + 4 \ cdot 1 \\ y' = \ _ \ cdot x + \ _ \ cdot 1 \ end {array}$

, , , , 3x+4 x' - y' y' ,