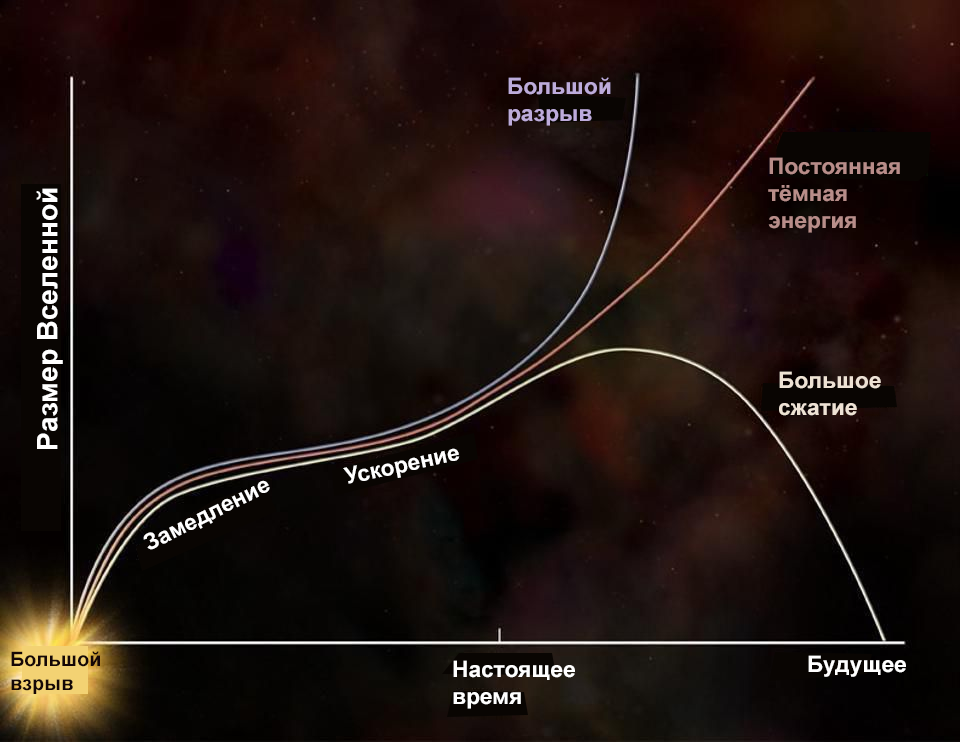
In the distant future, the Universe can expect different variants of fate , but if dark energy is really constant - as all the data testify to this - then its development will continue to follow the red curve. This curve will lead the Universe to a variant of heat death. However, dark energy does not have to be a cosmological constant.
One of the most mysterious components of the universe is dark energy.... To be honest, it shouldn't have been there at all. Earlier, we quite logically assumed that the Universe is balanced, and that its expansion is opposed by the forces of gravity acting on everything in it. If gravity wins, the universe will collapse again. If the expansion wins, everything will fly into oblivion. However, observations made after 1990 suggest that expansion is not just gaining - distant galaxies are receding from us at an ever-increasing rate. However, can this be called a new idea, or is it just a resurrection of what Einstein once called his greatest mistake: the cosmological constant ? This question is asked by our reader:
Einstein's cosmological constant and dark energy the same thing? Why did the term "dark energy" eventually replace the original term "cosmological constant"? Are they identical or not, and why?
There are several questions here. Let's go back to Einstein's original idea, the cosmological constant.

Today we know that a significant proportion of galaxies other than the Milky Way are spiral-shaped. All the spiral nebulae we've studied since the 1920s are other galaxies. However, in Einstein's time this was far from obvious.
It must be remembered that when Einstein worked on the theory of gravity, which was supposed to replace and supplant Newton's law of universal gravitation, we knew little about the universe. Of course, astronomy has been around for thousands of years, and telescopes have been around for much of that time. We measured stars, comets, asteroids, nebulae. We have seen the birth of new and supernovae. We have discovered variable stars and atoms. We found interesting structures in the sky - spiral and elliptical.
But we didn't know that these spirals and ellipses were independent galaxies. This idea was only the second most popular; the leading opinion was that these are certain entities (possibly forming stars) located inside the Milky Way, which represented the entire universe. Einstein was looking for a theory of gravity that could be applied to everything - including the entire known universe.
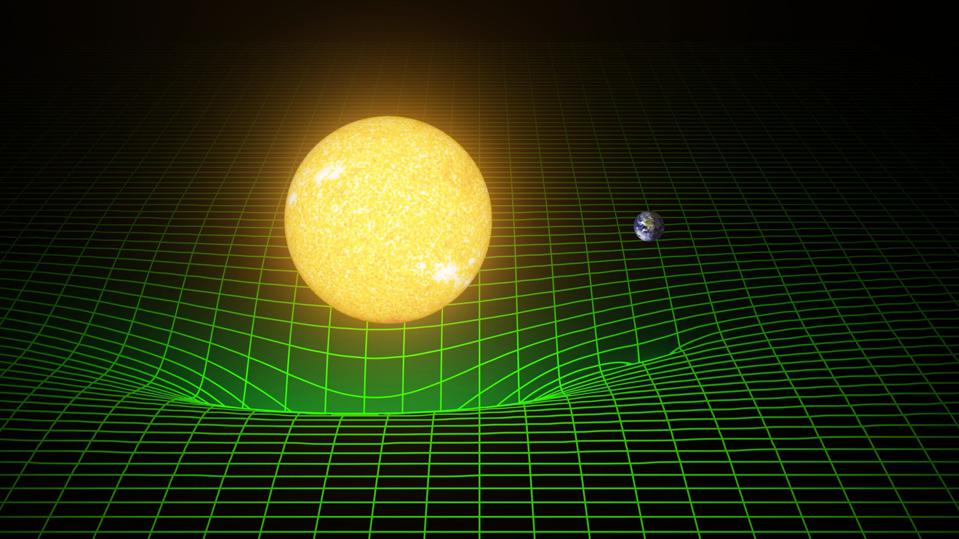
The gravitational behavior of the Earth near the Sun is better explained not by the presence of an invisible gravitational attraction, but by the free fall of the Earth in space curved by the Sun. The shortest distance between two points is not a straight line, but a geodesic - a curved line determined by the gravitational deformation of space-time.
The problem became apparent when Einstein was able to formulate his greatest achievement: general theory of relativity (GR). Rather than relying on masses infinitely fast acting on each other over infinite distances, Einstein presented a completely different concept. First, since space and time were not absolute, but relative for each of the observers, the theory had to make identical predictions for all observers: as physicists say, to be " relativistically invariant"And this meant that the separate concepts of space and time had to be woven into a single four-dimensional fabric of space-time. Gravitational effects were no longer propagating at infinite speed, but were limited by the speed of gravity, which, according to Einstein's theory, is equal to the speed of light.
Einstein's key breakthrough was the replacement of the masses attracting each other with the curvature of space-time, which affects both matter and energy. Curved spacetime dictated how matter and energy needed to move. And matter and energy at each moment of time tell the space how to bend. And this is how they affect each other - after each shift of matter and energy, the curvature of space changes slightly. Their changes are governed by the equations of general relativity.

Animation of the reaction of space-time to a moving mass in it. It allows one to imagine space-time not as a two-dimensional "fabric", but as a real object. Three-dimensional space is curved due to the presence and properties of matter and energy. The movement of several masses around each other causes gravitational waves.
If Einstein had stopped there, he would have launched the space revolution. On the one hand (so to speak, on the one hand of the equal sign in the equation) all the matter and energy of the universe. On the other hand, the curvature of space-time. It should end there - the predictions of the equation should tell you what will happen in the future.
And when Einstein solved these equations for a large distance from a small mass, he received Newton's law of universal gravitation. But when approaching the mass, corrections began to creep out - both explaining the previously unexplained deviations of the orbit of Mercury, and predicting that the light of stars passing by the Sun should deviate from a straight line. This is how the general theory of relativity was first confirmed in practice.
However, in another situation, another problem arose. If we assume that the universe is uniformly filled with matter, then from the equations it turns out that it is unstable. If it began to exist in static space-time, then it must collapse. To remedy the situation, Einstein invented the cosmological constant.
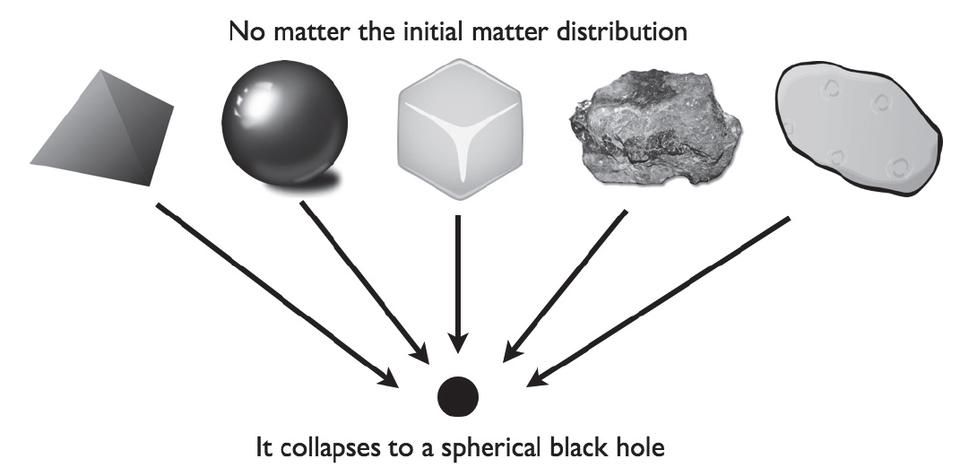
If the universe is not expanding, it can be filled with stationary matter of any kind, but it will always collapse into a black hole. In the context of Einstein's gravity, such a universe is unstable, and must expand.
We need to understand where the idea of the cosmological constant comes from. There is a powerful tool in mathematics that is ubiquitous in physics: the differential equation . It could be something as simple as Newton's law F = ma. This equation simply explains how certain quantities will behave in the next moment. After that moment has passed, they can be substituted into the same equation, and it again predicts what will happen to them the next moment.
A differential equation, for example, can tell what happens to a ball rolling down a hill. It tells what path it will take, how it will accelerate, how its location will change over time. By solving the differential equation describing the motion of a ball rolling down a hill, you can accurately plot its trajectory.
The differential equation will tell you almost everything you want to know about a ball rolling down a hill. But it cannot tell you one thing: how high the hill is. You do not know if this hill is located on a mountain plateau, whether it ends at sea level, or in the crater of an extinct volcano. Identical hills located at different heights will be described by the same differential equation.
, , . - . – , ? , .
A similar problem arises in calculus when you first learn to take the indefinite integral - the infamous "plus constant" that needs to be added at the end. Of course, general relativity is not one differential equation, but a matrix of 16 differential equations, 10 of which do not depend on each other. But a constant can be added to each of them in a certain way - and it became known as the cosmological constant. You may be surprised, but this is the only thing that can be added to general relativity without fundamentally changing the essence of the theory (except for another form of matter or energy).
BUT Einstein added the cosmological constant to his theory, not because it could be done, but because from his point of view it was preferable. Without adding a constant, his equations said that the universe should expand or contract, but nothing of the kind was noticeable. And instead of believing the equations, Einstein injected a constant into them to "fix" a seemingly broken situation. Had he listened to the equations, he would have predicted the expansion of the universe. Instead, the work of other scientists refuted Einstein's choice, and he himself abandoned the cosmological constant only in the 1930s, when the expansion of the universe was confirmed by observations.
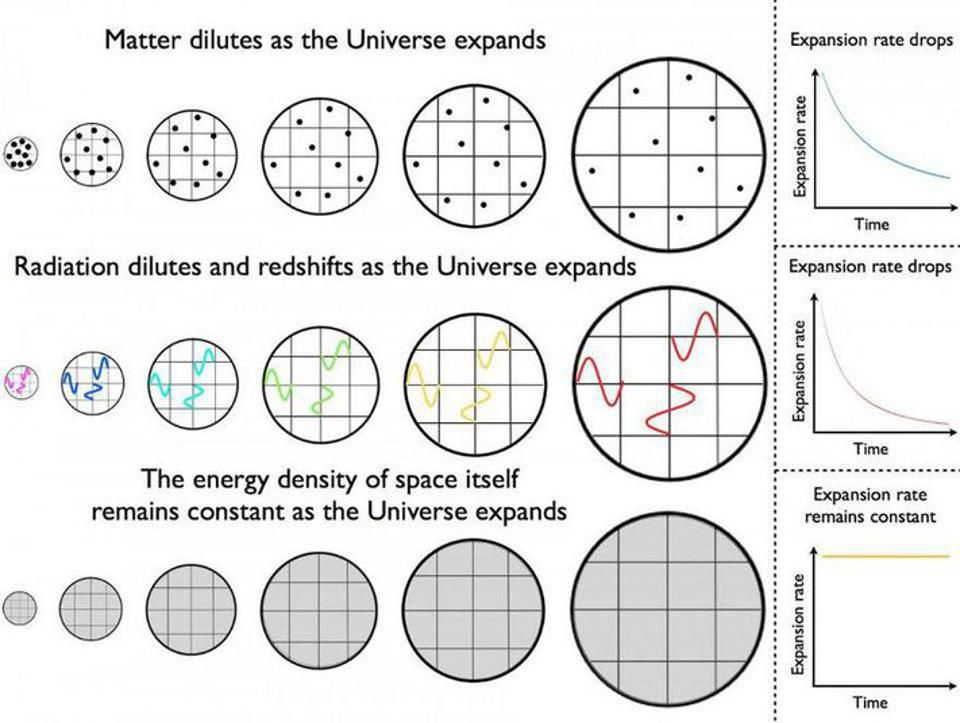
During the expansion of the Universe, ordinary and dark matter, as well as radiation, become less dense. However, dark energy and field energy during inflation are inherent in space itself. Therefore, the density of dark energy remains constant.
The problem is that the cosmological constant is not like the forms of energy we know. Take matter - there is a constant amount of its particles in the Universe. With the expansion of the Universe, it does not change, so its density decreases. If we take radiation, then not only the number of quanta is constant, but the radiation, traveling through the expanding Universe, is stretched from the point of view of an observer who will someday catch it. Its density decreases, and each quantum also loses energy over time.
But the cosmological constant is a constant form of energy inherent in space itself. It is as if the surface of the Earth was not at sea level, but would rise by several meters. Yes, this new height could simply be called "sea level", but this will not work with the universe. There is no way to find out the magnitude of the value of the cosmological constant - we simply assumed that it is zero. But this is not necessary - it can be any value, positive, negative, or zero.

Various components and contributions to the energy density of the universe, and their relative dominance. Radiation dominated matter for the first 9000 years, then matter began to dominate, and then the cosmological constant came out ahead. All other components are too few. However, dark energy may not be equivalent to the cosmological constant.
Extrapolating back in time to an earlier, hot, dense and shallow universe, we may not notice the cosmological constant. In the early stages, it was vastly superior to matter and radiation. It was only after the universe expanded and cooled that the density of matter and energy dropped enough for the cosmological constant to manifest.
That is, if it exists at all.
Dark energy may turn out to be a cosmological constant. And, indeed, taking into account all today's observations, it seems that this is so - the change in the rate of expansion of the Universe over time proceeds as the cosmological constant dictates. However, there are some errors here, so dark energy can, in principle, over time:
- increase or decrease,
- change the energy density,
- develop in some new complex way.
Although we have limitations on the values of dark energy over the past 6 billion years, we cannot call it constant with absolute accuracy.
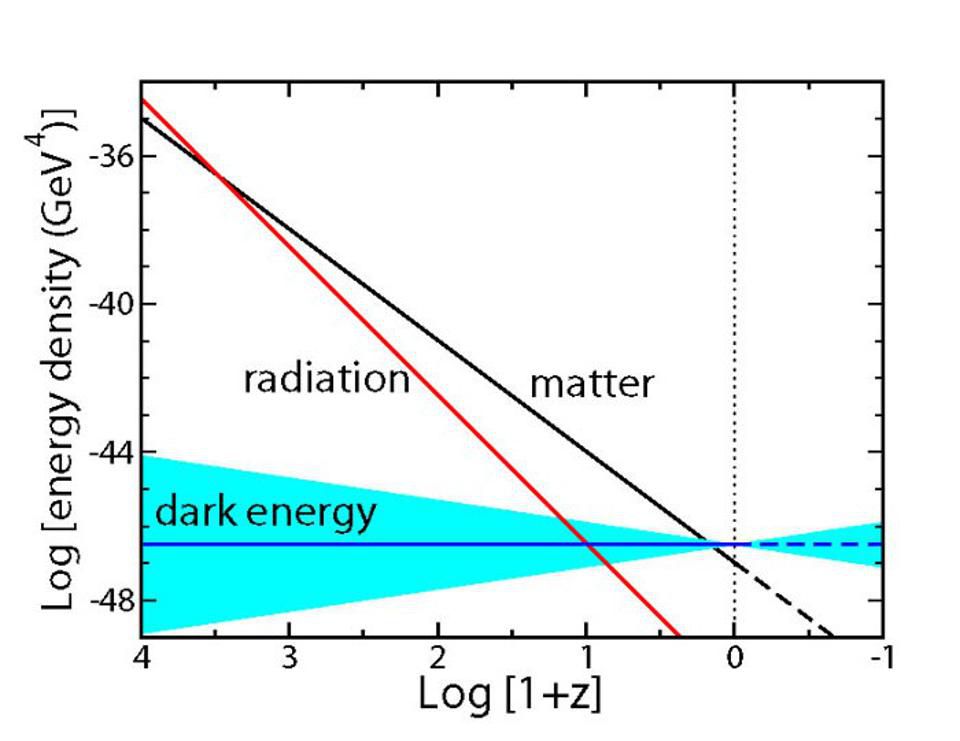
The densities of matter, radiation and dark energy are well known. However, for dark energy, there is still a lot of wiggle room in the equations. It can be constant, but it can also change over time.
We, of course, would like to know if it is constant or not. And we will find out, as is usually done in science - improving observations and conducting them consistently. The keys to this are large datasets, as well as probing the universe over a wide range of distances. After all, all the smallest details of the change in the rate of expansion of the Universe in time helps us to find out how the light traveling through the Universe changed. If dark energy is exactly equal to the cosmological constant, then its development will follow a certain curve. If not, then another, and we can see it.
By the end of the 2020s, we will have a huge and complex ground-based complex to observe the universe. All thanks to the observatory. Vera Rubinwhich will surpass the achievements of all existing instruments such as Pan-STARRS and Sloan Sky Survey . We will have a huge array of space observations thanks to the European Euclid Observatory and NASA's Nancy Roman Telescope - they will be able to see 50 times more detail than the Hubble Telescope. All of this new data will help us determine whether dark energy is indeed identical to what the cosmological constant predicts, and whether it changes over time.

, . , .
There is a great temptation - sometimes I am guilty of this - to combine these two concepts and consider that dark energy is just a cosmological constant. It is clear why one wants to do so - the cosmological constant is already a part of general relativity, and it does not need to be separately explained. Moreover, we do not know how to calculate the zero energy of empty space in quantum field theory, and it makes exactly the same contribution to the universe as the cosmological constant. Finally, all our observations are consistent with the fact that dark energy is a cosmological constant, and nothing more needs to be complicated.
However, it is from this that the extreme importance of the new dimensions follows. If we hadn’t bothered to carefully and accurately measure the universe, we would never have discovered the theory of relativity. We would not have discovered quantum physics, we would not have done most of the research that earned the Nobel prizes and propelled us into the 20th and 21st centuries. In 10 years, we will have data that will help determine whether dark energy differs from the cosmological constant with an error of 1%.

– . , ( WFIRST) – . , - . . 1%, .
The cosmological constant may turn out to be identical to dark energy, but this is not necessary. And even if they turn out to be the same, we will still want to understand why the cosmological constant behaves this way and not otherwise. In the coming year of 2021, it is important to remember that the answers to our deepest cosmic questions can be seen on the face of the universe. The only way to get them is to turn to physical reality itself.