Most likely, each of you has heard the term “affine transformations” at least once in your life. Indeed, everyone is constantly talking about them: "invariance to affine transformations", "augmentation using affine transformations", "affine transformations in computer graphics" and so on. However, not everyone can immediately answer a simple question: "Tell us what affine transformations are in simple words."
You can? Anyway, let's discuss this issue for a bit.
What is Affine Transformation?
Let's start with the classics - definition from Wikipedia.
Affine transformation (from Latin affinis "touching, close, adjacent") is a mapping of a plane or space into itself, in which parallel lines pass into parallel lines, intersecting lines into intersecting lines, crossing lines into intersecting lines.
Let's clarify a little.
First, what does “self-mapping” mean ? This means that if we were in space , then after education we must remain in it. For example: if we applied some kind of transformation to a rectangle and got a parallelepiped, then we left
in
. But if we got another rectangle from the rectangle, then everything is fine, we mapped the original space into ourselves. Formally it is described as follows: "transformation
maps space
to
". If written using formulas
.
-, « »? , , . , . , . , . - .
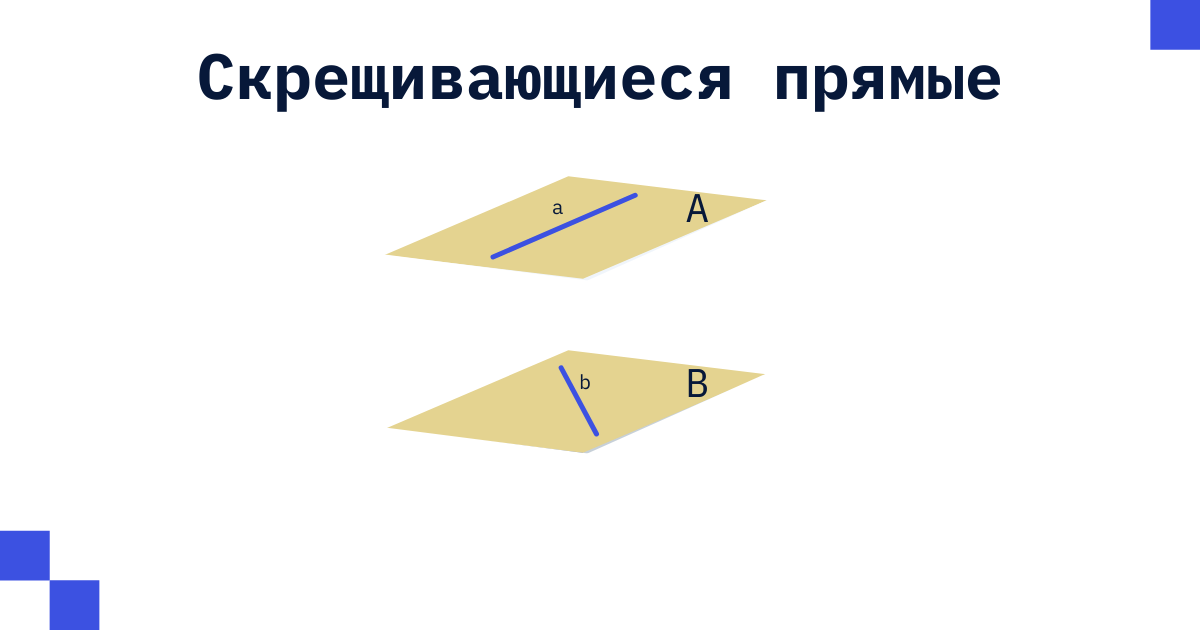
, - . , : . , 2 . , . , - , .
, - .
( ).
, , .
, , , , .
, « ». .. - , - .
- , - . : - . , ( , ).
, . , .
. -
.
:
, :
: , , ..
.
-
,
- ,
.
, ,
- .
, . .
- ? .
.
, :
:
? , - . .. . .

-
:
:
, , , 1 , 1. .
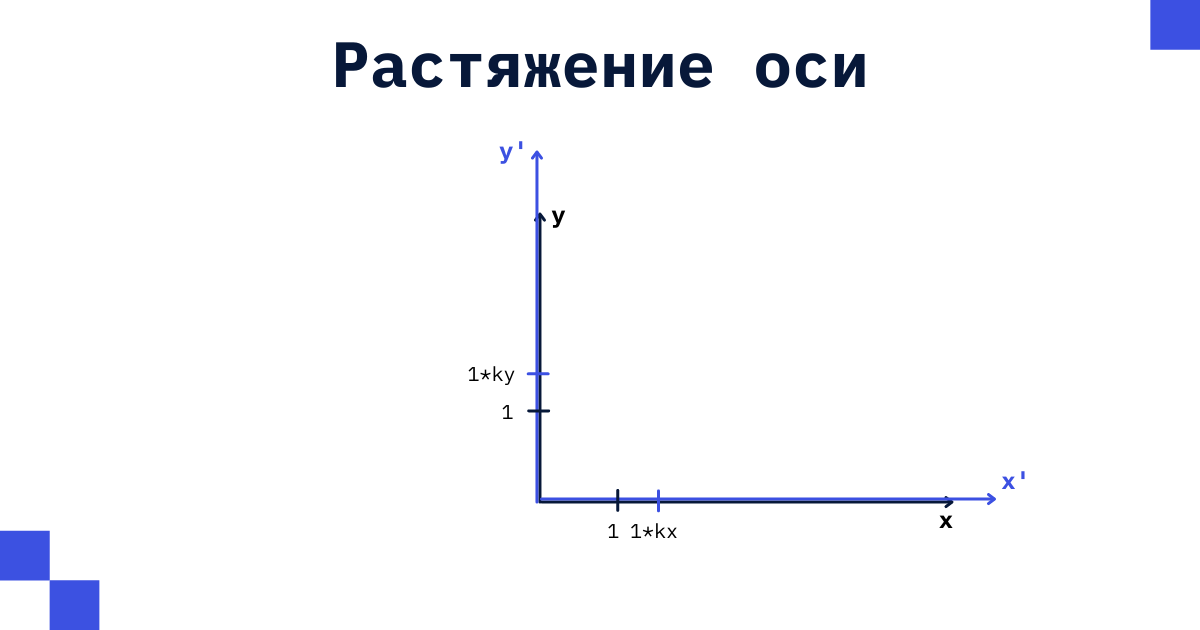
, -1,
1. ? ,
.
.
(..
).
,
.
, :
, . , , .

This short article will allow you to feel a little more strongly the "insides" of affine transformations (we hope so). After reading it, try to answer the question that we posed at the very beginning - "Tell us what affine transformations are in simple words." Can you now?
PS By the way, it would be nice not to take our word for it and check it ourselves - and the matrices that we used are definitely non-degenerate? Maybe we did something illegal at all? ...