Have you ever wondered what life would be like if the Earth were not a sphere, but had a different shape? We take for granted the smooth running of our planet through the solar system and the slow sunsets that we can enjoy thanks to the Earth's rotational symmetry. In addition, the spherical Earth allows you to determine the fastest way to get from point A to point B: just walk in a circle that goes through these two points and cuts the sphere in half. We use these shortest paths, called geodetic paths, for planning aircraft routes and calculating satellite orbits.

But what would happen if we lived in Cuba? Our world would rock more, horizons are curved, and the shortest path from point A to point B is harder to find. You may not spend a lot of time to imagine your life on a cube, but mathematicians will: they study what our travels would look like on a variety of shapes. And the recent solution to one of the fundamental questions about the dodecahedron altogether changed the view of the object that has been before our eyes for thousands of years.
Finding the shortest path back and forth (from one point back to the same point around the cube) for a given geometric body may seem like a simple task. After all, you will definitely return to where you started, right?
In fact, it depends on the shape or body you are walking on. If this is a sphere, then yes. (And yes, we are omitting the fact that the Earth is not an ideal sphere, and its surface is not entirely smooth.) On the sphere, paths repeat along a straight line "large circles", geodesics, for example, the equator. If you go around the equator, after about 25,000 miles you will complete a full circle and return to where you started.
In a cubic world, geodesic lines are not so obvious. Finding a straight path on one face is easy because each face is flat. But if you were walking around the cubic world around, how would you keep walking straight when you reached the edge?
There is an old funny math problem that illustrates the answer to our question. Imagine an ant in one corner of a cube that wants to get to the opposite corner. What is the shortest path on the surface of a cube from point A to point B?
Imagine the many different paths an ant might take.

But which one is the shortest? There is an ingenious way to solve the problem. Let's flatten the cube!
If the cube was made of paper, you could cut it along the edges and flatten the sheet to get this unfolded pattern.

In such a flat world, it's easy to find the shortest path from A to B: just draw a straight line between them.

To see what the geodesic line will be in the cube world, just put the cube back. Here's our shortcut.

“Aligning” the cube works because every face of the cube is flat, so nothing gets distorted when we unfold the body along the edges. (This attempt to "unfold" the sphere will not work, since we cannot flatten the sphere without distorting it.)
Now that we have an idea of what straight paths look like on a cube, let's get back to the question of whether we can follow any straight path and eventually return to where we started. Unlike a sphere, on a cube, not every straight path takes us back to the start.
But such round trip routes are possible. With one trick! Please note that the ant can continue the path we indicated above and return to where it started. On a cube, a full circle creates a path that looks more like a diamond.

Following this path (back and forth), the ant must pass through another vertex (point B) before returning to its starting point. This is the catch: every straight path that starts and ends at the same vertex must go through another vertex of the cube.
It turns out this is true for four of the five Platonic solids. In a cube, tetrahedron, octahedron, and icosahedron, any straight path that starts and ends at the same vertex must pass through some other vertex along the path. Mathematicians proved this five years ago, but the dodecahedron was not on their list. We'll come back to this a bit later.

To understand why this fact about geodesics is true for four of the five Platonic solids, we will use the tumbling method and switch to the tetrahedral world, where this method can be better demonstrated.
Imagine that you start at the top of a tetrahedron and walk in a straight line along the edge. Place the tetrahedron so that the path starts from the bottom edge.
When we encounter an edge, we flip the tetrahedron so that our path continues along the face that turns out to be below:

Such rotations make it possible to track our path in the same way as we would do on unfolding a cube:

The trajectory of rotations above represents this path on the surface of the tetrahedron:

The five turns of the tetrahedron correspond to the additional five faces intersected by our route.
Now we can imagine any path on the surface of the tetrahedron as a path in this "rotating" space. Let's define our starting point A and see where it ends up after a few turns.
When our path leaves point A, the tetrahedron falls to the opposite side. This raises point A off the ground.

Vertex A rises temporarily in our rotating world. We usually do not specify the location of point A when creating our rotating space, but here is where it might appear if we were looking down.

As our path continues, the tetrahedron falls again. He can do it in one of two possible directions, but in any case, A is again at the bottom.
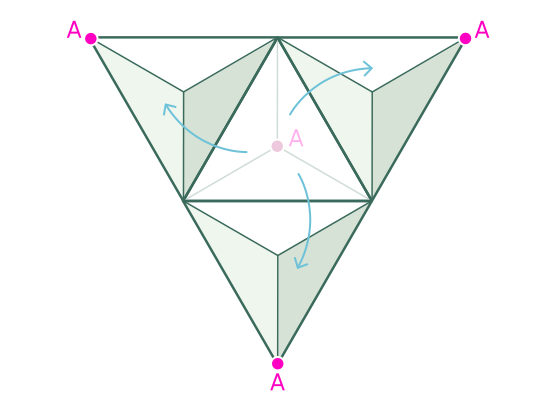
When we force the tetrahedron to fall in all possible directions, we get a somersault, which looks like this:

It turns out a kind of lattice due to the fact that the equilateral triangular faces of the tetrahedron coincide with each other.

This triangle grid tells us two interesting things about our spinning world. First, all the points at which the vertices of the tetrahedron can land are "lattice points" (shown in the diagram) or points with integer coordinates. This is because one unit in our coordinate system is equal to the length of one edge of the tetrahedron.
Second, look at where A might end up. The
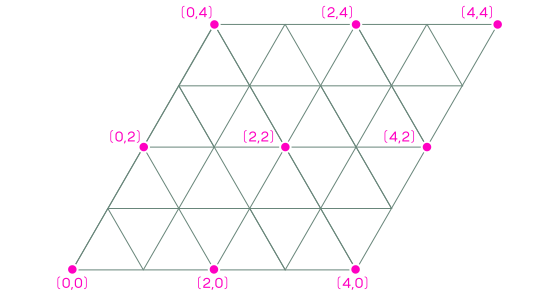
coordinates of A are always even. Whenever A is down, it comes back there after two rotations, so all possible landing spots for A are placed at intervals of two rib lengths in each direction of rotation.
Now let's see what this says about geodetic lines. Recall that a path in a tetrahedron that starts and ends at point A will be a straight line segment in rotating space, starting at point A (0,0) and ending at another point A. And when the start and end points of the path coincide at single A, what will be in the middle of the path?
Even in our confused coordinate system, the standard formula for calculating the midpoint of a line segment still works, so we can find its coordinates based on the coordinates of the endpoints.
Since both coordinates of the start point are 0 and both coordinates of the end point are even, the coordinates of the middle are integers. That is, the middle will be one of the points of the lattice, and, as we noted above, this means that it corresponds to the vertex of the triangle in rotating space.
For example, the path from (0,0) to (4,2) has a midpoint (2,1), this is the marked lattice point in our grid.

It turns out that on the surface of the tetrahedron, the path from A and back must pass through another vertex.
Since every possible “landing” for A has even coordinates, the midpoint of every geodetic path starting and ending at A will correspond to a grid point. This proves that every geodesic line from A to A on the surface of the tetrahedron must pass through another vertex.
This simple reasoning was elaborated in 2015 by mathematicians Diana Davis, Victor Dods, Cynthia Traub, and Jed Young.
They used a similar but much more complex method to prove the same for a cube. The following year Dmitry Fuks confirmedresults for octahedron and icosahedron. Because of this, we know that for a tetrahedron, cube, octahedron and icosahedron there are no straight paths going from a vertex back to itself that would not pass through another vertex.
But the question of the existence of such paths on the surface of the dodecahedron remained open until 2019, when mathematicians Jayadev Atreya, David Avlikino, and Patrick Hooper proved that it was indeed possible. In fact, they found infinitely many straight paths on the surface of the dodecahedron that begin and end at the same vertex without going through others.
Here is one of them, depicted on a scan of a dodecahedron, hiding in plain sight.

For thousands of years, Platonic solids have been studied together because they have so much in common. But now we know something new about the dodecahedron, and this clearly distinguishes it from other bodies.
This mysterious discovery shows that no matter how well we understand mathematical objects, there is always something to learn. It is important to remember that the path from problem to solution will not always be straightforward!
Tasks
1. If the length of an edge of a cube is 1, what is the shortest path for an ant from one vertex to the opposite?
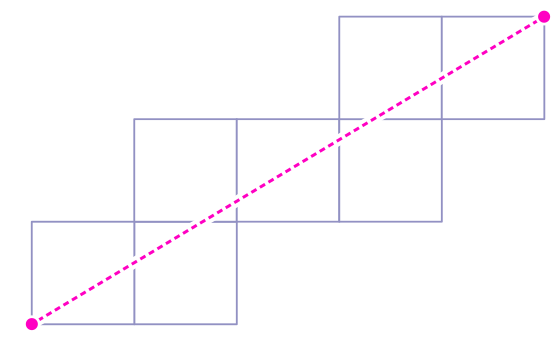
2. Explain why the diagram below cannot be a rotation path on a cube.

3. One of the difficulties in "rotating" a cube is that point A does not have a unique end position associated with the end position of the cube. For example, even if the cube is in the same place, rotating along a red or blue path, point A is in different positions. Determine where A will be after the turns along the red and blue trajectory.

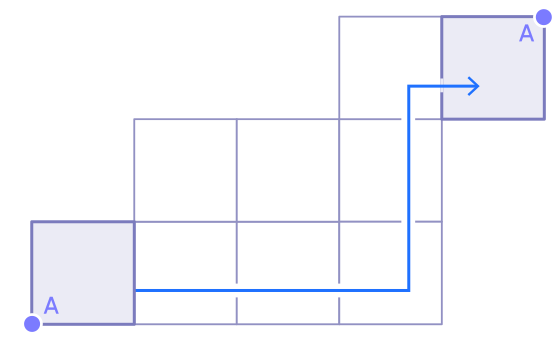
4. This is the trajectory of the cube rotations.
Draw a path on the surface of the cube, starting at point A.

Answers
Click to see answer 1
— 1 2.

, AB √5.

, AB √5.
Click to see answer 2
, 1 . , , .

, «» , .

, «» , .
, 3
.

, .


, .
, 4

