Demonstratively rotating arrays for beginners

An array is a structure that was at the origins of programming. But, despite the fact that arrays are given attention in every course of lessons in any programming language, a lot of important information related to the logic of interaction with this structure still escapes from beginners.

The purpose of this post is to collect some information about arrays that I once lacked. Post for beginners.

What is an Array?

An array is a structure of the same type of data located in memory in one non-breaking block.

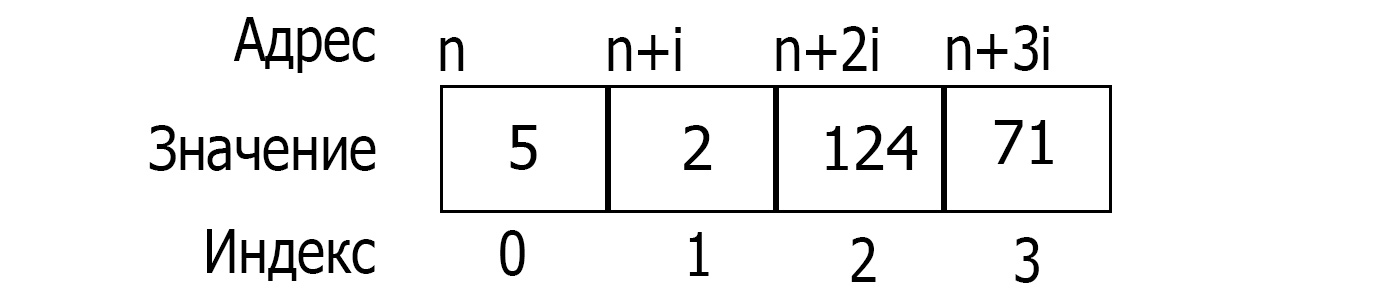
Multidimensional arrays are stored in the same way.

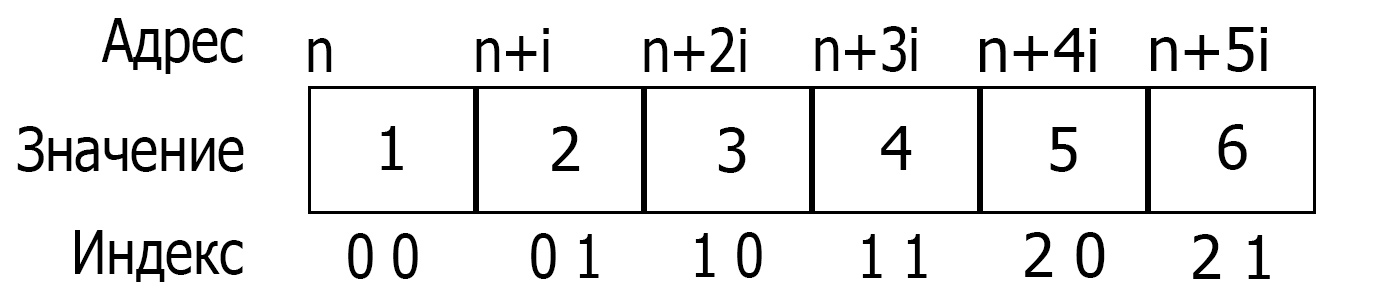
Knowing this allows us to access array elements differently. For example, we have a 2-dimensional array of 9 3x3 elements. So there are at least two ways to display it correctly:

1st option (Easiest):

int arr[3][3] {1, 2, 3, 4, 5, 6, 7, 8, 9};
int y = 3, x = 3;
for (int i = 0; i < y, ++i) {
	for (int j = 0; j < x; ++j) {
  	std::cout << arr[i][j];
  }
  std::cout << std::endl;
}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

2nd option (More difficult):

int arr [9] {1,2,3,4,5,6,7,8,9};
int x = 3, y = 3;
for (int i = 0; i < y; ++i) {
  for (int j = 0; j < x; ++j) {
		std::cout << arr[x * i + j]; // x -  
    }
  std::cout << std::endl;
}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

The formula for accessing an element of a 2-dimensional array, where width is the width of the array, col is the column we need, and row is the line we need:

Knowing the second option, it is not necessary to use it constantly, but it is still worth knowing. For example, it can be useful when you need to get rid of extra asterisks from pointers to pointers to pointers.

And this is how you can work with a three-dimensional array

int arr[8] {1,2,3,4,5,6,7,8};
int x = 2, y = 2, z = 2;
for (int i = 0; i < x; ++i) {
	for (int j = 0; j < y; ++j) {
  	for (int k = 0; k < z; ++z) {
    	std::cout << arr[x * y * i + y * j + k];
    }
    std::cout << std::endl;
  }
  std::cout << std::endl;
} 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, .

, height - , width - , depth - ( ), col - , row - :

.

, .

- , .

. , :

1) .

, .

int data[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};
int newArray[3][4];
int height = 3, width = 4;
for (int i = 0; i < height; ++i) {
	for (int j = 0; j < width; ++j) {
  	newArray[i][j] = data[i][width - j - 1];
  }
}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

.

int data[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};
int newArray[3][4];
int height = 3, width = 4;
for (int i = 0; i < height; ++i) {
	for (int j = 0; j < width; ++j) {
  	newArray[i][j] = data[height - i - 1][j];
  }
}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

2) 90 .

, , .

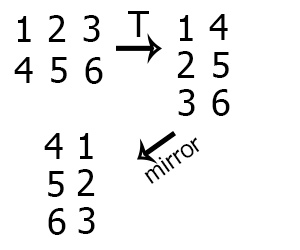
, c .

int data[3][2] = {1,2,3,4,5,6};							
int newArray[2][3];					
int height = 3, width = 2; 	//   ()
int newHeight = width, newWidth = height;

//  
for (int i = 0; i < newHeight; ++i) {
	for (int j = 0; j < newWidth; ++j) {
  	newArray[i][j] = data[j][i];			// data -  
  }
}

//     
for (int i = 0; i < newHeight; ++i) {
	for (int j = 0; j < newWidth/2; ++j) {
  	int temp = newArray[i][j];
    newArray[i][j] = newArray[i][newWidth - j - 1];
    newArray[i][newWidth - j - 1] = temp;
  }
}

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, . , .

: . new.

, IT.

, , . , , , — , . .

, , .