
The gameplay of the vehicle simulator is to control the movement of an object in space with a number of degrees of freedom. The player's actions change the vector of the instantaneous state of the system in the desired or not quite desired direction. The game is unlikely to be interesting if the object is poorly adapted to the player's control.
The adaptability of a technical system to human control ( controllability ) is a rather complex and multifaceted characteristic. The mathematical model of the behavior of a controlled object is dealt with by the theory of automatic control (TAU). The models adopted in TAU can also describe the behavior of the player - “human-operator” and “human-machine” systems.
It should be noted that the created human models are always relevant for a limited range of conditions. For this reason, solving practical problems in the field of controllability often goes beyond the scope of TAU.
Controllability of a machine refers to its ergonomic properties, which lose their meaning in isolation from the context of human activity. Under the cut, an approach to setting up a simulator model is presented, based on an experimental study of the game process.
For simulators claiming to accurately simulate existing systems, similarity to the prototype is important, no matter how poor its handling is. Optimization of the same characteristics is relevant for games that do not have a given model, for example, simulators of fantastic objects.
Leaving aside the problem of simulating a real object with a given set of characteristics, we note that the simulator will certainly not lose from the presence of a subjectively determined physicality. In other words, even an object that does not exist in nature may or may not correspond to the player's expectations regarding his (object) behavior. The factor of natural behavior of the object must be taken into account.
Formulation of the problem
For the simulator, it is necessary to adjust the coefficients of the mathematical model of the vehicle so as to ensure its best handling. Optimization should be performed based on experimental data. It is desirable to get a model that looks natural to the player.
System Description
In our experiments we will use a simulator with 3D graphics.
The complexity of the mathematical model of a real vehicle is limited only by the accepted level of abstraction and the roughness of the assumptions used. The complexity of the model in the problem being solved here is determined by the rational level of the naturalness of the game.
The following simplifications will be applied below:
1. The direction of movement of the object is taken to coincide with its longitudinal axis.
2. The rotational motion of an object can be considered as the sum of independent components - rotational motions relative to the three axes of the coordinate system (CCS) associated with the object.
3. Angular acceleration in a separate control channel (around a separate CCS axis) is determined by a linear combination of the current values of the control action and the angular velocity in this channel.
The acceptability of the first simplification in modeling real objects is determined by the properties of the system and the problem being solved. For example, a well-known property of darts is their ability to fly after being thrown "with a point forward." This simple model is enough to draw a useful conclusion: Don't throw the dart up over you.

But if an accurate model is needed to determine the consequences of contact of a dart with a target, then it should be borne in mind that in flight its velocity vector makes a certain angle with the longitudinal axis.
The constancy of the direction of the velocity vector in the object's coordinate system corresponds to the biomechanics of walking: it is easiest for a person to walk, maintaining the state of "facing forward". Movement in unusual directions, on the contrary, impairs the player's vision and requires additional mental effort from him.
Item 2 establishes the mutual isolation of control channels "attached" to the axes of the SSC.
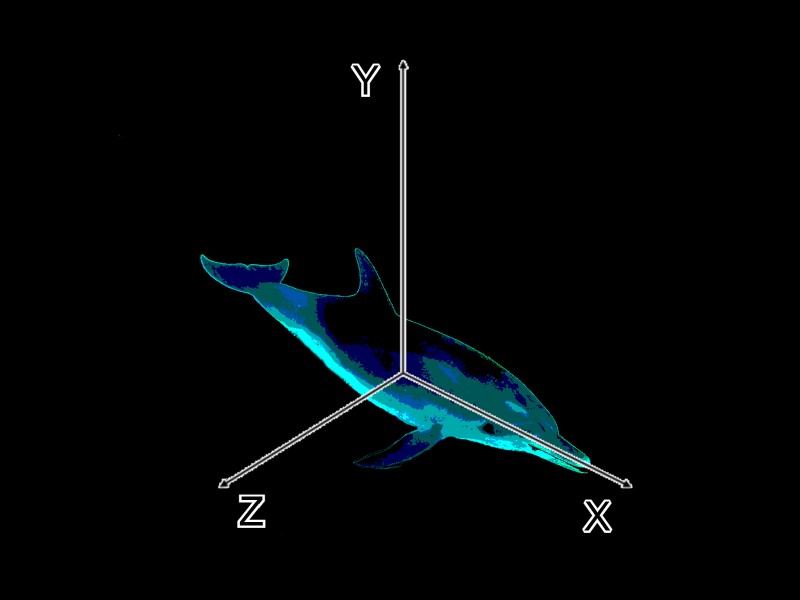
SSC axes: longitudinal ( X ) is directed from the tail to the nose of the object, vertical ( Y ) is directed upward in the plane of symmetry of the object at its initial position, lateral ( Z ) is directed perpendicular to the first two to the right. Accordingly, rotation around the X axis - lateral channel, around the Y - axis - track channel, around the Z - axis - longitudinal channel.
In accordance with clause 2 of the adopted simplifications, there are no cross-links between the control channels of the object. Real systems always correspond to such a model with some error caused, for example, by the presence of gyroscopic moments. The lack of cross-links is an advantage from the player's point of view.
Item 3 establishes the presence of only two torques in each control channel:
- control torque proportional to the signal from the player's control;
- damping moment proportional to the current angular velocity.
The differential equation of rotation around the i- axis is as follows:

Here omega is the angular velocity of rotation, t is the time, x is the control signal, and the coefficients on the right side of the equation are the partial derivatives of the angular acceleration from the control signal and the angular velocity.
The first coefficient will be called the control efficiency coefficient , the second - the damping coefficient .
The angular acceleration is measured in [rad / s 2], the angular velocity is in [rad / s]. The control signal is usually measured in units of movement of the levers or efforts on them, less often in units of the position of the intermediate elements of the control system, but for control from the keyboard we will take this value as dimensionless. The dimension of the damping factor is [1 / s], and the control efficiency factor is [rad / s 2 ], taking into account the adopted dimension of the control signal.
Required theoretical information
, (1), . , . , :
(1) – x, – . :

(t) – , y(t) – , y – , k – , T – , .
(1) (2) :
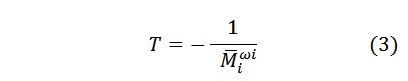
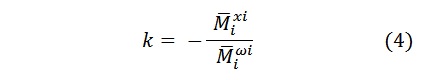
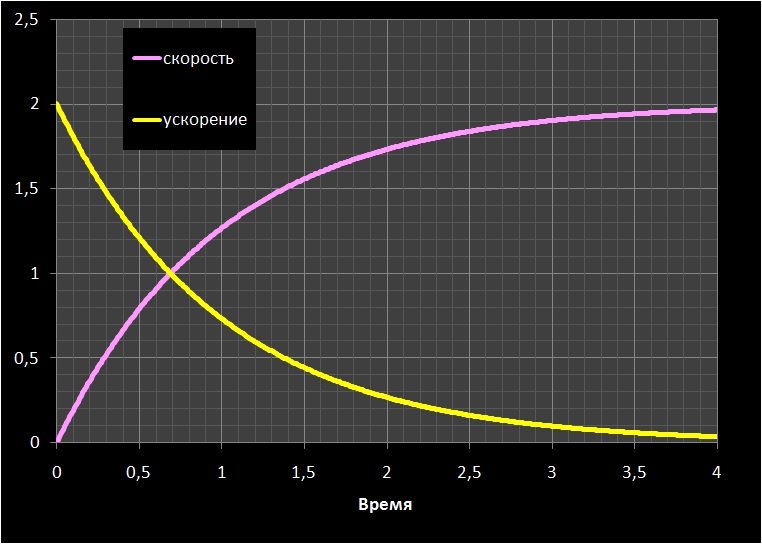
( ) , . () – . – .
:

:
:
1. ( ), , .
2. , , .
3. , , , k.
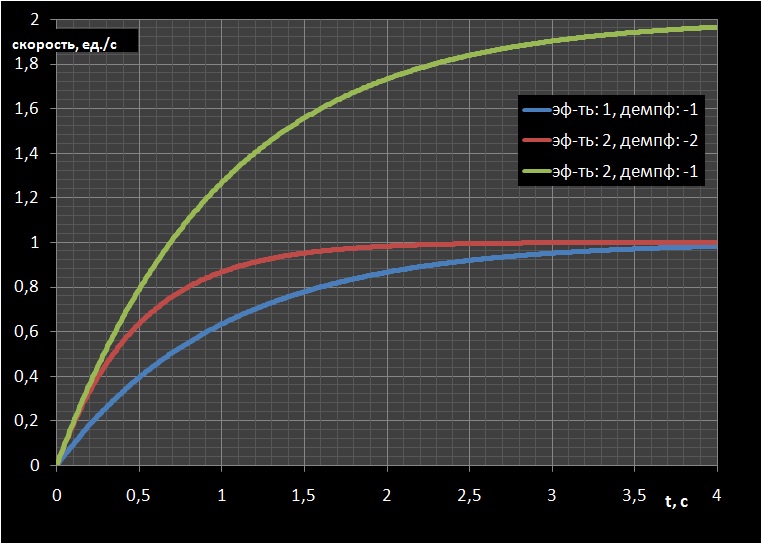
, . k T.
. .
. , : — , — , – . — - , .
, - , . .
, , . .

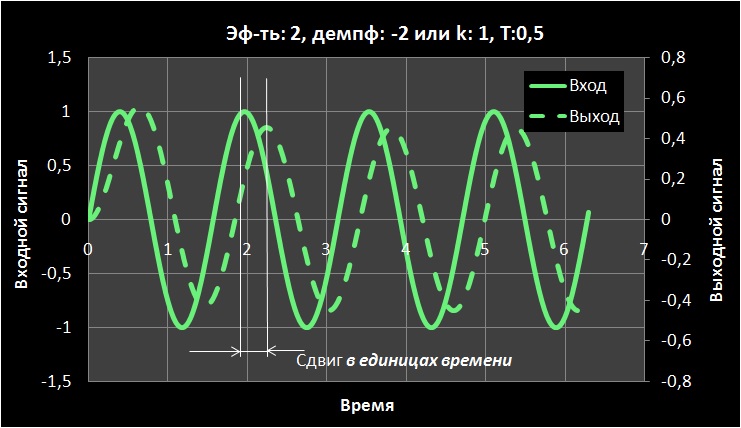
, . .
( ) k. .
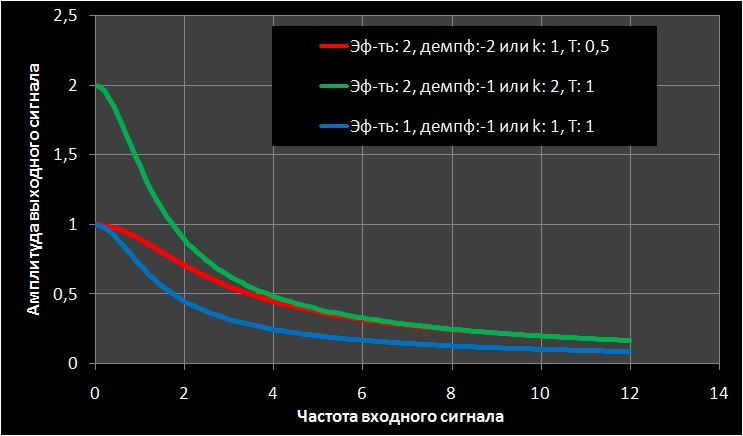
T ( ). T .
( T).
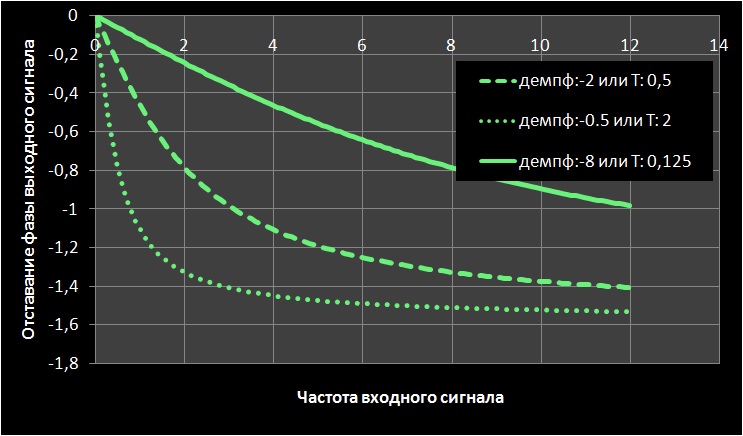
, /2. T.
: ( T) .
- ;
- ();
- ().
(1) – x, – . :

(t) – , y(t) – , y – , k – , T – , .
(1) (2) :
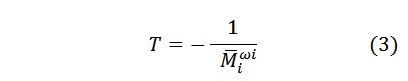
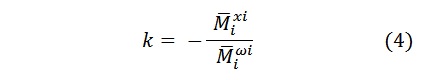
( ) , . () – . – .

:

:
- k ;
- T « », , t = 3T 0,95k.
:
1. ( ), , .
2. , , .
3. , , , k.

, . k T.
. .
. , : — , — , – . — - , .
, - , . .
, , . .


, . .
( ) k. .

T ( ). T .
( T).

, /2. T.
: ( T) .
Experimental conditions and model quality criteria
Better controllability of the object should provide a more efficient solution to the problem by the player. But different tasks require different controllability: exact adherence to the parameters of a given mode of movement differs significantly from intensive maneuvering.
Finding a universal model for any task is inevitably associated with a compromise. The experimental conditions determine the subjective balance shift in favor of certain tasks. However, the specific conditions of the game must be chosen.
For the study, we will use the problem of a controlled object visiting the maximum number of locations out of the specified ones in a limited time. An effective solution to this problem requires intensive maneuvering.
The vehicle will be controlled with restrictions on the roll and pitch angles ( 60 degrees in both directions for both angles): going beyond the limits will lead to an accident. Also, a collision with a horizontal surface located above the object leads to an accident. This part of the conditions is responsible for the component of maintaining the parameters in the player's task.
The value of the linear velocity module of the object is assumed constant. This means that the accelerator control, as well as the unevenness of the medium resistance, is absent in the simulator.
Player efficiency indicator - the number of locations visited before the end of time ( 60seconds) or before the accident. The more locations visited, the better the model is considered. Each model (set of coefficient values) provides three passes of the game with the median score taken into account.
When planning experiments, it is important to minimize the influence of the learning factor. For this, the order of experiments was determined, in which each model is launched in the first, second and third thirds of the study:
A, B, C ... N, O,
A, B, C ... N, O,
A, B, C ... N, O ...
Each experimental playthrough was preceded by one practice game with the corresponding model.
Simulator
You can experiment with the model coefficients yourself here .
Odds management is in the upper right corner of the screen. The "efficiency" parameter is the control efficiency coefficient, the "damping" parameter is the damping coefficient taken with the opposite sign.
Game control:
- Space - start of the game;
- W / S - rotation around the SSC Z axis , nose down / nose up;
- A / D - rotation around the Y- axis of the SSK, turn left / turn right;
- 4/6 on the numpad - rotation around the X- axis of the SSK, roll left / roll right.
The indicator windshield player sees the artificial horizon , and the current heading value ( «heading» ) and depth ( «depth» ), i.e. the distance to dangerous surface. It also shows the rest of the game time and the current result ( "score" ) - the number of visited locations.
The simulator code is written in JavaScript using the Three.js library . The values of the parameters of the object's motion are updated in the game loop by numerically integrating equation (1) using the Euler method. In each iteration, the update () method of the object is called vehicle that performs calculations for each control channel:
vehicle.update = function () {
// :
game.elapsed = (new Date() - game.time) / 1000;
game.time = new Date();
// ...
// :
vehicle.omegaX += (vehicle.epsilonX - vehicle.omegaX * vehicle.damping) * game.elapsed;
vehicle.omegaY += (vehicle.epsilonY - vehicle.omegaY * vehicle.damping) * game.elapsed;
vehicle.omegaZ += (vehicle.epsilonZ - vehicle.omegaZ * vehicle.damping) * game.elapsed;
// ...
}
The epsilonX , epsilonY, and epsilonZ fields of the vehicle object contain the angular acceleration components in the absence of damping. The value of each of these fields is obtained by “multiplying” the input signal by the control efficiency factor:
function init() {
// ...
// :
document.addEventListener('keydown', function (event) {
if (game.state == "READINESS")
if (event.code == "Space") {
// ...
}
if (game.state == "RUN")
switch (event.code) {
case "KeyW":
vehicle.epsilonZ = vehicle.efficiency;
break;
case "KeyS":
vehicle.epsilonZ = -vehicle.efficiency;
break;
case "KeyA":
vehicle.epsilonY = -vehicle.efficiency;
break;
case "KeyD":
vehicle.epsilonY = vehicle.efficiency;
break;
case "Numpad4":
vehicle.epsilonX = vehicle.efficiency;
break;
case "Numpad6":
vehicle.epsilonX = -vehicle.efficiency;
break;
}
});
document.addEventListener('keyup', function (event) {
switch (event.code) {
case "KeyW":
vehicle.epsilonZ = 0;
break;
case "KeyS":
vehicle.epsilonZ = 0;
break;
case "KeyA":
vehicle.epsilonY = 0;
break;
case "KeyD":
vehicle.epsilonY = 0;
break;
case "Numpad4":
vehicle.epsilonX = 0;
break;
case "Numpad6":
vehicle.epsilonX = 0;
break;
}
});
// ...
}
Experiment Results
The quality indicator of the model will be considered as a function of two variables. Accordingly, the results of the study graphically represent a 3D surface, each point of which defines its own model of the controlled object.

Let's consider the key features of some models. On the chart, the discussed models are indicated in Latin letters.
With the minimum value of the control efficiency coefficient ( 0.5 rad / s 2 ), there is a model with the best value of the damping coefficient (point A ). Model A is characterized by a weak ability of the object for dynamic maneuvers.
Changing model A towards increased damping leads to the creation of models with extremely low maximum angular velocity values. The object finally loses its ability to maneuver.
Changing model A in the direction of decreasing damping partially improves the object's maneuverability, but the overall quality of the system decreases due to the deterioration of its dynamic properties: a swinging problem arises, control requires constant compensating actions from the player.
In the absence of damping, there is a model with optimal control efficiency ( B ). Its management efficiency is higher than that of model A, which provides good maneuverability. In this case, the buildup problem is exacerbated compared to model A , completely devoid of damping.
Changing model B towards more efficient control brings the swing problem to a level where the player's full attention is given to fighting it. Further, maneuvering without going beyond the restrictions becomes impossible.
Model C combines the advantages of the models A and Bed and . The object is managed efficiently enough, but without swinging. The value of the game performance indicator for model Csignificantly higher than previous models. However, this model is not the most effective one.
Form isolines performance game around point C shows that the improvement in the result corresponds to the motion direction model D .
This movement corresponds to a decrease in the value of T while maintaining k at a constant level (about 0.6 rad / s). Models between C and D outperform Con the effectiveness of the game. When playing with these models, the control object follows the keystrokes more closely.
When moving from model C to model D , another change occurs: the deterioration of the natural behavior of the object. The time constant approaches the level at which the duration of the transient and the phase shift of the output signal are no longer noticeable to the user.
Changing the model D towards a further decrease in the value of T while maintaining the value of k no longer gives significant improvements, because the phase shift of the output signal and the duration of the transient process in the model D is already small enough for the player to perceive.
The models obtained by further “improvement” of D , from the player's point of view, do not differ from the implementation of the amplifying link: there is no angular acceleration of the object in the game, the angular velocity instantly takes on a steady value when the key is pressed.
The analysis made it possible to draw the following conclusions :
1. The optimal values of the model parameters correspond to its degeneration into an amplifying link (the value of k is about 0.6 rad / s, T = 0 s) and the loss of the natural behavior of the object.
2. The model that provides good controllability with the natural behavior of the object corresponds to point C on the graph (control efficiency coefficient: from 2 to 3 rad / s 2 ; damping coefficient: from -4.5 to -3.5 1 / s).
3. Changing the model C in the direction of decreasing the value of T at k = const makes it possible to obtain an object with improved controllability due to the deterioration of the naturalness of its behavior.
Unaccounted for factors
Along with the simplifications of the physics of the controlled object, the quality of the research results is influenced by other simplifications of the research conditions:
1. The controllability model was described by two values of the parameters; the object behaved the same in all control channels. To obtain an accurate picture, the values of six parameters should be varied, since there is no reason to consider the player's properties the same for all channels.
2. The results obtained are relevant for the settings of the camera's field of view used in the game. Changing this parameter will have a noticeable effect on the interaction of the player with the object.
The most serious flaw in the study is the lack of statistics. Any ergonomic research should focus on the properties of the target audience as a whole. More complete results can be obtained with the participation of a group of players.