
The data flow in this table is a bit tricky to follow, so here is an equivalent chart that represents the table as a graph:

Round the El Farolito super vegi burrito cost to $ 8, so on delivery worth $ 2, the total amount will be $ 20.
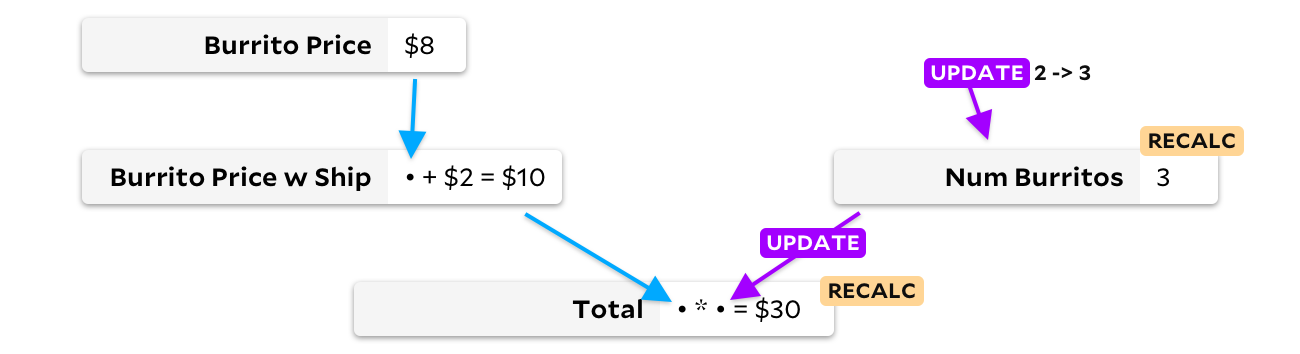
Oh, I completely forgot! One of my friends is not enough for one burrito, he needs two. So I really want to order three. If updated
Num Burritos
, the naive spreadsheet engine can recalculate the entire document by recalculating the cells with no input first and then recalculating each cell with the ready input until the cells run out. In this case, we will first calculate the burrito price and quantity, then the shipping burrito price, and then a new $ 30 total.

This simple strategy of recalculating an entire document may seem wasteful, but it's actually better than VisiCalc, the first spreadsheet ever and the first killer app that made Apple II computers popular. VisiCalc recalculated cells from left to right and top to bottom many times, scanning them over and over again, although none of them changed. Despite this "interesting" algorithm, VisiCalc remained the dominant spreadsheet software for four years. His reign ended in 1983, when Lotus 1-2-3 took over the natural-order recalculation market. This is how Tracy Robnett Licklider described him in Byte magazine :
Lotus 1-2-3 used natural ordering, although it also supported VisiCalc row and columnar modes. Natural recalculation maintained a list of cell dependencies and recalculated cells based on dependencies.
Lotus 1-2-3 implemented the recalculate all strategy shown above. During the first decade of spreadsheet development, this was the most optimal approach. Yes, we recalculate every cell in the document, but only once.
But what about the price of a delivery burrito
Really. In my example of three burritos, there is no reason to recalculate the price of one burrito with delivery, because changing the quantity of burritos in the order cannot affect the price of the burrito. In 1989, one of Lotus's competitors figured this out and created SuperCalc5, presumably naming it after the super burrito theory behind the algorithm. SuperCalc5 recalculated "only cells that depend on the changed cells", so the update of the burrito count was something like this:
By updating the cell only when the input data changes, we can avoid recalculating the price of the burrito with delivery. In this case, we will save only one addition, but in large spreadsheets the savings can be much more significant! Unfortunately, we have a different problem now. Let's say my friends now want meat burritos, which are a dollar more expensive, and El Farolito adds $ 2 to their order regardless of the number of burritos. Before we recalculate something, let's look at the graph:
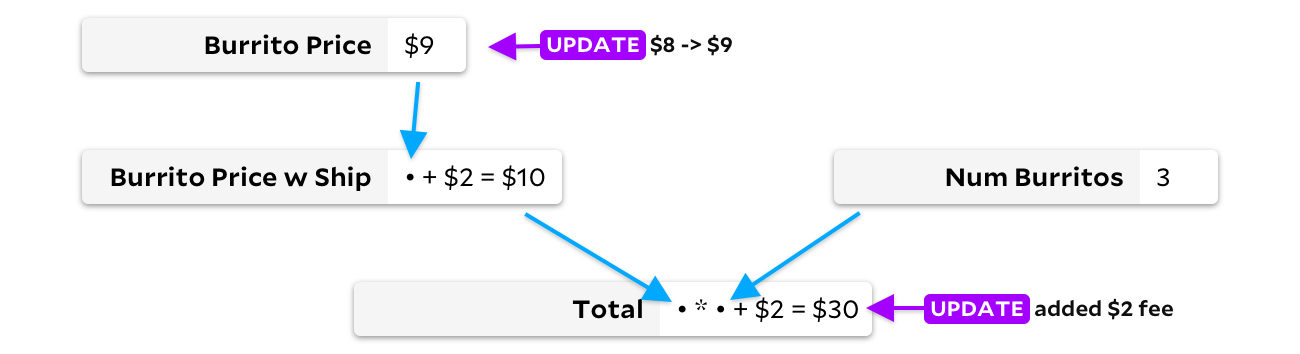
Since there are two cells updating here, we have a problem. Should you recalculate the price of one burrito first or the total? Ideally, we first calculate the burrito price, notice the change, then recalculate the delivery burrito price, and finally recalculate the Total. However, if we recalculate the total first, instead, we would have to recalculate it a second time once the new $ 9 burrito price spreads down the cells. If we don't compute cells in the correct order, this algorithm is no better than recalculating the entire document. As slow as VisiCalc in some cases!
Obviously, it is important for us to determine the correct order of updating the cells. In general, there are two solutions to this problem: dirty marking and topological sorting.
The first solution involves labeling all cells downstream of the updated cell. They are marked as dirty. For example, when we update the price of a burrito, we mark the downstream cells
Burrito Price w Ship
and
Total
, before doing any recalculation:
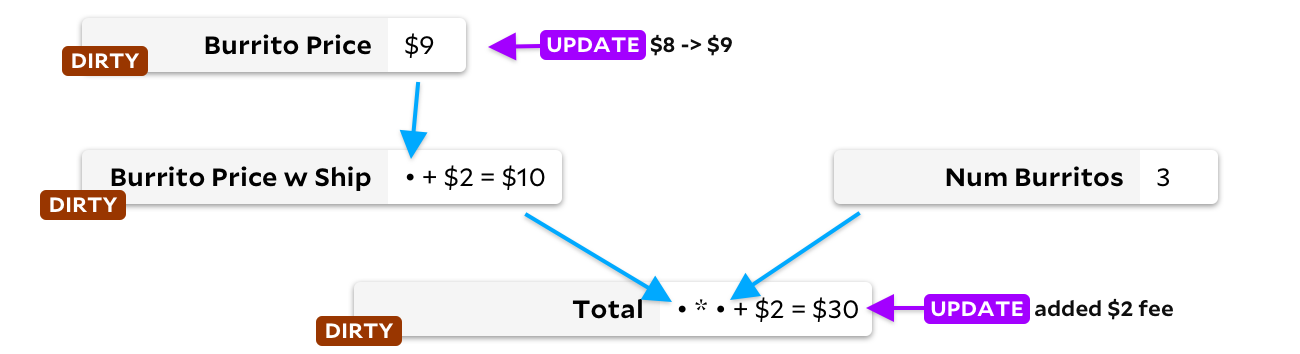
Then, in a loop, we find a dirty cell with no dirty inputs - and recalculate it. When there are no dirty cells left, we're done! This solves our dependency problem. However, there is one drawback - if the cell is recalculated and we find that the new result is the same as the previous one, we will recalculate the subordinate cells anyway! A little extra logic will help avoid the problem, but unfortunately we still spend time marking cells and removing markings.
The second solution is topological sort. If a cell has no input, we mark its height as 0. If it does, we mark the height as the maximum of the input cells plus one. This ensures that each cell has a greater height value than any of the incoming cells, so we simply keep track of all cells with the changed input, always choosing the cell with the lowest height to recalculate first:
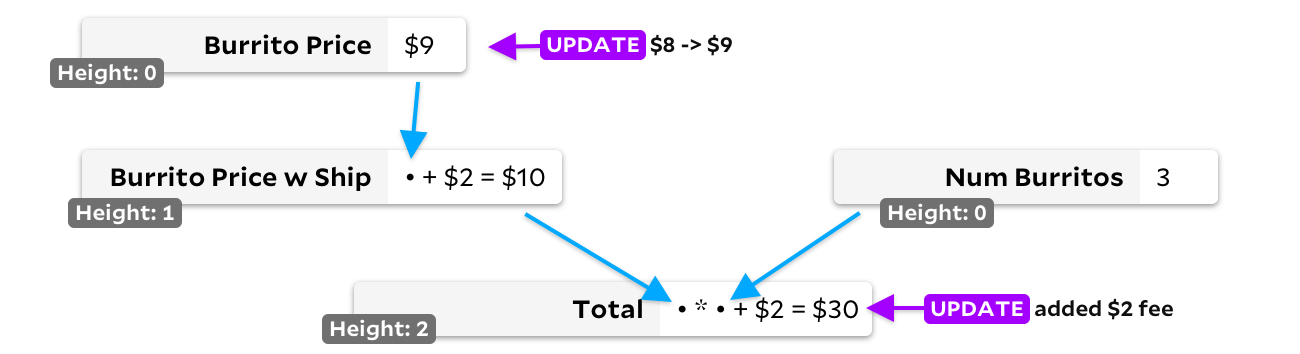
In our double update example, the price of the burrito and the total amount will initially be added to the conversion heap. The burrito price is lower and will be recalculated first. Since its result has changed, we will then add the price of the delivery burrito to the recalculation heap, and since it also has a shorter height than
Total
then it will be recalculated before we finally recount
Total
.
This is much better than the first solution: no cell is marked dirty unless one of the incoming cells really changes. However, this requires the cells to be kept in sorted order pending recalculation. When used on the heap, this results in slowdown
O(n log n)
, which is asymptotically slower in the worst case than Lotus 1-2-3 recalculated strategy.
Modern Excel uses a combination of pollution and topological sorting , see their documentation for details.
Lazy evaluation
We have now more or less achieved the recalculation algorithms in modern spreadsheets. I suspect that, in principle, there is no business justification for further improvements, unfortunately. People have already written enough Excel formulas to make migration to any other platform impossible. Fortunately, I am not business savvy, so we will consider further improvements anyway.
Aside from caching, one of the interesting aspects of a spreadsheet-style computational graph is that we can only compute the cells we are interested in. This is sometimes referred to as lazy evaluation or demand-driven computation. As a more specific example, here's a slightly expanded burrito spreadsheet graph. The example is the same as before, but we have added what is best described as “salsa calculation”. Each burrito contains 40 grams of salsa and we do a quick multiplication to find out how much salsa is in the entire order. Since we have three burritos in our order, there will be a total of 120 grams of salsa.

Of course, discerning readers have already noticed the problem: the total weight of salsa in an order is a pretty useless metric. Who cares if it's 120 grams? What should I do with this information? Unfortunately, a typical spreadsheet will spend cycles on salsa calculations, even if we don't need those calculations most of the time.
This is where lazy recalculation can help. If we somehow indicate that we are only interested in the result
Total
, we could recalculate this cell, its dependencies and not touch the salsa. Let's call it an
Total
observed cell as we are trying to look at its result. We can also call
Total
three of its dependencies necessary.cells, since they are needed to calculate some observed cell.
Salsa In Order
and
Salsa Per Burrito
call it unnecessary .
To solve this problem, some of the Rust teammates created the Salsa framework , explicitly naming it after the unnecessary salsa computation that wasted their computer cycles. Surely they can explain better than me how it works. Very roughly, the framework uses revision numbers to keep track of whether a cell needs recalculation. Any mutation in a formula or input increases the global revision number, and each cell tracks two revisions:
verified_at
for the revision whose result was updated and
changed_at
for the revision whose result was actually changed.
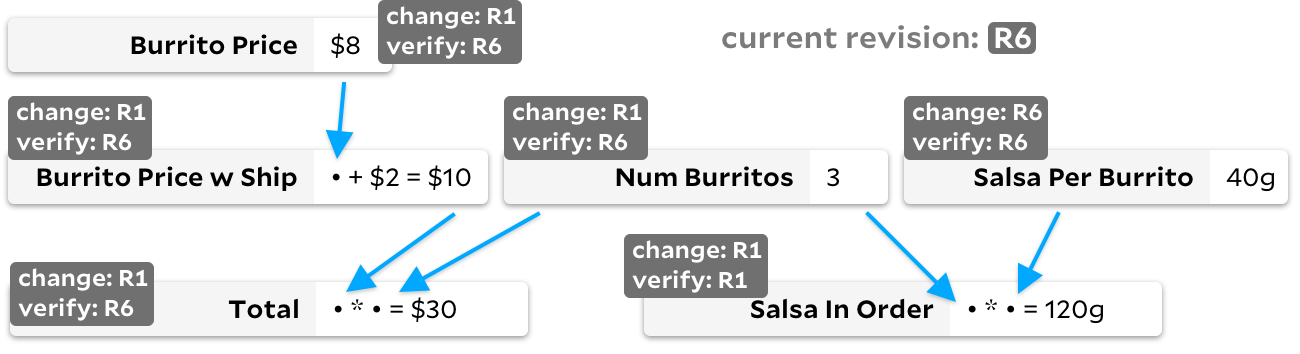
When the user indicates that he needs a new value
Total
, we first recursively recalculate all the cells needed for
Total
, skipping the cells where the revision
last_updated
is equal to the global revision. Once the dependencies are
Total
updated, we rerun the actual formula
Total
only if either Burrito Price w Ship or has a
Num Burrito
revision
changed_at
greater than the revision checked
Total
... This is great for Salsa's rust-analyzer, where simplicity is important and each cell is time consuming to compute. However, in the graph with the burrito above, you can notice the drawbacks - if it is
Salsa Per Burrito
constantly changing, then our global revision number will often increase. As a result, each observation
Total
would require traversing three cells, even if none of them changed. No formulas will be recalculated, but if the graph is large, iterating over all cell dependencies can be costly.
Faster options for lazy evaluation
Instead of inventing new lazy algorithms, let's try the two classic spreadsheet algorithms mentioned earlier: labeling and topological sorting. As you can imagine, the lazy model complicates both of these tasks, but both are still viable.
Let's look at the markings first. As before, when we change a cell's formula, we mark all downstream cells as dirty. So when updating,
Salsa Per Burrito
it will look something like this:

But instead of immediately recalculating all the dirty cells, we wait until the user observes the cell. Then we run the Salsa algorithm on it, but instead of rechecking dependencies with outdated version numbers
verified_at
, we only recheck cells that are marked dirty. Adapton uses this technique . In such a situation, observing the cell
Total
reveals that it is not dirty, and therefore we can skip the graph pass that Salsa would have performed!
If you observe it
Salsa In Order
, then it is marked as dirty, and therefore we will recheck and recalculate both and
Salsa Per Burrito
, and
Salsa In Order
. Even here, there are advantages over using only revision numbers, as we can skip recursively through a still blank cell
Num Burritos
.
Lazy dirty labeling works fantastic at frequently changing the set of cells we are trying to observe. Unfortunately, it has the same disadvantages as the previous dirty marking algorithm. If a cell with many downstream cells changes, then we spend a lot of time marking the cells and unmarking, even if the input does not actually change when we go to the recalculation. In the worst case, each change leads to the fact that we mark the entire graph as dirty, which gives us roughly the same order of performance as the Salsa algorithm.
In addition to messy labeling, we can also adapt topological sorting for lazy evaluation. This method uses the Incremental library from Jane Street, and it takes some serious tricks to get it working properly. Before implementing lazy evaluation, our topological sort algorithm used a heap to determine which cell to recalculate next. But now we want to recalculate only those cells that are needed. How? We do not want to walk the entire tree from the observed cells like Adapton, since a full walk through the tree destroys the whole purpose of the topological sort and gives us performance characteristics similar to Adapton.
Instead, Incremental maintains a set of cells that the user has marked as watched, as well as the set of cells required for any watched cell. Whenever a cell is marked as observable or unobservable, Incremental walks through the dependencies of that cell to ensure that the required labels are applied correctly. Then we add cells to the recalculation heap only if they are marked as needed. In our burrito graph, as long as it
Total
is part of an observable set, the change
Salsa in Order
will not result in any passage through the graph, since only the necessary cells are recalculated:

This solves our problem without eagerly walking through the graph to mark cells as dirty! We must still remember that the cell
Salsa per Burrito
is messy to recount later if necessary. But unlike Adapton's algorithm, we don't need to push that single dirty label down the entire graph.
Anchors, a hybrid solution
Both Adapton and Incremental traverse the graph even if they do not recalculate cells. Incremental walks up the graph when the set of observed cells changes, and Adapton walks down the graph when the formula changes. With small graphs, the high cost of these passes may not be immediately apparent. But if the graph is large and the cells are relatively cheap to compute - often this is the case with spreadsheets - you will find that most of the computation is wasted in unnecessary walking around the graph! When cells are cheap, marking a bit on a cell can cost about the same as simply recalculating a cell from scratch. Therefore, ideally, if we want our algorithm to be significantly faster than a simple computation, we should avoid unnecessary walking around the graph as much as possible.
The more I thought about this problem, the more I realized that they are wasting time traversing the graph in roughly opposite situations. In our burrito graph, let's imagine the cell formulas rarely change, but we switch quickly, observing first
Total
and then
Salsa in Order
.
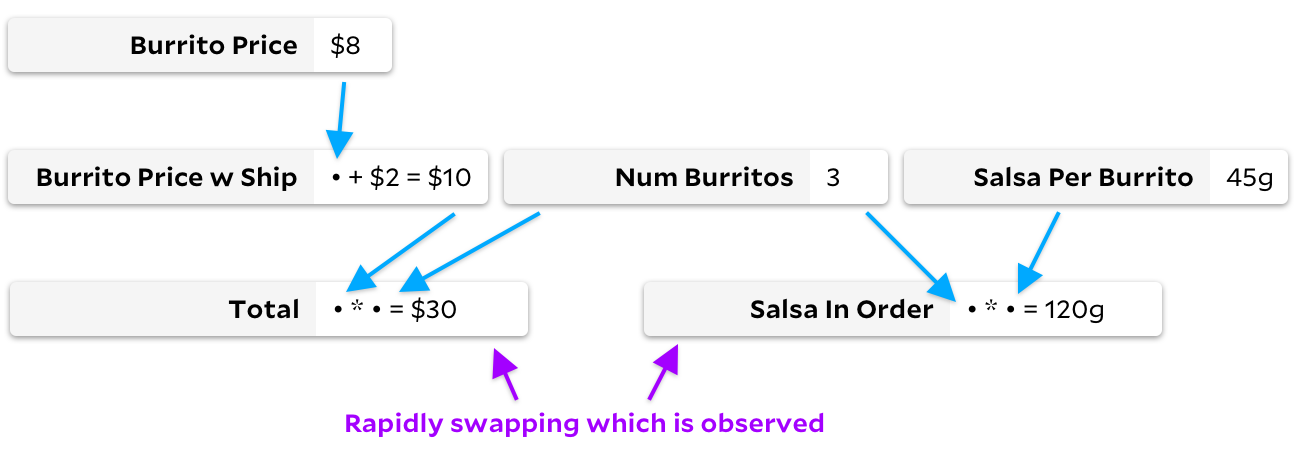
In this case, Adapton will not walk the tree. None of the input data changes and therefore we don't need to mark any cells. Since nothing is flagged, every observation is cheap because we can just immediately return the cached value from a blank cell. However, Incremental does not perform well in this example. Although no values are recalculated, Incremental will repeatedly mark and uncheck many cells as needed or unnecessary.
Otherwise, let's imagine a graph where our formulas are changing rapidly, but we are not changing the list of observed cells. For example, we might imagine ourselves watching
Total
by rapidly changing the price of a burrito from
4+4
to
2*4
.
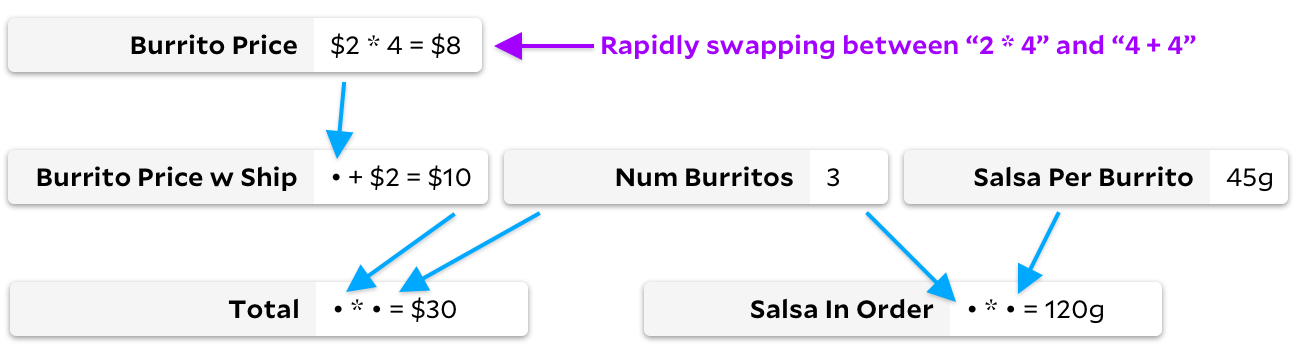
As in the previous example, we don't actually recalculate many cells:
4+4
and
2*4
equals
8
, so ideally we only recalculate this arithmetic when the user makes this change. But unlike the previous example, Incremental now avoids tree walking. With Incremental, we have cached the fact that the burrito price is a required cell, so when it changes, we can recalculate it without going through the graph. With Adapton, we waste time marking
Burrito Price w Ship
and
Total
how messy, even if the result
Burrito Price
doesn't change.
Given that each algorithm works well in the degenerate cases of the other, why not ideally just detect those degenerate cases and switch to a faster algorithm? This is what I tried to implement in my own library Anchors . It runs both algorithms simultaneously on the same graph! If it sounds crazy, unnecessary, and too complicated, it’s probably because it is.
In many cases, Anchors follow the Incremental algorithm exactly, thus avoiding the degenerate Adapton case above. But when cells are marked as unobservable, their behavior diverges slightly. Let's see what's going on. Let's start by marking it
Total
as an observed cell:
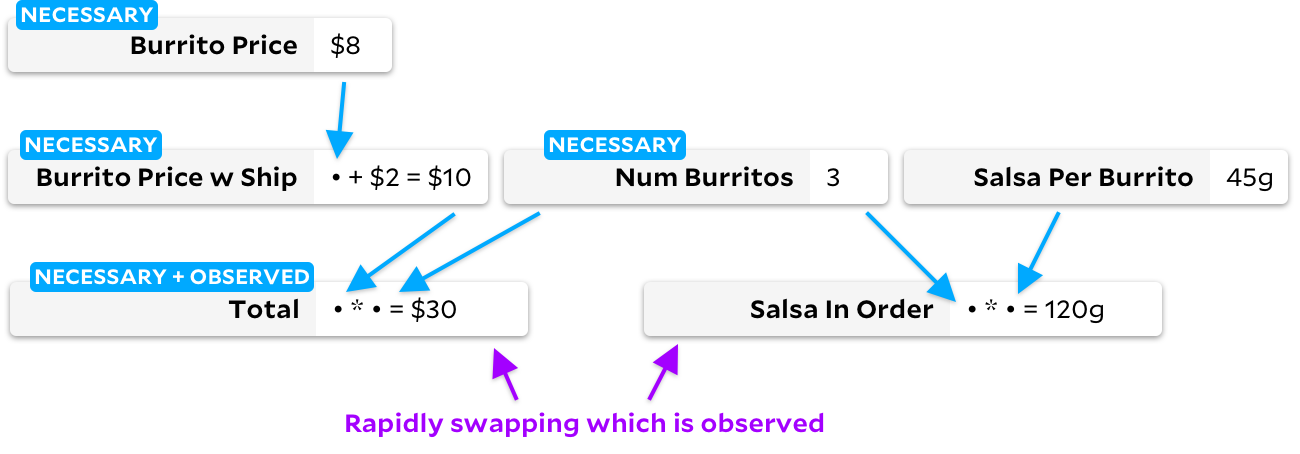
If you then mark it
Total
as an unobservable cell, and
Salsa in Order
as an observable, the traditional Incremental algorithm will change the graph, going through all the cells in the process:
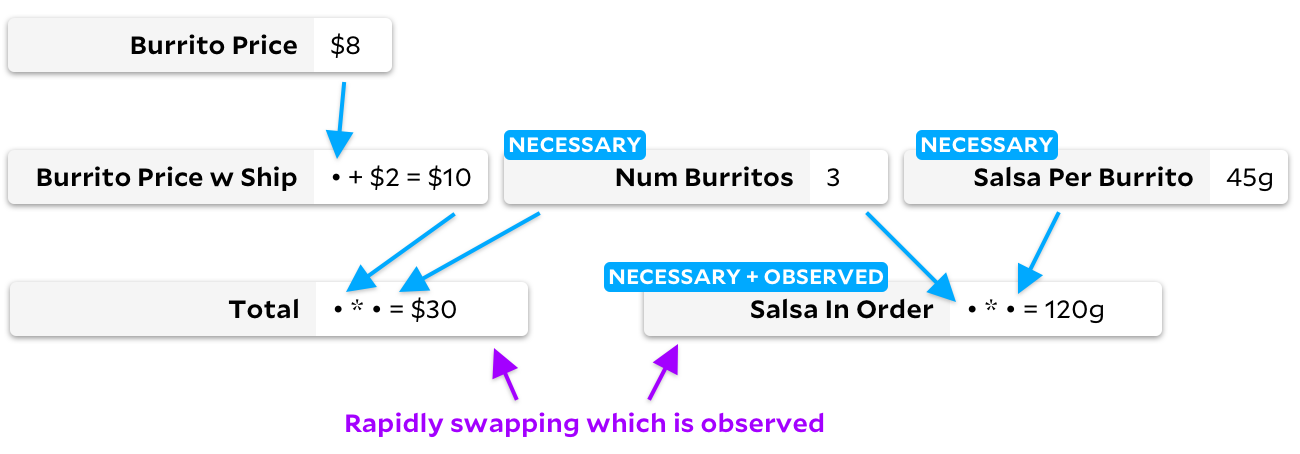
Anchors for this change also bypasses all cells, but creates another graph:
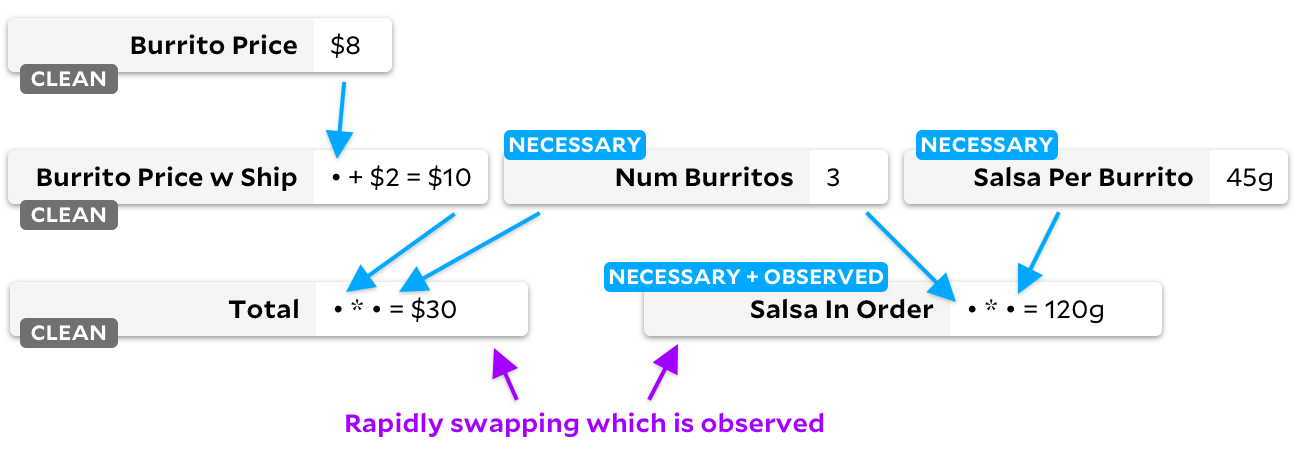
Pay attention to the flags of the "clean" cells! When a cell is no longer needed, we mark it as blank. Let's see what happens when we move from observation
Salsa in Order
to
Total
:
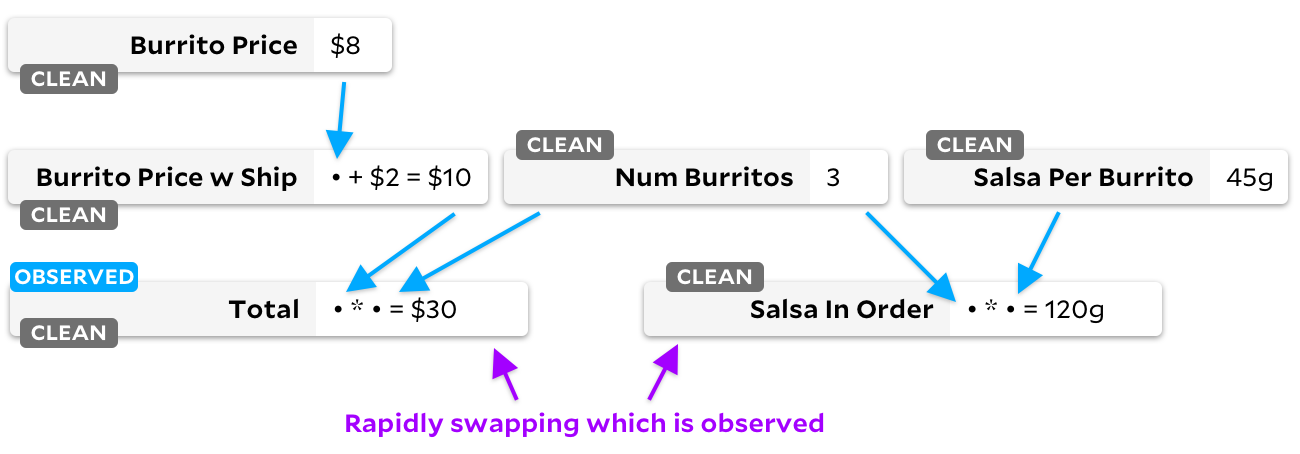
Right - our graph now has no "necessary" cells. If a cell has a "clean" flag, we never mark it as observable. From now on, no matter which cell we mark as observed or unobserved, Anchors will never waste time walking the graph - she knows that none of the inputs have changed.
Looks like El Farolito has announced a discount! Let's cut the price of the burrito by a dollar. How does Anchors know to recalculate the amount? Before any recalculation, let's see how Anchors sees the graph immediately after the burrito price changes:

If the cell has a clear flag, we run the traditional Adapton algorithm on it, willingly marking the downstream cells as dirty. When we later run the Incremental algorithm, we can quickly tell that there is an observable cell marked dirty, and we know to recalculate its dependencies. The final graph will look like this:
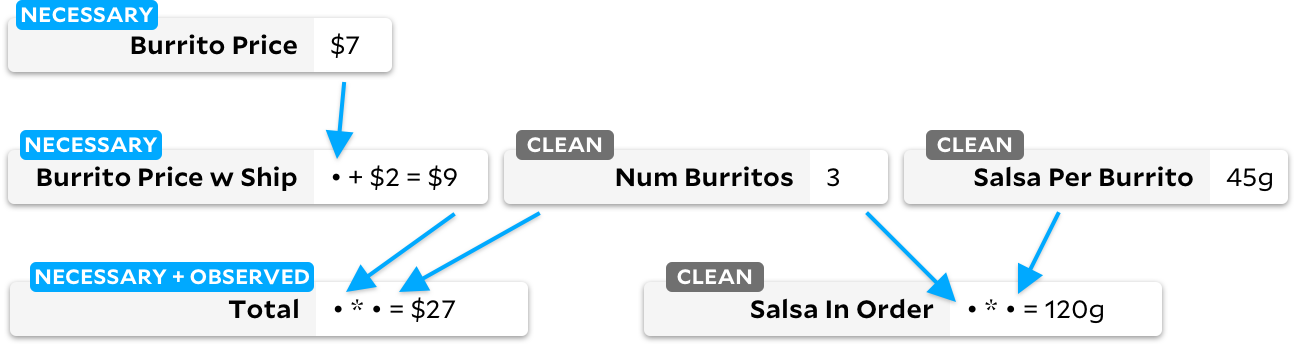
We recalculate cells only when necessary, so whenever we recalculate a dirty cell, we also mark it as needed. At a high level, you can think of these three states of cells as a cyclic state machine:

On the required cells, run the Incremental topological sorting algorithm. On the rest, we run the Adapton algorithm.
Burrito syntax
In conclusion, I would like to answer the last question: so far we have discussed a lot of problems that a lazy model causes for our table recalculation strategy. But the problems are not only in the algorithm: there are also syntactic problems. For example, let's put together a table to choose an emoji burrito for our client. We would like to write a statement
IF
in a table like this:

Since traditional spreadsheets are not lazy, we can calculate
B1
,
B2
and
B3
in any order, and then calculate the cell
IF
... However, in a lazy world, if we can calculate the value of B1 first, then we can look at the result to find out which value needs to be recalculated - B2 or B3. Unfortunately, traditional spreadsheets
IF
cannot express this!
Problem:
B2
simultaneously references a cell
B2
and retrieves its value. Most of the lazy libraries mentioned in the article instead explicitly distinguish between a cell reference and the act of retrieving its actual value. In Anchors, we refer to this cell reference as an anchor. Just like a burrito wraps a bunch of ingredients together in real life, a burrito
Anchor<T>
wraps
T
. So I guess our vegan burrito cell becomes
Anchor<Burrito>
, a kind of ridiculous burrito burrito. Functions can transfer ours
Anchor<Burrito>
as much as they want. But when they actually unwrap the burrito to access the
Burrito
inside, we create a dependency edge in our graph, indicating to the recalculation algorithm that the cell may be needed and needs recalculation.
The approach taken by Salsa and Adapton is to use function calls and normal control flow as a way to expand these values. For example, in Adapton, we could write the Burrito for Customer cell something like this:
let burrito_for_customer = cell!({
if get!(is_vegetarian) {
get!(vegi_burrito)
} else {
get!(meat_burrito)
}
});
By distinguishing between a cell reference (here
vegi_burrito
) and the act of expanding its value (
get!
), Adapton can run on top of Rust control flow statements such as
if
. This is a great solution! However, it takes a little bit of magic global state to properly wire calls
get!
to cells
cell!
when changing
is_vegetarian
. The Incremental-influenced Anchors library takes a less magical approach. Like async-pre / await
Future
, Anchors allows launching
Anchor<T>
operations such as
map
and
then
. So, the above example would look something like this:
let burrito_for_customer: Anchor<Burrito> = is_vegetarian.then(|is_vegetarian: bool| -> Anchor<Burrito> {
if is_vegetarian {
vegi_burrito
} else {
meat_burrito
}
});
Further reading
In this already long and florid article, there was not enough space for so many topics. Hopefully these resources can shed a little more light on this very interesting problem.
- Seven implementations of Incremental , a great in-depth look at the internals of the Incremental, as well as a bunch of optimizations like constantly increasing heights that I didn't have time to talk about, plus clever ways to handle dependency-changing cells. Also worth reading from Ron Minsky: FRP Parsing .
- Video explaining how Salsa works.
- This is a Salsa ticket where Matthew Hammer, creator of Adapton, patiently explains the cutoffs to some random passerby (me) who has no idea how they work.
- Rustlab . , « » «: DX CS» — .
- , « », Materialize. , . , (!) « », , . Noira .
- Adapton .
- It turns out that this way of thinking applies to build systems as well . This is one of the first scientific articles on the similarities between build systems and spreadsheets.
- Slightly Incremental Ray Tracing is a slightly incremental ray tracer written in Ocaml.
- Just looked at "Partial State in Materialized Views Based on Data Flow" and it seems relevant.
- Skip and Imp look very interesting too.
And of course, you can always check out my Anchors framework .