For a long time mathematicians have tried to solve the problem of a grazing goat tied to a fence. But until now, they could only offer rough solutions.

Here is a simple task for you . Imagine a hedge in the shape of a circle, with a precisely known area of pasture enclosed within. You put a goat inside and tie it with a rope to the fence. How long do you need the rope for the goat to have access to exactly half of this area?
It looks like a high school geometry assignment - however, professional mathematicians and amateurs have thought about it in different formulations for over 270 years. Some variants of this problem have been successfully solved, but the riddle about a goat inside a circle has not given us anything but vague and incomplete answers.
To this day, “no one knew the exact answer to the basic question,” said Mark Meyerson., a mathematician from the US Navy Academy. "The solution has always been rough."
However, in 2020, the German mathematician Ingo Ullisch finally made progress . He found, as it is believed, the first exact solution to this problem - although it looks quite cumbersome and incomprehensible.
“This is the first accurate rope length expression I know of,” said Michael Harrison , a mathematician at Carnegie Mellon University. "This is definitely a breakthrough."
Ullisch acknowledges that his decision will not cross out textbooks or drive math revolutions. This task is isolated. "It is not related to other problems, and is not included in any mathematical theory." But there is always the possibility that such a riddle will give rise to some new mathematical ideas, or will help researchers find other approaches to other problems.
In and around the barnyard
The first problem of this type was published in 1748 in the London periodical women's magazine The Ladies Diary: Or, The Woman's Almanack [Lady's Diary, or Women's Almanac]. The magazine promised "new improvements in the arts and sciences and lots of fun little things."
The original scenario features a horse grazing on a leash in a park. In the task, the horse was tied outside the fence. If the length of the rope matches the circumference of the fence, what area can the horse graze on? Later, this task was called “outside”, because the pasture in it was not inside the circle, but outside.

The answer to the puzzle appeared in the 1749 issue. The answer was compiled by one "Mr. Heath", based, among other things, on the "research and logarithm tables" reference book. He gave the answer: 76,257.86 square yards on 160 yards of rope. And this was a rough answer, not an exact calculation. Let us explain with an example: you can write an approximate numerical answer to the equation x 2 - 2 = 0, x = 1.4142, but this will not be as accurate or satisfactory as x = √2.
The problem appeared again in 1894 in the first issue of the American Mathematical Monthly, revised for the case when the animal grazes inside the fence. This type of task is called "internal", and on average they are more difficult than external, Ullisch explained. In the external problem, you can start from the radius of the circle and the length of the rope, and then calculate the area. It can be solved through integrals.
“Solving it in the opposite direction, starting with a given area and asking what inputs lead to it, is much more difficult,” Ullisch said.
In the decades that followed, the monthly published different versions of the internal problem, mostly involving horses (and in at least one case a mule) instead of goats. There were round, square and elliptical fences. But in the 1960s, for mysterious reasons, goats began to gradually supplant horses in literature. Despite the fact that according to the mathematician Marshall Fraser, goats are "too independent to live on a leash."
Goats in the higher dimensions
In 1984, Fraser got creative with taking the problem from a flat pastoral theme to a more complex landscape. He calculated how long a rope would be needed for a goat to graze in exactly half the volume of an n-dimensional sphere when n approaches infinity. Meyerson found a logical error in his reasoning and later in the same year corrected it, but came to the same conclusion. As n approaches infinity, the ratio of the length of the rope to the radius of the sphere tends to √2.
Meyerson noted that this seemingly more complex way of describing the problem, in a multidimensional space instead of a field with grass, actually made it easier to find a solution. "In an infinite number of dimensions, we have an exact answer, and in two dimensions, such a clear solution does not exist."
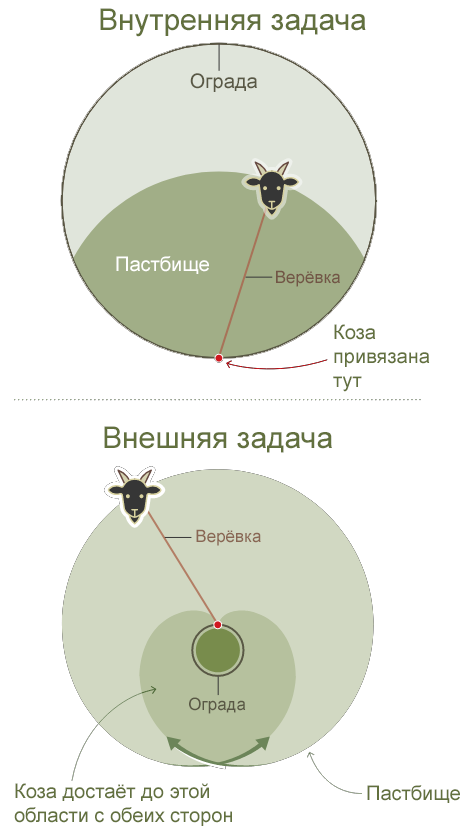
There are two types of problems for a grazing goat. Both are associated with a goat tied to a round fence. The internal version asks about the length of the rope that will give access to exactly half of the enclosed area. Outside asks what area the goat has access to given the length of the rope and the radius of the fence (in the picture, the length of the rope is equal to the circumference of the fence).
In 1998, Michael Hoffman, another mathematician at the U.S. Naval Academy, expanded the problem in a different direction when he stumbled upon an example of an outer problem on a newsgroup. In that version, it was necessary to estimate the area available to a bull tied to the outside of a circular silo. The problem interested Hoffman, and he decided to generalize it not only to a circle, but to any smooth convex curve, including ellipses and even non-closed curves.
“When faced with a problem statement for a simple case, a mathematician will try to figure out how it can be generalized,” Hoffman said.
Hoffman considered the case in which a harness of length L is less than or equal to half the length of the curve. First, he drew a tangent line where the rope is tied. A bull can graze in a semicircle with an area of πL 2/ 2 bounded by a tangent. Hoffman then calculated the exact area between the tangent and the curve through an integral.
Later, Graham Jameson , a mathematician at the University of Lancaster, and his son Nicholas came up with a detailed solution to an internal problem in three dimensions. They chose this occasion because it was less popular. Because goats cannot move in three dimensions so easily, the Jameson dubbed this task the “bird problem” in a 2017 paper . It sounds like this: if you tie a bird to a spherical cage, how long should the rope be to limit its movement to exactly half its volume?
“The problem in three dimensions is actually easier to solve than in two,” said Jameson Sr. As a result, the couple came up with the exact solution. However, since the mathematical form of the answer was, according to Jameson, "accurate but terrible" and could scare off inexperienced researchers, they also came up with a rough calculation method that gives a numerical estimate of the length of the rope, which would "please bird lovers."
Get the goat
Nevertheless, the exact solution of the two-dimensional problem in the formulation of 1894 eluded mathematicians - until the appearance of Ullisch's work in 2020. Ullish first heard about this task from a relative in 2001, when he was still a child. He began working on it in 2017, receiving his doctorate from the Wilhelm University of Westphalia in Münster. He decided to try a new approach.
By that time, it was well known that the goat problem could be reduced to a single transcendental equation , which by definition includes trigonometric terms like sine and cosine. This could create a problem, since many transcendental equations cannot be solved. For example, the equation x = cos (x) has no exact solutions.

Ingo Ullish
However, Ullisch formulated the problem in such a way as to provide himself with a more compliant transcendental equation: sin (β) - β cos (β) - π / 2 = 0. And although it too may seem inaccessible, he realized that it can be approached using a complex analysis - a branch of mathematics that applies analytical tools to equations with complex numbers. Comprehensive analysis has been around for centuries, but Ullish, as far as he knows, was the first to take this approach to hungry goats.
With this strategy, he was able to turn his transcendental equation into an equivalent expression for the length of the rope that would allow the goat to graze in half of the confined area. That is, he finally answered the question using precise mathematical formulas.

The solution to the problem is given in the form of the cosine of the ratio of two curvilinear integrals (formula from Wikipedia)
Unfortunately, there is a catch. Ullisch's solution is not some simple expression like the square root of 2. It is such a complex thing as the ratio of two curvilinear integrals mixed with different trigonometric functions. From a practical standpoint, it won't tell you exactly how long a goat's leash should be. To get an answer that is applicable to agriculture, you still need to do some rough calculations.
But Ullish still thinks the exact solution is valuable, even if it is not so beautiful and simple. “If we only use numerical values or approximations, we will never understand the essence of the nature of the solution,” he said. "The formula gives us an understanding of how the solution is derived."
Don't give up the goat
Ullisch has put the grazing goat aside for now, as he is not sure where to go next. But other mathematicians are already developing their own ideas. Harrison, for example, is preparing a paper for publication in Mathematics Magazine, where he explores the properties of a sphere in order to approach a three-dimensional generalization of the goat problem.
"In mathematics, it is often useful to come up with new ways to get an answer - even for problems that have already been solved," Meyerson noted, "since it may be possible to generalize all this for use in other problems."
This is why mathematicians have spent so much ink on imaginary animals. “My instincts tell us that working on the grazing goat problem won't give us any breakthroughs,” Harrison said, “but you can't know for sure. New mathematics can come from anywhere. "
Hoffman is more optimistic. Ullisch's transcendental equation is related to the transcendental equations that Hoffman studied in a 2017 paper . He, in turn, became interested in them thanks to the work of 1953, which exhibited conventional methods in a new light. This approach reminds him of how Ullisch applied well-known methods in complex analysis to transcendental equations in new conditions - in this case, in the problem of progoses.
"The people who make fundamental breakthroughs in mathematics are not responsible for all progress," Hoffman said. "Sometimes it goes by the fact that someone studies the classical approaches and finds in them new methods of solving the puzzle, which in the end can lead to new results."