
The reaction to the work "Formula for solving an equation of degree 4" published on January 12, 2021 on Habré , indicated that the article was not well structured methodically. Formulas could not stand up for themselves.
I'll try to fix the situation.
So, the equation is 4 degrees.
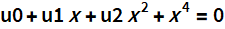
First about the Ferrari method.
The Ferrari method is remarkable in that it captures the essence of the 4th degree equation. Isolation of perfect squares leads to the appearance of a cubic resolution. As a result, the equation can be represented as a product of two square polynomials.
For an equation of 5 and 6 degrees, the technique associated with the selection of complete squares or cubes very quickly ends in nothing. It seems to me that it is precisely this circumstance that actually gave rise to the thesis about the impossibility of solving equations in radicals above degree 4.
Resolvent equation:
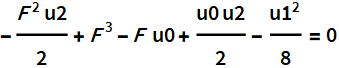
The product of two square polynomials obtained by the Ferrari method.

Coefficients of the expression on the right side of the identity.

Next, we substitute the expression for F ^ 3 from the resolvent and obtain the original polynomial of degree 4.
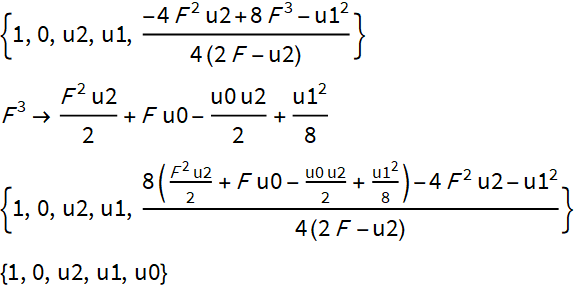
The only thing to note is that the resolvent appears only when calculating the intercept.
The roots of the same equation must be identical no matter what method is obtained.
In practice, depending on the method used, roots are obtained, about which in their symbolic representation it is difficult to say whether they are identical or not. Why not have another solution method, which in some cases gives simpler symbolic representations of roots. This possibility is important when choosing the values of the parameters of the roots and conjugating the roots of several equations.
Differences between the ftvmetrics method and the Ferrari method:
- other auxiliary equations (resolvents);
- auxiliary equations "work" not on the free term, but on the coefficients at the first and second degrees;
- it is possible to calculate two roots of the 4th degree equation from a cubic equation, presented in canonical form.
First solution.
It was given in the article named at the beginning.
Auxiliary equation

The product of quadratic polynomials, which is identical to the 4th degree equation after repeated replacement R ^ 3

Instead of solving each of the quadratic polynomials indicated above, in the ftvmetrics method you can find the roots of the cubic equation.Two

of them will be the roots of the 4th degree equation.
In this case, it becomes possible to express the roots in terms of exponentials or trigonometric functions.
You can make sure that the alternative equation is correct by calculating the subresultants and checking the first two values.
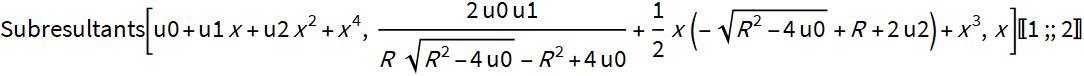
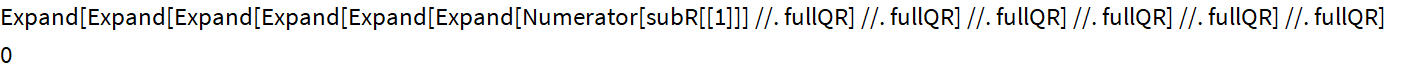

The resulting expressions of the subresultants are "brutal", but when you know what you are looking for, everything is not so sad.
Second solution.
The auxiliary equation
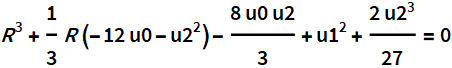
has a canonical form.
The product of quadratic polynomials, identical to the equation of degree 4 after repeated replacement R ^ 3. The

correctness of the alternative equation is also checked through subresultants.
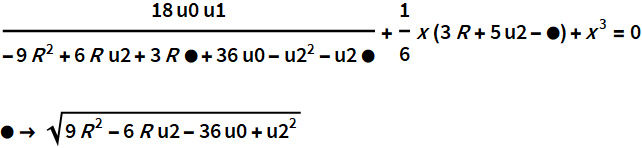
In the second solution, the auxiliary and alternative equations have a canonical representation.
It's curious to get something new after 400 years.
Send interesting business tasks to Direct Instagram .