
A post about calculating the distance to the Sun prompted another text - about calculating the distance to the Moon (since this figure was used by Aristarchus in his calculations, the question arose, where did he get it from). But already in the comments to the second text, the following question was asked - "And now can you tell us more about the Earth's radius?"
Asked - we answer. Well, in order not to "get up twice", I will start not even with the radius, but with how the Greeks came to the conclusion that the Earth has the shape of a ball, not a disk or a chest (as the Byzantine scientist Kozma Indikoplov later argued).
It was the Greeks who took care of this issue, in more ancient civilizations (Babylon, Egypt) they studied the sky, and quite carefully, tried to predict the movement of heavenly bodies, but they did not bother with the question of the shape of the Earth.
It is difficult to say which of the Greeks was the first to voice the idea that the Earth is a ball, the most common version is that Pythagoras . But the oldest written treatise with this statement that has come down to us ("On a Moving Sphere") belongs to another mathematician - Autolycus of Pitana, who was born two hundred years later than Pythagoras. True, this is generally the oldest ancient mathematical treatise that has come down to us. And already in it, the Earth is called a sphere. But there it was presented as a given, i.e. Autolycus was not the first to come up with this idea.
And then his contemporary the great Aristotle, in his treatise On Heaven, substantiated this statement in detail . Basically, the explanations were of a philosophical nature (the spherical Earth is the indestructible center of the cosmos, etc.). But there was also a number of very specific proofs. First of all, the results of observations of lunar eclipses: they always have an arcuate bounding line. “Since the Moon is eclipsed because it is obscured by the Earth, then the reason for this shape is the circumference of the Earth, and the Earth is spherical,” Aristotle concludes.
He drew an even more interesting conclusion from observations of the stars. To begin with, the philosopher noted that in Egypt and in Macedonia there are differences noticeable to the observer in the arrangement of the stars. And he deduced: "From this it is clear not only that the Earth is round, but also that this sphere is small: otherwise, such insignificant displacements would not cause such rapid changes."
Well, then, since the educated part of the Greeks decided on the shape of the Earth, as well as the fact that its dimensions are not so great, the next step suggested itself - to measure the Earth.
Before moving on to the process and its results, I would like to note one nuance. The Greeks measured, as I said in stages, but the nuance is that it is now a kilometer and a kilometer in Africa. And then there was no SI system. Each stage is 100 pairs of steps or 600 feet, but steps and feet in different systems of measures could differ slightly: there were several options for stages, from 172 to 185 meters (and also the Babylonian version of the stage, but we are not interested in it here). You often have to guess what stage this or that author used. Therefore, when we translate the results into the usual kilometers, then, of course, we run the risk of making mistakes. But - within 6-7%. For astronomy it is a lot, for the history of the question it is tolerable.
Now, actually about how the Greeks measured the Earth. Two studies are known for this purpose. The first was carried out by Eratosthenes in the 3rd century BC, the second - by Posidonius a little over a hundred years later. In both cases, the Greeks took a similar approach, the difference was in the details. Its meaning is as follows: both the Sun and the stars are available for simultaneous observation in different places on Earth, but since the distance to them is clearly many times larger than the dimensions of the Earth itself, we can consider all the rays of light coming from them to us parallel.
Eratosthenes measured the height of the Sun above the horizon at noon of the summer solstice in Alexandria and Siena (Aswan). Why there? And even before him, the ancient Egyptians noticed that during the summer solstice the sun illuminates the bottom of deep wells in Siena (now Aswan), but not in Alexandria. If the Earth were flat, Eratosthenes reasoned, this could not be (we remember - the rays are parallel), but it is round, i.e. curved. And Siena and Alexandria are on the same meridian (he believed) at a distance of 5000 stades from each other. This means that the walls in Alexandria are tilted at a certain angle in relation to the walls in Siena, so at noon of the solstice they continue to cast some shadow.
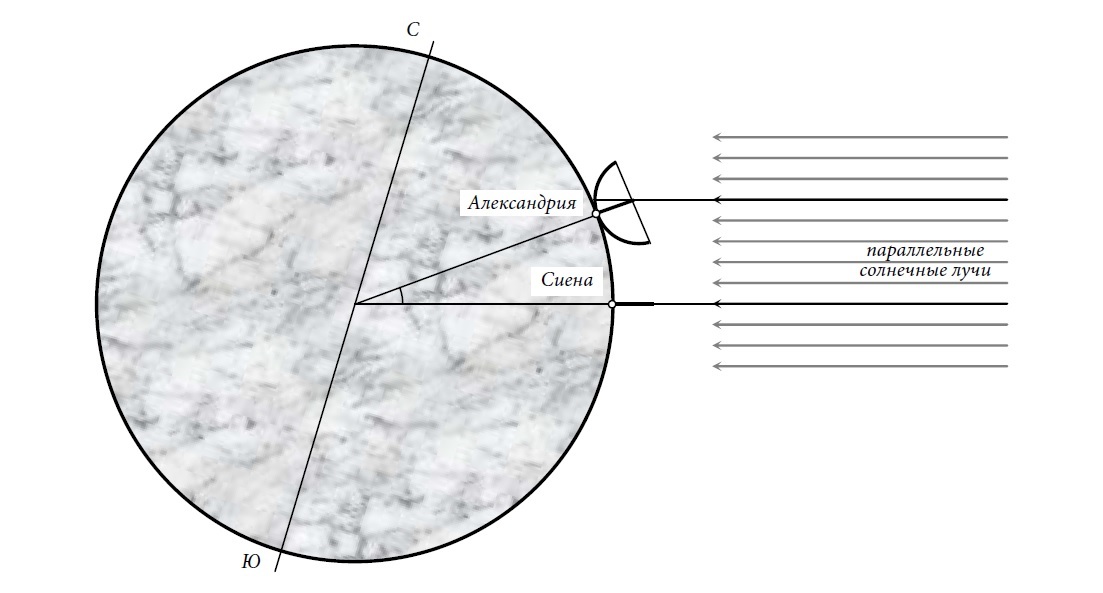
Eratosthenes measured the shadow from one of the Alexandrian obelisk, knowing also its height, he “built a triangle from the obelisk and its shadow” and calculated that the angle of deflection of the obelisk from the sunbeam is just over 7 degrees. This meant that Alexandria was 7 degrees from Siena along the earth's circumference. Such an angle is 1/50 of a circle and at the same time the mentioned 5000 stades. Hence the total circumference of 250,000 stades, concluded Eratosthenes. And the Greeks knew how to calculate the radius, knowing the circumference.
Today we know that the calculations of Eratosthenes had a number of serious errors: Alexandria and Siena are not located on the same meridian, therefore the difference between their parallels is less, this distance itself was also measured approximately, according to the caravan men, and the angles of these cities towards the sun's rays he measured with an error. And yet, he managed to get a result very close to modern data (6 371 km). True, depending on what stages he considered, if Greek, then yes, his answer is 6 916 km, and if the stages of the Egyptian pharaohs (it was in Egypt and the distance could be indicated in them), then his answer is 8 397 km is much more real.
However, Posidonius confused even more. But he counted not by the shadow of the Sun, but by the location of the star Canopus in the sky of Alexandria and the Greek island of Rhodes, which were separated by the same 5000 stadia. But these points also did not lie on the same meridian, plus the Greeks measured sea distances with much less accuracy. As a result, according to his calculations, the Earth turned out to be almost a third less than that of Eratosthenes.
Yes, the Greeks were mistaken in their calculations, but the main thing they did was to come up with a method for measuring the size of the Earth without leaving its surface. Then it was about improving geographic data and measuring instruments. Well, the Greeks did not stop and figured out how to calculate the distance to the Moon and the Sun.