It is usually believed that a quantum measurement affects the measured object - it goes from an indefinite state to a certain one, as in quantum physics a superposition of states "collapses" into a single eigenstate. However, few people think about the fact that measurement can also destroy quantum information.
Imagine yourself in the shoes of a scientist trying to understand reality at a fundamental level. How would you deal with this issue? You would be trying to break down matter into tiny components that are easier to study. You would design experiments to test and measure the properties of these tiny subatomic particles in various states. If you were really smart, you would try to use the properties you measured to understand the laws of the universe.
You might well decide that with enough measurements, or enough experiments, you can find out anything you want about any particle (or group of particles) in the entire universe. Similar expectations were common among scientists at the dawn of the 20th century. But it turned out that the quantum universe has other proposals for us. Certain measurements completely negate the information you received in previous measurements. Apparently, the act of measuring does destroy information. And this is how we found out.

Certain mathematical operations, such as addition or multiplication, do not depend on the order of actions - they are commutative. If the order of the operations matters, and the result depends on it, then the operations are called non-commutative. In the world of physics, this is very important.
In theory, the story begins with a simple mathematical idea: the concept of commutativity. Commutativity is when you can rearrange parts in places without changing the result. Addition is commutative: 2 + 3 = 3 + 2. The same is true for multiplication: 2 × 3 = 3 × 2. Subtraction is not commutative: 2 - 3 ≠ 3 - 2; you need to add a minus to the right for the expression to become true. Division is also not commutative, and with it everything is a little more complicated: 2 ÷ 3 ≠ 3 ÷ 2; one of the parts must be inverted in order to make it equal to the other.
In physics, commutability refers not only to mathematical operations, but also to physical manipulation or measurement. A simple example: rotations. We can take an object that is different in all three dimensions - for example, a cell phone - and do two rotations one after the other:
- holding the object in front of you, rotate it 90 ° counterclockwise relative to the axis directed at you;
- rotate the same object 90 ° clockwise around the vertical axis.
It may surprise some that the order in which these spins are performed matters.

The author's previous phone, from the era before smartphones, illustrates the non-commutativity of rotations in three-dimensional space. The top and bottom rows, from left to right, start at the same position. At the top, following a 90 ° counterclockwise rotation in the plane of the photograph, a 90 ° clockwise rotation around the vertical axis follows. At the bottom, the same two turns are made in a different order. The non-commutativity of rotations is obvious.
The idea of non-commutativity appears even in the world of classical physics, but its most famous application relates to the quantum world in the form of Heisenberg's uncertainty principle... In our classical world, we can measure many properties of an object at any given time. Place an object on the balance and measure its mass [weight / approx. per.]. Attach a motion sensor to it and measure its momentum. Shoot it with a laser and measure its location. Send it to the calorimeter and measure its energy. Start the timer while the object is wobbling and get the wobble period.
In the quantum universe, many of these measurements are valid, but only the moment you make them - and not forever. The point is that certain quantum properties that you can measure - pairs of quantities called conjugate variables - are related to each other. If you measure momentum with a certain accuracy, you cannot know the location of a particle more accurately than with a certain error - even if you previously measured this location much more accurately.
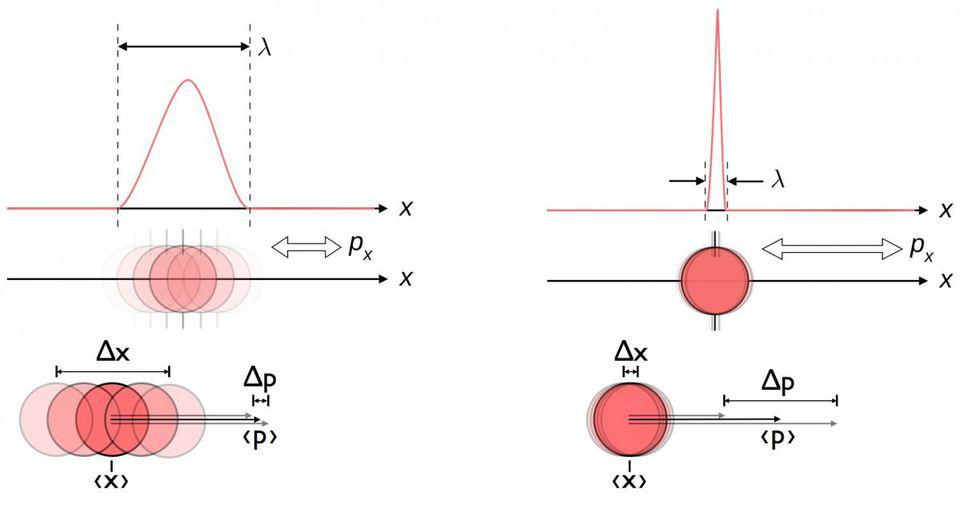
The inherent uncertainty of the quantum world between location and momentum. The better you know the location of a particle, the less you know its momentum - and vice versa. Location and momentum are better described by a probabilistic wave function rather than a single value.
Many have found it hard to accept the uncertainty principle, and yet the universe seems to support it. It also applies to other pairs of conjugate variables:
- location (Δx) and momentum (Δp),
- energy (ΔE) and time (Δt),
- electric potential, or voltage (Δφ) and free electric charge (Δq),
- angular momentum (ΔL) and orientation, or angular position (Δθ).
However, if you really need to demonstrate a physical necessity, you have to get experimental evidence to support it. It is not enough to simply say “I don’t know how accurate my measurements are”. You need to find a way to show that the information you received in previous measurements with a certain accuracy was destroyed by the subsequent measurements.
And in 1921, physicist Otto Stern came up with an ingenious way to test this.

Individual and composite particles can have both orbital and intrinsic (spin) angular momentum. When these particles have an intrinsic or intrinsic electrical charge, a magnetic moment appears that causes them to deflect a certain amount in the presence of a magnetic field.
Let's say you have a quantum particle - an electron, a proton, a composite nucleus (an object consisting of bound protons and neutrons), or even a neutral atom with a nucleus and electrons revolving around it. Such an object has several quantum properties inherent in it: mass, electric charge, etc. In theory, it should also have an angular momentum - not only due to the fact that it revolves around other particles (or other particles revolve around it), but also some inherent, internal angular momentum. This quantum property of an object is called spin [to spin (English) - to rotate / approx. per.], by analogy with a top rotating around its own axis.
If you imagine a top, then you can immediately come up with two ways to rotate it:
- clockwise around the vertical axis,
- or counterclockwise.
Living in a world without gravity (and without preferred directions - which role, in our case, is played by the direction to the center of the Earth), one could imagine its rotation clockwise or counterclockwise around any axis in all three dimensions. This is our premise: the idea that particles have a spin, an internal angular momentum. Although in 1921 there were still several years before George Eugene Uhlenbeck and Samuel Abraham Goudsmit formulated their hypothesis of the electron spin, this idea was still present in the "old quantum theory" of Bohr and Sommerfeld.

The trajectory of a spinning quantum particle passing through a magnetic field is affected by its magnetic moment associated with its spin. In quantum theory, this means that the spin must be discrete.
How to measure the spin of quantum particles? How to determine whether spin is a continuous quantity that can take on any value in the manner of classical parameters, or is it inherently quantum and discrete?
Stern guessed that if we take a magnetic field perpendicular to the direction of motion of a charged particle with spin, the field will act on the trajectory of motion in accordance with the magnetic moment associated with the spin. A particle without a spin will not be affected, but a particle with a spin will deflect in the direction of the magnetic field.
If the spin is discrete, i.e., quantized, all particles moving at the same speed must be in the same place. If the spin is classical and continuous, the particles can be anywhere.

A beam of particles passing through a magnet can give quantum / discrete results (5) for the angular momentum of the particles, or classical / continuous (4). The Stern-Gerlach experiment has demonstrated the existence of several important quantum phenomena.
In 1922, physicist Walter Gerlacharranged a test of Stern's ideas by developing an experiment. Gerlach started with an electromagnet through which a beam of silver atoms travels, which can be easily accelerated to the same speed. When the electromagnet was turned off, all the silver atoms hit the same spot on the detector on the other side of the magnet. When the magnet was turned on, the beam split into two parts - half of the atoms changed their trajectory, deviating in one direction, half in the other. Today it is known that this behavior corresponds to the presence of spins +1/2 and -1/2 directed parallel or antiparallel to the magnetic field lines.
This early experiment was enough to prove the existence of spin, which is quantized into discrete values. However, further the ability of quantum mechanics to destroy previously obtained information was demonstrated. When silver atoms pass through the Stern-Gerlach apparatus with the magnetic field turned on, the atom beam is split into two, in accordance with the spins of the particles.
Okay - what if we pass one of the halves of the beam through another Stern-Gerlach apparatus?

If you shoot particles through the Stern-Gerlach apparatus, the magnetic field will split their beam into two parts, in accordance with the possible spin options. If the second Stern-Gerlach apparatus is placed in the path of one of the halves of the beam, splitting will no longer occur, since this quantum property of particles has already been determined.
The answer may surprise you: it all depends on which direction the magnet is oriented in. If the first Stern-Gerlach apparatus was oriented, say, along the x-axis, then some of the particles will go in the + x direction, and some - along the –x direction. Let's concentrate on the first. If you pass them through another magnet oriented along the x axis, the particles will not separate - they will all remain oriented in the + x direction.
But if you orient the second magnetic field along the y-axis, the result may surprise you. Now the beam of particles, initially oriented in the + x direction, will split along the y-axis: half will go in the + y direction, and the other in the –y direction.
Then comes the critical moment: what happens if we concentrate only on particles + y, and again pass them through a magnetic field oriented along the x axis?
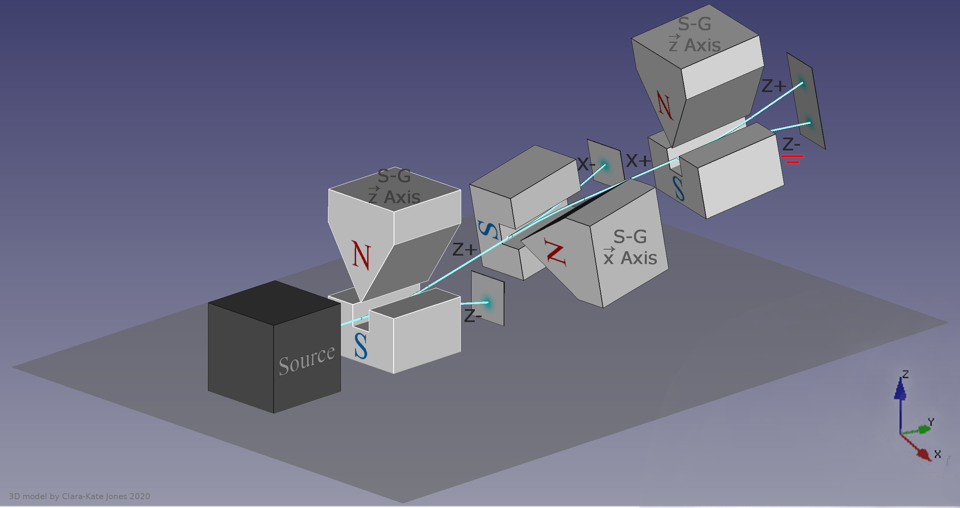
If you pass a set of particles through the Stern-Gerlach apparatus once, they will separate according to their spin. If you pass them through a second, perpendicular magnet, they separate in a new direction. If you use a third magnet parallel to the first, they will separate again - which means that the previously determined information has again become random due to the most recent measurement.
They will again, like the first time, split along the + x and –x directions. By passing them through the second magnet, oriented perpendicularly, you have destroyed the information obtained in the first measurement. Today we understand that directions x, y and z do not commute with each other. A quantum measurement of a variable of one type destroys all previous information about its conjugate variables.

Several successive apparatuses splitting quantum particles along one of the axes according to their spin will split them along the perpendicular to the previous direction, but will not split along the same direction.
The Stern-Gerlach experiment has one lasting consequence. In 1927, it was shown that splitting occurs even in hydrogen atoms, which indicates that they have a nonzero magnetic moment. Atomic nuclei have an inherent quantum angular momentum, and they also fission in the Stern-Gerlach apparatus. By changing the magnetic field over time, scientists figured out how to make a magnetic moment take one state or another. It turned out to be possible to induce transitions between states by changing the field in time. This was the birth of magnetic resonance, which is now ubiquitous in MRI machines, and eventually led to the atomic clock.

- . . . 1937 , , .
It would seem that the act of measurement and observation should not influence the result of the experiment. The idea that observing a system changes its properties seems absurd. But in the quantum universe this not only happens - it was demonstrated even before the theory was fully formed. Measuring the spin of a particle along one direction destroys the previously obtained information about the other two directions. Even if you have measured them before and know them exactly, the new dimension fundamentally erases (randomizes) any previously obtained information.
To many physicists who have heard Einstein's famous statement that " God does not play dice with the Universe“This experiment should first come to mind as a counterexample. It doesn't matter how well you think you understand reality. It doesn't matter how accurately and carefully you measure it in different ways. The new dimension does destroy the old information. All that is needed to prove this is a magnet and some particles.