
In the comments to my last post , they noted that I did not describe how the ancient Greek astronomers calculated the distance to the Moon. The following text is devoted to this topic. True, the task turned out to be simpler than with the distance to the Sun, therefore the post will turn out to be much shorter.
To begin with, ancient science had one feature: the Greeks (and then the Romans) actually did not know how to do algebra, they did not use decimal fractions, the concept of zero, even the number system for both was alphabetical, not positional. But on the other hand, they learned well how to solve geometric problems. And they cognized the world with the help of geometry.
In particular, the distance to the Moon was calculated. Just Aristarchus of Samos is considered to be the first who succeeded. And he did it as follows (I briefly outline who needs more details - read the original source, who needs a lot of formulas - this is also on the Web, for example, here ).
First, he measured the angular radius of our satellite. Knowing it, you can calculate "how many" moons can be placed in its orbit. This amount, according to the formula for the circumference, is equal to the product of the radius of the orbit (the same distance) by 2 π. Now, in order to calculate the radius, Aristarchus had to calculate not the angular, but the actual size of the moon.
Briefly, his further decision sounded like this. Eclipses proved that the Sun is farther from the Earth than the Moon, and their angular sizes are approximately equal (according to the calculations of Aristarchus). Based on this, the astronomer concluded that the sun's rays falling on the moon converge behind it to a point on the surface of the earth. Then he measured the shadow from the Earth on the lunar disk during a lunar eclipse. The shadow turned out to be twice as large as the moon itself.
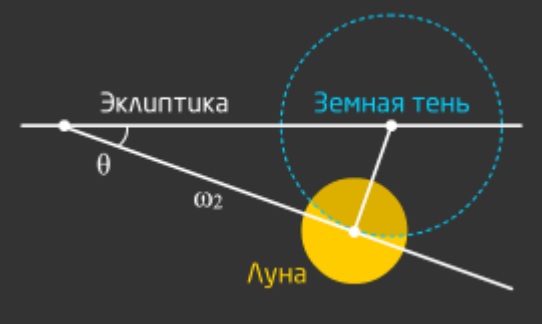
Aristarchus summarized the results of both conclusions (the difference in shadows and the "departure" of the sun's rays from the diameter to a point) and came to the conclusion that the Moon is three times smaller than the Earth. This was pretty close to the modern answer - 3.6 times.
So, Aristarchus calculated that the Moon "fits" into orbit 720 times and it is 3 times smaller than the Earth. So the Earth would "fit" in the lunar orbit 240 times. The diameter of the Earth was known to the Greeks thanks to Eratosthenes (and this was very close to the real value). Now the formula for calculating the radius of the lunar orbit was quite simple: 240 Earth diameters divided by 2 π. Aristarchus got 486400 km.
A hundred years later, another ancient astronomer Hipparchus clarified his calculations: in his answer, the Moon was placed in orbit only 650 times, and the distance was already about 382 thousand kilometers . Which is only a couple of thousand kilometers at odds with modern data.