
There are several methods for finding the roots of a polynomial equation of the 4th degree.
However, they are not very convenient for solving equations with coefficients, which are expressions with parameters.
1. Formula for solving an equation of degree 4
Consider an equation of the 4th degree, the sum of the roots of which is equal to zero. Coefficients can be real or complex.

The product of the next two squares is identical to the considered equation of the 4th degree.
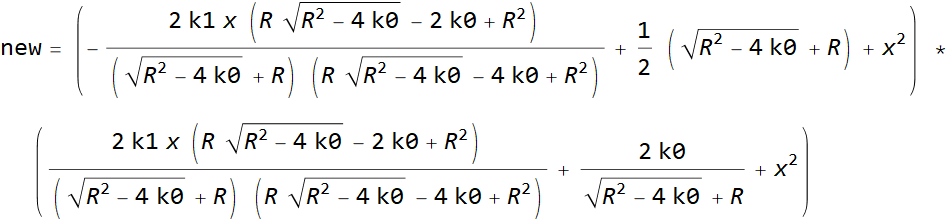
The R value is the solution to the following cubic equation.
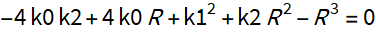
Almost the same equation appears when solving an equation of the 4th degree by expanding into the difference of perfect squares. We will call this cubic equation auxiliary.
Let's calculate the product of two squares new.
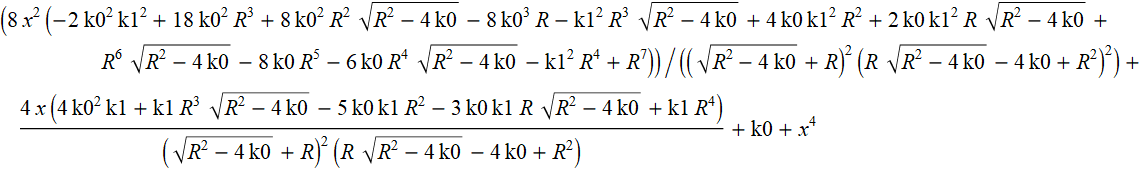
The same, but in the form of coefficients at powers of x (in decreasing order of powers).
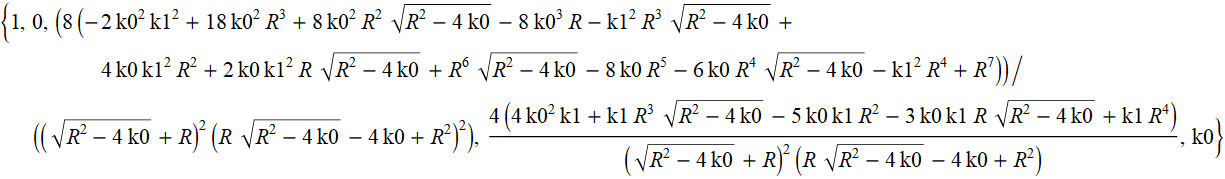
Let us simplify the expressions for the coefficients at the second and first powers of x.
The above expression is for the first degree of x.

As a result, we get k1.
The above expression is for the second power of x.

Or

Substituting the expression for R ^ 3 we get
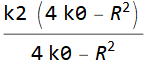
Or k2.
So, new is identical to the equation of the 4th degree, the sum of roots of which is equal to zero.
The problem with the auxiliary cubic equation remains.
Of course, traditional solution methods can be used. But then it will be necessary to transform the equation to the canonical form and separately consider three solutions depending on the values of the coefficients. This is not always convenient for coefficients that are expressions with parameters.
2. Solution of the cubic equation by the Chirnhausen transformation method
Consider the solution of the cubic equation by the not very widespread Chirnhausen transformation method.
So, we solve the original equation
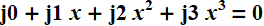
by the Chirnhausen method.
The essence of the method consists in the following transformations.
1. The equation for y is introduced
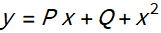
2. Both sides of the equality from item 1 are multiplied by x

Then the expression for x ^ 3 is replaced by The
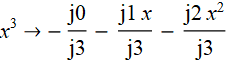
expression

In general, the transformations described in Section 2 are not identical. But if we consider only the values of x, which are the roots of the original equation, interesting, then these transformations can be considered quasi-identical. And then y is represented by an expression corresponding to the roots of the original equation.
3. For a cubic equation, the operation in item 2 is performed one more time. As a result, a system of 3 equations in x is obtained, which has three nonzero solutions corresponding to the roots of the original equation. From the coefficients x we form the matrix
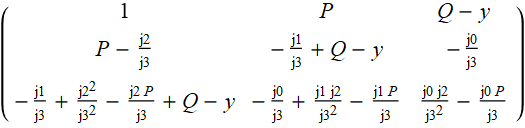
4. Find the determinant of the matrix, which is represented by a cubic expression in y.
We calculate the values that ensure the equality of the determinant to zero.
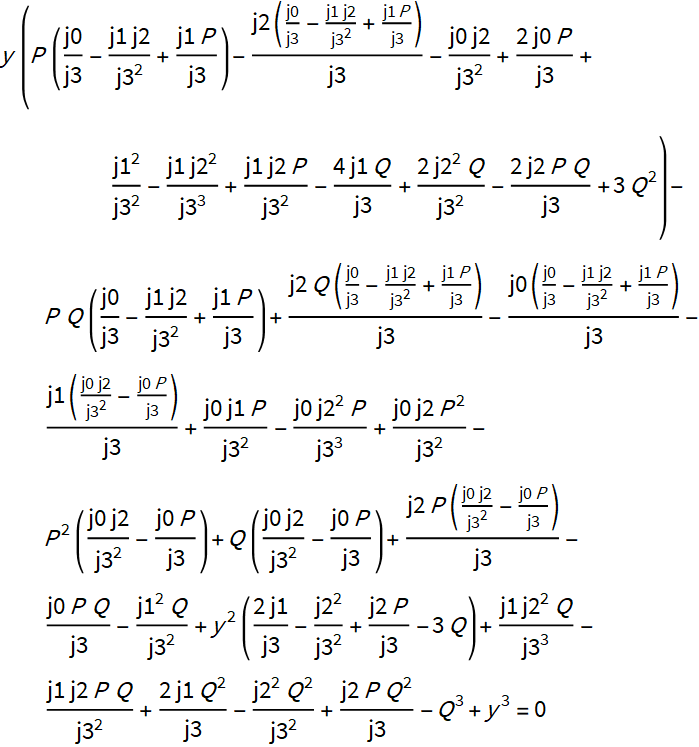
5. In the equation for y there are two parameters P and Q. Let's calculate them so that the coefficients at the second and first degrees of y are equal to zero.
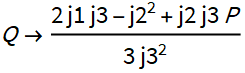
Any P

, where

6. As a result, we have an equation with three multiple roots for y

7. It remains to solve a quadratic equation with known y, P, Q
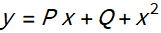
One of the solutions will be a solution to the original equation.
3. Parameters for solving the auxiliary cubic equation
For specific values of the coefficients, everything does not look so scary.
Note that only one root R of the auxiliary cubic equation is required for the formula for solving the 4th degree equation.
For specific coefficients of the auxiliary equation, we have

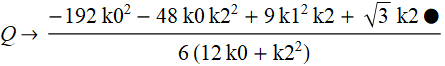
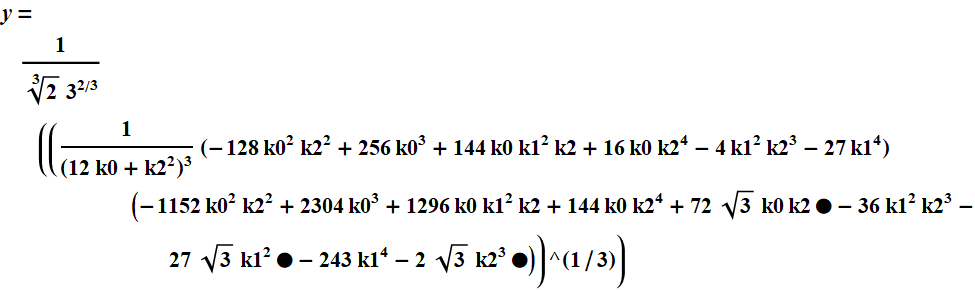

When using the formula for solving an equation of the 4th degree, it is necessary to refer to - "Method ftvmetrics".
Send interesting tasks to Direct Instagram .