When I was studying at the institute, I really did not like philosophy. The point is not only that it was then a Marsist-Leninist philosophy - I just did not see the point in this senseless pile of words. Much later I discovered that I was fond of precisely philosophy - but the philosophy of science.
In my opinion, philosophy should have a specific object of consideration: infinities in set theory, transfinite numbers, theories and provability, Max Tegmark's hypothesis of the mathematical universe. And then there is real progress (for example, Gödel's theorem), and the words simply fit the frame given by the specifics. Otherwise, it turns out an attempt to build a structure from liquid semolina, some kind of intellectual masturbation.
Georg Cantor, who laid the foundation for set theory and discovered the difference between the types of cardinalities (in English, cardinalities), is, in my opinion, a much greater philosopher than Kant and Hegel. You may not take a spoon out of your cup of coffee when you drink it and eat an apple with a stub, but you must know the difference between a countable set and a continuum if you are involved in IT or any technical field.
One of the philosophically interesting things is the famous (in narrow circles) Axiom of Choice (AC) - seemingly completely harmless, but with monstrous consequences. The axiom states that if there are two non-empty sets, then there is also a set containing exactly one element from both:
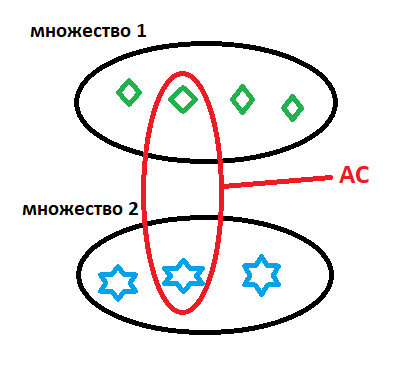
If one of these sets contains only one element, then it will always be selected and work like a hook, "fetching" elements from the second set. If after each such act of choice we will remove the selected elements, then using this procedure we can parse any set by elements .
Paradoxes Axioms of Choice
, "" , " ". , , ( ). , (, ) . .
, . intangibles - , , . .

, - ! ? . , , - . , . !
, . , , . AC , . , , . "" AC (, ), , , .
- , , . , , . . , , . - .
, [0,1]. , , , '0.324443', '1/3', '1/pi' (pi ), 'min ...' ( , ). , , ... , , . , , !
, , :

( ), . ' ' . - ( ) ( - ). ( , ?) - !
:

. -! , , , . :

, . , ?
, , ,
, (
)
- 'one level up' :
,
. ,
. , .
, /
. - - , . . (one level down) ' , ' , ( )
() , . . , , , , , . , , , , '' .
Cognitive Closure
, , -. . ' ' . , , . . , , .
. , :
, , , ' ' (, , ). , ' ',
- . , '' - .
( )
New mysterianism
- , . . , . ( ? , )
, cognitive closure - fixed points. . 1,2,3, ... 5556054, , . . , ' ' - , , .
It is important that the cognitive closure is not visible from below as a border. This is not a barrier. This is not a difficult task that you cannot solve. You don't see it at all - everything is as it were, you can write another article , investigate another phenomenon , prove another theorem . Nobody will stop you - you simply cannot understand what you are not able to understand. You won't see the problem.