The curse of Tsiolkovsky and the grace of Obert

Hello, dear readers of Habr.



We continue to study orbital mechanics on a finger and two energies. In this article, you will learn about the Tsiolkovsky formula, the Obert effect, how energy differs from momentum, how rockets work, and all this using the simplest examples with a strong 90-degree geometry.

The Aubert effect

Let's start with the Aubert Effect, although this is an extremely complex effect, but having dealt with it, we will understand all of orbital physics. First, let's ask ourselves a question - What is the strength, brother? - In horse power!



How much horsepower does a rocket motor have?



The answer is strange - in different ways, the same kilogram of fuel in the same engine gives a different amount of energy. The reason is the different speed at which this fuel is used, the higher the speed of the rocket itself, the more energy the engine gives, and the same engine accelerating sideways (relative to the current speed) will give less energy than when accelerating forward.



Let's look at 2 good and illustrative examples right away. One from YouTube from garage scientist Igor Beletsky, who demonstrated the Obert effect with a syringe, rubber band and something else, and the second example from Wikipedia.

Handicraft experiment.

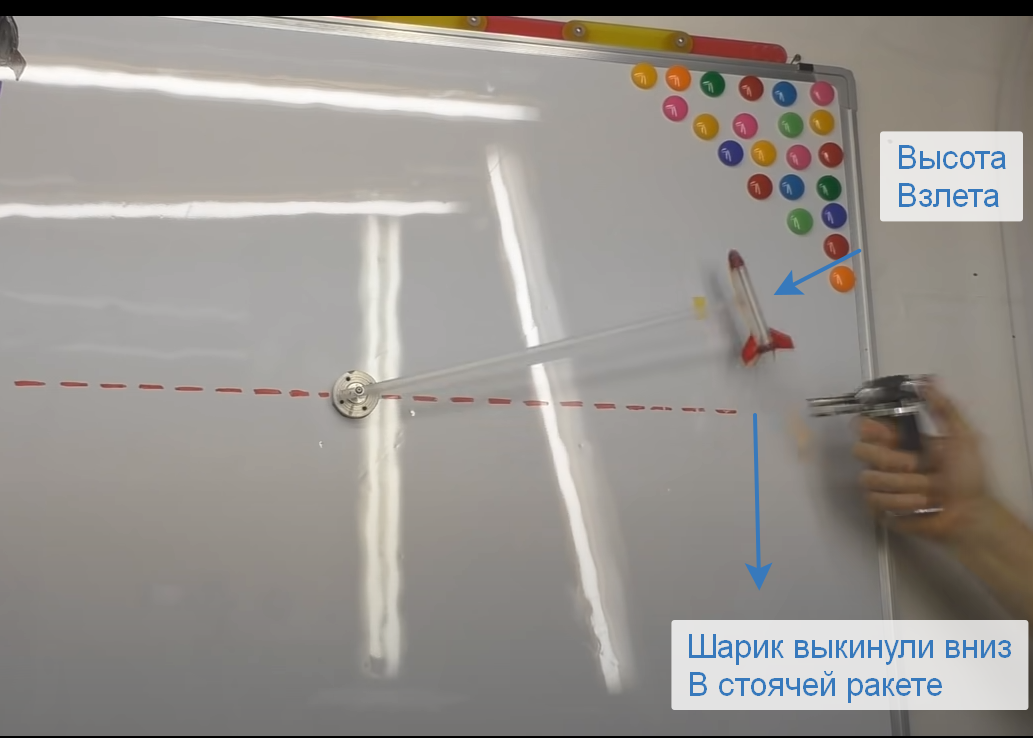
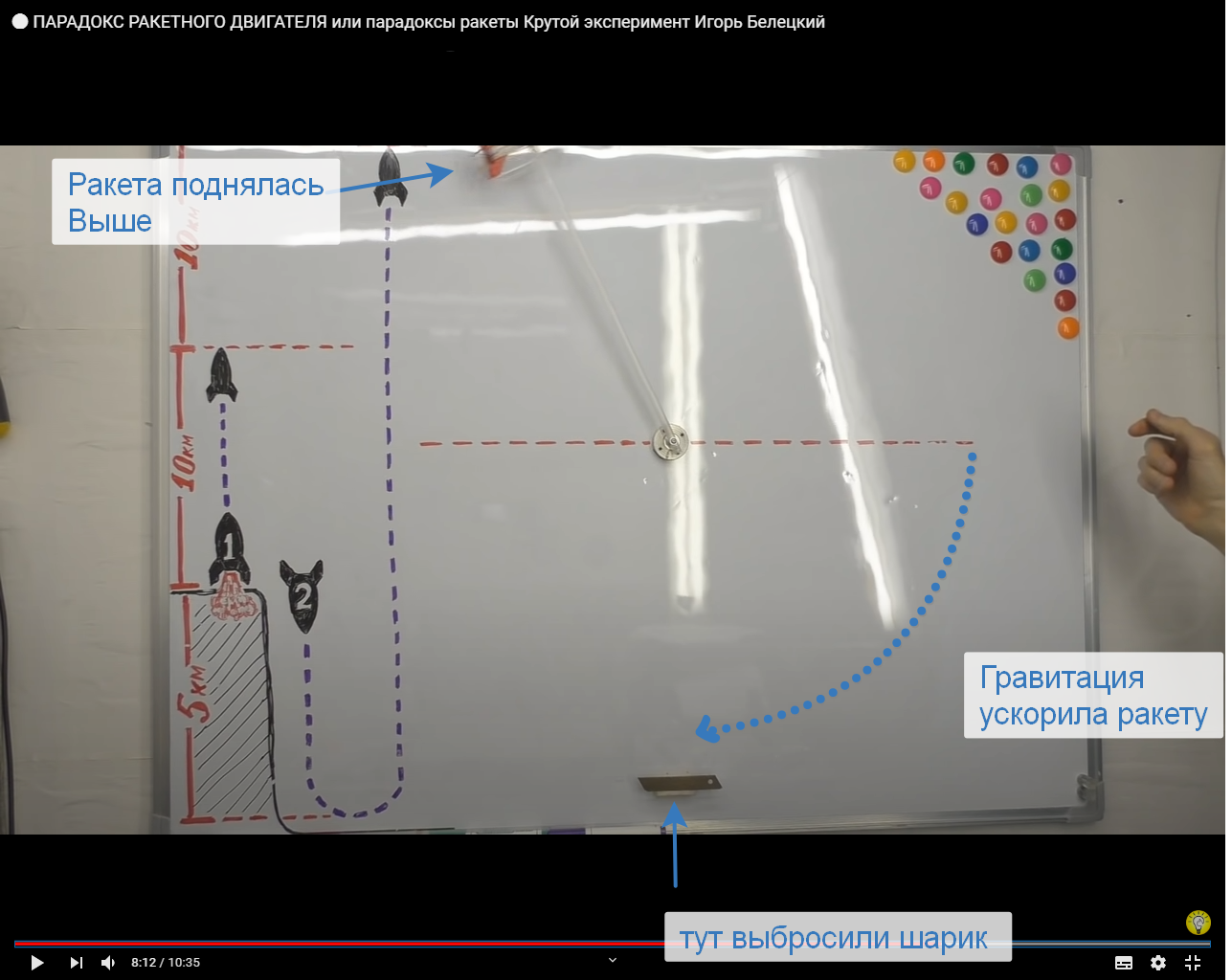
Source: Igor Beletsky's YouTube channel

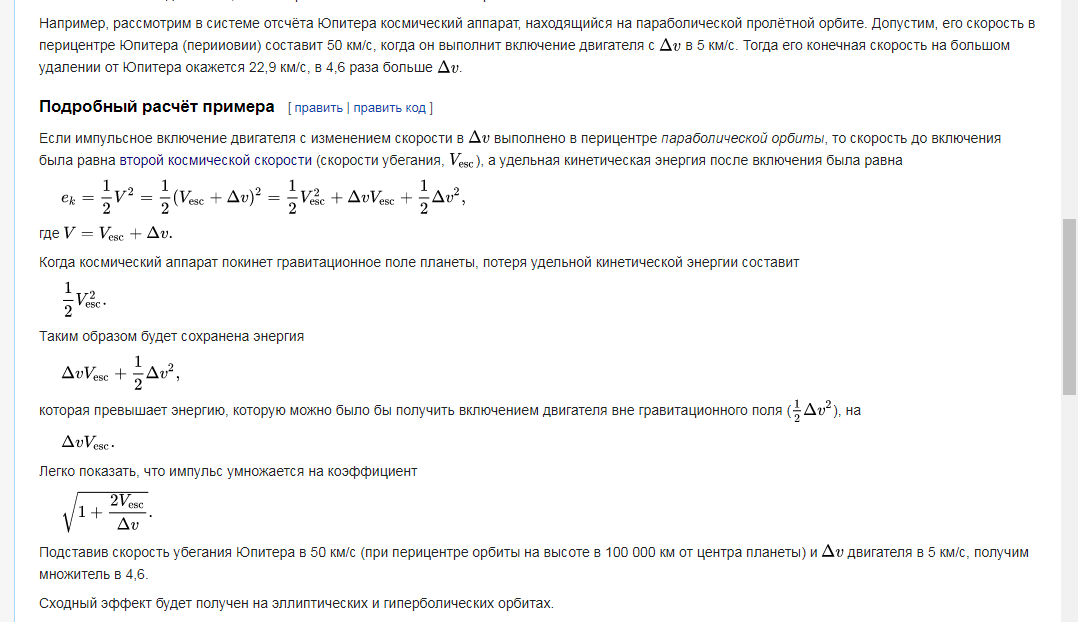
From Wikipedia

In a video from YouTube - you can even see this effect with your own eyes, in order to understand why this is happening, let's consider kinetic and "thermal" energy separately.



All we need to know about kinetic energy in the context of orbital mechanics is Newton's third law: - The force of action is equal to the force of reaction F = -F. Those. If we throw something forward at a speed of 10 m / s, then something will necessarily fly in the opposite direction with the same speed of 10 m / s (with the same masses).



And we also need the formula for the energy itself $$$E=\frac{mv^2}{{2}}$ (mass * speed squared / 2), so as not to bother with constant division by 2, I will always take a mass of 2 kg. - then the energy will be equal to just the speed squared. For example, at a speed of 10 m / s, the energy is 10 * 10 = 100 Joules (for every 2 kg.).



So let's imagine a cannon on wheels that rolls and we will accelerate the cannon with shots. We take the mass of the kernels 2 kg. It shoots at a speed of +1 m / s (weak, of course, but it's convenient to count). Let's say the cannon rolls at a speed of 2 m / s and shoots in the opposite direction - i.e.



The cannon core before the shot had a speed of 2 m / s and its energy was 2 squared = 4 joules, after the shot its speed became 1 m / s and the energy was 1 J. - that is, after the shot, the core lost 3 J, and the cannon accordingly received this energy. We will not count the mass and speed of the gun, something else is important to us.



Now imagine that the cannon moves 3 m / s, before the shot the core has an energy of 3 squared = 9 J, and after the shot 2 squared = 4 J, that is, this time the nucleus has already lost 5 joules, etc. the higher the speed of the cannon, the more energy the core loses. So gunpowder gives more energy? - No, the energy gain from each shot increases, but where does the initial velocity of the cannon come from? From the same shots, and so that we have 1 core at a speed of 4 m / s, we need to shoot 5 cores at a lower speed (the number 5 is from the ceiling, but you get the meaning) - that is, additional energy is taken from the previous shots. Now let's see how the gunpowder itself works.

How gunpowder creates momentum

Although let's not take her childhood away from poor Greta, and take an Orthodox Catholic solar panel, charge the batteries and consider energy in a form that is more understandable to a modern person. Electricity is measured in Watts, and 1 Watt = 1 Joule (they have different physical meaning, but the bottom line is the same = acceleration = to accelerate 2kg. To 10m / s, 100 Watts = 100 J. are needed.)



Now we take a spherical wheel in vacuum with 2- with weights on the edges, we begin to spin with an electric motor and throw the weights in different directions. The weights are, as always, 2 kg, the wheel itself is not interesting to us and we will consider the energy spent only on untwisting the weights. Let's spin them up to 10 m / s, for this we need 10 * 10 = 100 W for each load.







Everything is simple here, spent 200 watts = received 2 loads at a speed of 10 m / s in opposite directions. Now let's add the speed to the wheel itself = 10 m / s.







And here we see an interesting picture.



To unwind, we also spent 100 J for each load = 200 J. +200 J. Each load had initially (they both moved with the wheel of 10 m / s).



The accelerated load doubled its speed and flew out at a speed of 20 m / s, and its energy increased 4 times - up to 400 J. - in fact, it took away all the energy in general - both +200 spent on untwisting both of them, and the energy of the load which slowed down - another +100 J. (+100 he had initially) - The law of conservation of momentum is a very impudent law - the accelerated one takes everything. Rather, the efficiency during acceleration increases from 50% at zero speed to 100% at an ejection speed equal to the speed of the wheel itself.



The same thing happens in a rocket that burns / ejects fuel at a speed of ~ 3,000 m / s and with acceleration the engine efficiency increases, but to enter a circular orbit, a minimum speed of 7,900 m / s is needed and let's see what happens if the speed of the wheel itself is more ejection rate.







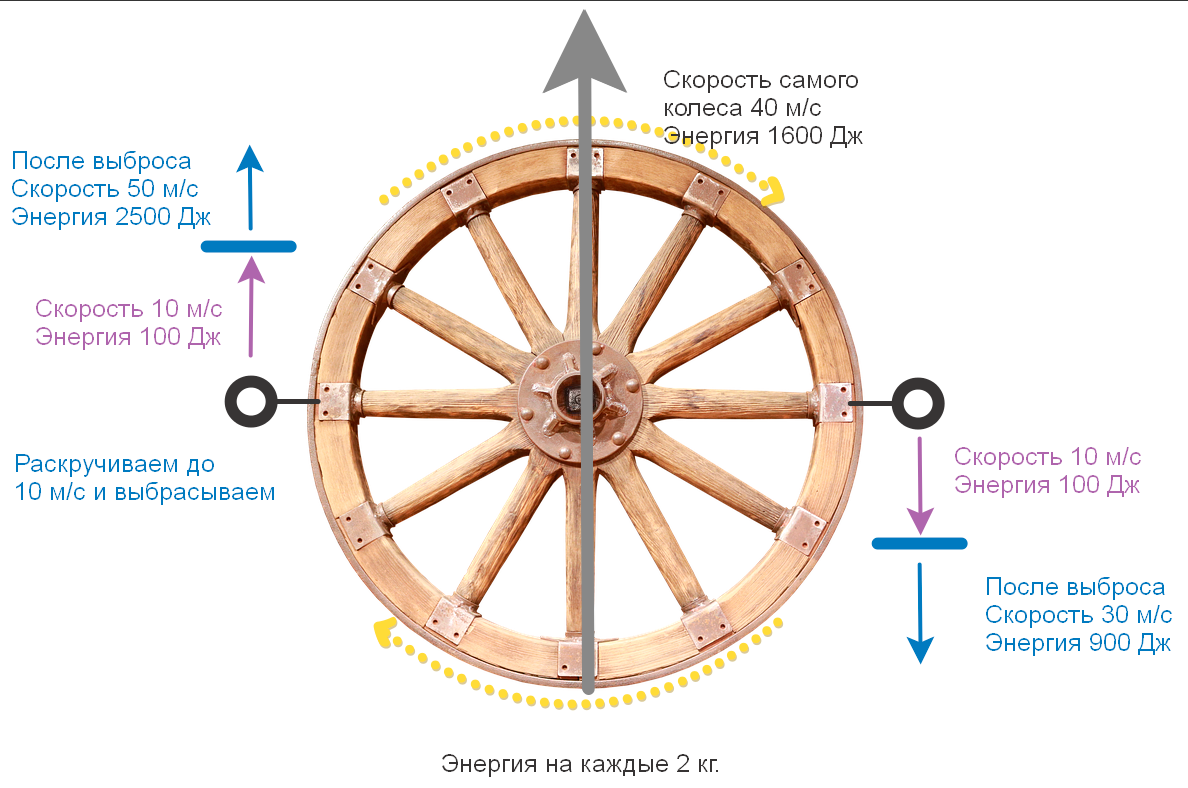
Here we again spent 200 J, and the accelerated one increased its energy from 1600 to 2500 = he received 900 J = and he again took all the energy spent on unwinding 200 J and +700 J, which the load that flew back lost (1600-900 = 700) ... Sometimes they say that the efficiency of a rocket engine becomes more than 100%, but you need to understand that 2 conservation laws work here at once (the law of conservation of energy and the law of conservation of momentum). We will consider them in the framework of classical physics - in which momentum is a property of space (if we throw a stone in a vacuum and without gravity at a speed of 10 m / s - then it will never stop and will always fly at a speed of 10 m / s - therefore that space is - even, symmetrical and without friction) - the momentum is described by three Newton's laws.



And energy is…. hell knows what, but it is described by three laws of thermodynamics, you can't figure it out without entropy and Schrödinger's cat - fortunately in orbital mechanics we can do without understanding where the energy comes from - we will consider it as a property of matter - “gasoline burns because it gasoline ", and any rocket engine has the following parameter: Specific impulse.







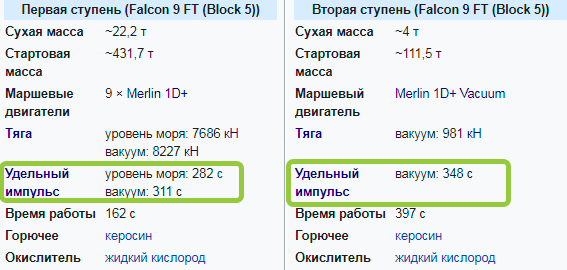
We multiply this number by 10 and we get the speed of fuel escape from the nozzle - for the second stage of Falcon 9 it is 348 * 10 = 3 480 m / s, from this parameter we can understand everything we need. And we will be content with Laplace's relativity - no matter at what speed we throw out the mass - in the example with a wheel and 2 bodies, weights always fly out at the same speed + -10 m / s relative to the wheel itself, and in the context of a rocket it is means that if 1 kg of fuel can accelerate the rocket from 0 to 10 m / s, then the same kilogram of fuel can accelerate the rocket from 10,000 to 10,010 m / s, despite the fact that in the second case, the rocket will receive a thousand times more energy - this is called the Aubert effect.



Now let's go back to the very first garage rocket example. There, at speed - the efficiency of the "engine" of the ball was higher, but first of all, the matter was in gravity - in order to raise the ball to a height, you need to spend energy, and when it falls, it returns, and if we measured the speed of the ball hitting the floor, then in the first the ball fell from a greater height and hit harder, and in the second from a lower height and hit weaker - he gave more energy, because he had more energy initially - he received it from the experimenter who raised it to a height and on Earth from the Oberth effect to get "Profit" is unrealistic.



But with Jupiter, the situation is different. I wrote in detail about gravity and cosmic velocities in the last article, here it will be very short. The fact is that gravity does not give / take away speed (km / s), but energy (Joules). And in the case of Jupiter, we began to "fall" on it at about zero speed and at the closest approach we accelerated to 50 km / s (we received 2,500 MJ of energy from it for every 2 kg), we turned on the engines and accelerated to 55 km / s and our energy became 55 * 55 = 3025 MJ, and when we flew "beyond the border" of its gravity - he took back not the speed (50 km / s), but the energy that he gave us (2500 MJ). there are 3025-2500 = 525 MJ left, to get the speed from the energy we extract the square root = 22.9 km / s. Here we got exactly the "profit", because we did not take off from Jupiter and we never had a speed of 50 km / s.It is very convenient to think of gravity as a pit.







And in the case of Jupiter, we sort of "pulled" the fuel from a depth of 10 thousand kilometers (from the Earth), and dropped it at the "depth" of 200 thousand kilometers and we flew out of the pit, and most of the fuel remained in the depth of this pit. (in the orbit of Jupiter), although we could just as well have come closer to the Sun and the effect would have been even greater - the closer to the massive body - the greater the "depth". Therefore, during interplanetary flights, the Obert effect can really give "profit" and it is always used, but before departure from the Earth - all additional energy is taken from the combustion of previous tons of fuel.

Tsiolkovsky's formula

Since the fuel always leaves at the same speed = the rocket gets the same acceleration, the “speed” margin of the rocket can be measured in km / s (characteristic speed), for example, the characteristic speed of 10 km / s means that the rocket can accelerate from 0 to 10 km / s, or first accelerate by 6, then decelerate by 1, and again accelerate by 3 (in total 10). And the mass of the fuel directly depends on the speed at which the fuel is ejected from the nozzle (specific impulse), and then Tsiolkovsky's curse arises.

$$

$$V=I*ln(\frac{m_1}{{m_2}})$$

V-Final velocity of the rocket

I-Specific impulse

M1- Initial mass of the rocket with fuel

M2- Final mass of the rocket without fuel



If we take a rocket with a mass of 271 kg entirely consisting of fuel and with a specific impulse of 3 km / s, then with acceleration from 0 to 3 km / s, the fuel mass will decrease by 2.71 times (number e) and we will have 271 / 2.71 = 100 kg of fuel, with an acceleration of 3 km / s, up to 6 km / s, the same thing will happen again and here there will be again 2.71 times less fuel 100 / 2.71 = 37 kg, and so on. Since the rocket design does not weigh 0 (usually the weight of the structure is taken at 10%), then we can safely take modifier 3. I will leave an example under the spoiler.





Although we simplified a lot, but the number turned out to be very close to reality (ideally, you need just ~ 18 km / s), and the Saturn 5 rocket that carried talking monkeys to the Moon had a launch mass of 3,000 tons, and only 5 tons returned from the Moon = 600 times less. And this rocket was the size of a 30-storey building (110 m). In fact, it is almost impossible to accelerate more than 6 times faster than the specific impulse. Although for 50 years they have been promising a nuclear engine with a specific impulse of 8,000 m / s, and with such an engine, a flight to the Moon and back would require only 8 kg. fuel, but so far this engine remains on the other side of the TV. Although in reality still worse, high-RI thrusters accelerate for a very long time and often cannot even overcome the acceleration of gravity on Earth, and they are not suitable for starting from the surface.and the most horrors just happen at the start.



To rise to the height of the moon, a launch speed of ~ 11 km / s is needed, and the main disadvantage of rockets is that they do not accelerate instantly. And although the Oberth effect does not give profit on Earth, it can be completely lost, because in addition to the specific impulse, the rocket has such an important parameter for launch: Thrust.







We divide kilo Newtons into tons 7680/549 = ~ 14 m / s, and we get the acceleration of the rocket per second, and on the surface of the Earth the acceleration of gravity is ~ 10 m / $$$^2$ , and if the engine worked for 10 seconds in vacuum, we would accelerate by 140 m / s (excluding the decrease in the mass of the rocket), but due to gravity, we accelerated by only 40 m / s, and the efficiency of the engine depends on the current speed , and as in the case of a garage rocket, when it received more energy from the ball at a lower altitude, the opposite process takes place for a rocket taking off, and the faster the rocket climbs, the faster the kinetic energy turns into potential energy and the less energy it gives fuel, or rather the efficiency the engine is still growing, but not as fast as it could if we were accelerating with a minimum climb. Therefore, the more the rocket is tilted towards the horizon, the slower the altitude grows and we get more from the Aubert effect. But then we rub against the atmosphere longer. Although the atmosphere creates many times less losses,compared to the benefit we are missing - friction creates temperature and we need a heavier thermal shield that will eventually have to be pulled into orbit. But that's not all, after ~ 2 minutes ~ 75% of the fuel burns out and the mass decreases by almost 4 times, but we have the same engine and, as it burned ~ 2.5 tons per second, it burns, only at first he was pushing ~ 600 tons with an acceleration of 14 m / s, and now he is pushing 150 tons with an acceleration of 14 * 4 = 56 m / s = G-forces are increased by 4 times. Of course, we can reduce the fuel supply, but then gravitational losses will increase (these are the last seconds before the separation of the first stage). Ultimately, all this leads to the fact that we lose about half of the fuel for these so-called gravitational losses (although this is more likely a lost profit).But that's not all, after ~ 2 minutes ~ 75% of the fuel burns out and the mass decreases by almost 4 times, but we have the same engine and, as it burned ~ 2.5 tons per second, it burns, only at first he was pushing ~ 600 tons with an acceleration of 14 m / s, and now he is pushing 150 tons with an acceleration of 14 * 4 = 56 m / s = G-forces are increased by 4 times. Of course, we can reduce the fuel supply, but then gravitational losses will increase (these are the last seconds before the separation of the first stage). In the end, all this leads to the fact that we lose about half of the fuel for these so-called gravitational losses (although this is rather a lost profit).But that's not all, after ~ 2 minutes ~ 75% of the fuel burns out and the mass decreases by almost 4 times, but we have the same engine and, as it burned ~ 2.5 tons per second, it burns, only at first he was pushing ~ 600 tons with an acceleration of 14 m / s, and now he is pushing 150 tons with an acceleration of 14 * 4 = 56 m / s = the G-forces are increased by 4 times. Of course, we can reduce the fuel supply, but then gravitational losses will increase (these are the last seconds before the separation of the first stage). Ultimately, all this leads to the fact that we lose about half of the fuel for these so-called gravitational losses (although this is more likely a lost profit).only in the beginning he was pushing ~ 600 tons with an acceleration of 14 m / s, and now he is pushing 150 tons with an acceleration of 14 * 4 = 56 m / s = the G-forces are increased by 4 times. Of course, we can reduce the fuel supply, but then gravitational losses will increase (these are the last seconds before the separation of the first stage). Ultimately, all this leads to the fact that we lose about half of the fuel for these so-called gravitational losses (although this is more likely a lost profit).only in the beginning he was pushing ~ 600 tons with an acceleration of 14 m / s, and now he is pushing 150 tons with an acceleration of 14 * 4 = 56 m / s = the G-forces are increased by 4 times. Of course, we can reduce the fuel supply, but then gravitational losses will increase (these are the last seconds before the separation of the first stage). Ultimately, all this leads to the fact that we lose about half of the fuel for these so-called gravitational losses (although this is more likely a lost profit).that we are losing about half of the fuel for these so-called gravitational losses (although this is rather a lost profit).that we are losing about half of the fuel for these so-called gravitational losses (although this is rather a lost profit).



Since the fuel must be thrown away (burned) at a minimum altitude with a minimum upward acceleration, the rockets are first accelerated to the first cosmic velocity (~ 7.9 km / s for the Earth) and put into the lowest circular orbit (LEO 180-200 km) and absolutely not it is important where you fly to the Moon / Mars or the GSO, you first need to go to circular motion and stop "arguing" with gravity.



Fuh, having gone through all these overloads, gravitational losses, a fiery atmosphere and other near-earth horrors - we find ourselves in a low reference orbit (LEO ~ 180 km). Let's say we need to go to a geostationary orbit (at an altitude of ~ 35,000 km). You have probably seen the most moronic trajectory of the transition between orbits many times in Hollywood blockbusters - when the rocket is turned vertically and the engines are turned on against gravity. In the lowest orbit, there is only 200 km to the earth - 3 times less than from Moscow to St. Petersburg !!! .. The acceleration of free fall at this altitude is only 5% less, and amounts to ~ 9.2 m / s per second. We are constantly falling down, but because of the forward speed of 7.9 km / s, the round earth is constantly “slipping away from under our feet,” so although we are constantly falling, our height does not change. And fortunatelybeing in a circular orbit, we can only accelerate forward and gravity will not interfere with us ...



But there is another option, less moronic in comparison with accelerating up, but no less moronic in general. Let's look at it too, so, clean neighing.



We are moving forward, accelerating upward, gravity will interfere with us, but we have 3 dimensions !!! We can accelerate sideways. What will happen?

For convenience, let's take a rocket speed of 8 km / s and a propellant take-off speed of 8 km / s, and see what speed the fuel will have after takeoff.







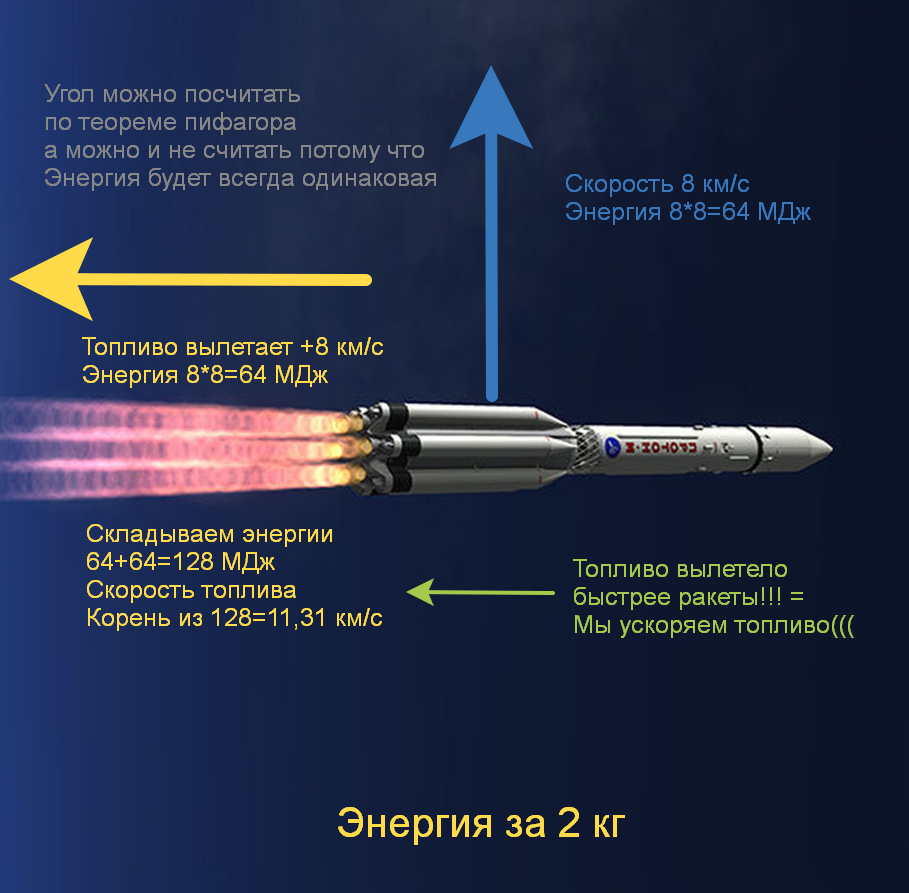
So initially the fuel moved 8 km / s (64 MJ) forward along with the rocket, then + 8 km / s (+64 MJ) flew out to the left relative to the rocket, and we can calculate the angle (45 degrees) and say that the fuel moves 11.31 km / s relative to the picture and its energy is 128 MJ, or we may not consider the angle and say that the fuel moves 8 km / s to the left (64 MJ) and at the same time 8 km / s upward (64 MJ), but its energy is still 128 MJ. that is, the fuel accelerated anyway, but we were going to accelerate the rocket ... God, what happened to the rocket !? Has it slowed down and is about to fall to Earth?



Don't worry, everything is fine with the rocket - it also accelerated, and it accelerated by the same 64 MJ, in order to calculate the angle and speed, you need to know the difference in masses, but something else is important for us. In fact, we got the same thing as in the first example with the wheel, when it did not move and we had 2 weights accelerated in opposite directions, having received the same energy, and the efficiency was then 50% - a surprise - the Obert effect depends not only on speed, but also from the direction and stops working at any deviation from the current velocity vector. In this example, we received 3 times less energy than if we threw fuel back, and this is with a nuclear impulse of 8 km / s (at 3 km / s ~ 6 times less) - this is called losses on maneuvers, and in fact, after entering orbit, it is almost impossible to turn left / right and therefore the rockets are accelerated only forward,and if, when entering orbit, you miss at least 30 degrees, then it is cheaper to launch a new rocket than to change the velocity vector of this one. Fortunately, in the era of GPS and computers, rockets enter orbit with very high accuracy, and maneuver losses are near zero.

How to climb from a height of 200 km to an altitude of 35,000 km?

Considering all of the above, the only direction of acceleration of the rocket is forward and perpendicular to gravity.







When accelerating perpendicular to gravity - the height increases from the opposite side of the planet (gravitating body) and to fly from the Low reference orbit (~ 200 km + speed ~ 8 km / s) to the Geostationary orbit (~ 35,000 km + speed ~ 3 km / s ), we need to accelerate to ~ 10.4 km / s (8 + 2.4), our circular orbit will become elliptical and on the opposite side we will rise to an altitude of 35,000 km, and our speed will be 1.7 km / s (at distance gravity takes energy). At this point, we will again move perpendicular to gravity and we need to accelerate to ~ 3 km / s in order to increase the altitude from the opposite side again and make our orbit perfectly round - This is called the Homan flight and this is the cheapest way to travel in space - we always we accelerate only forward and gravity never bothers us.



Flights between the planets are also made along the same trajectory, and as you may have already guessed, although the minimum distance from Earth to Mars is ~ 55 million kilometers, this almost does not affect anything, because we will arrive on Mars from the opposite side of the Sun after passing about 400 million. km - that's why the flight lasts about 8 months.

It is extremely difficult to reduce the flight time, or rather to quickly fly off the Earth, it is easy and at a starting speed of ~ 16.5 km / s we will reach Mars in 3 months, but when approaching it, we will not have the same velocity vectors. To put it simply, we will move 1 km / s and Mars 1 km / s, but at the same time we will fly forward, and Mars to the left and we will need a giant braking impulse. To be more precise, the difference in speeds will be 21 km / s, + we also need 16.5 km / s for a start from the Earth = 37.5 km / s = the mass of the rocket yourself.

?

If your grandfather was a well-to-do Reptilian and left you a legacy of a couple of tons of antimatter, then of course you can fly to Mars along any trajectory at any speed (even every weekend). But practice shows that mostly poor Reptilians who do not even have money for their own flying saucer fly to Earth - have you seen at least one UFO parking lot? - that's it - because the Reptilians arrive by taxi.



Therefore, all that remains for us is a low-cost Homanovsky flight. But don't be in a hurry to despair - orbital mechanics is very paradoxical. Why do you think, after the flight of humans to the moon, 4 Mars rovers were sent to Mars in 50 years, and only 1 (and then Chinese) was sent to the Moon rover?





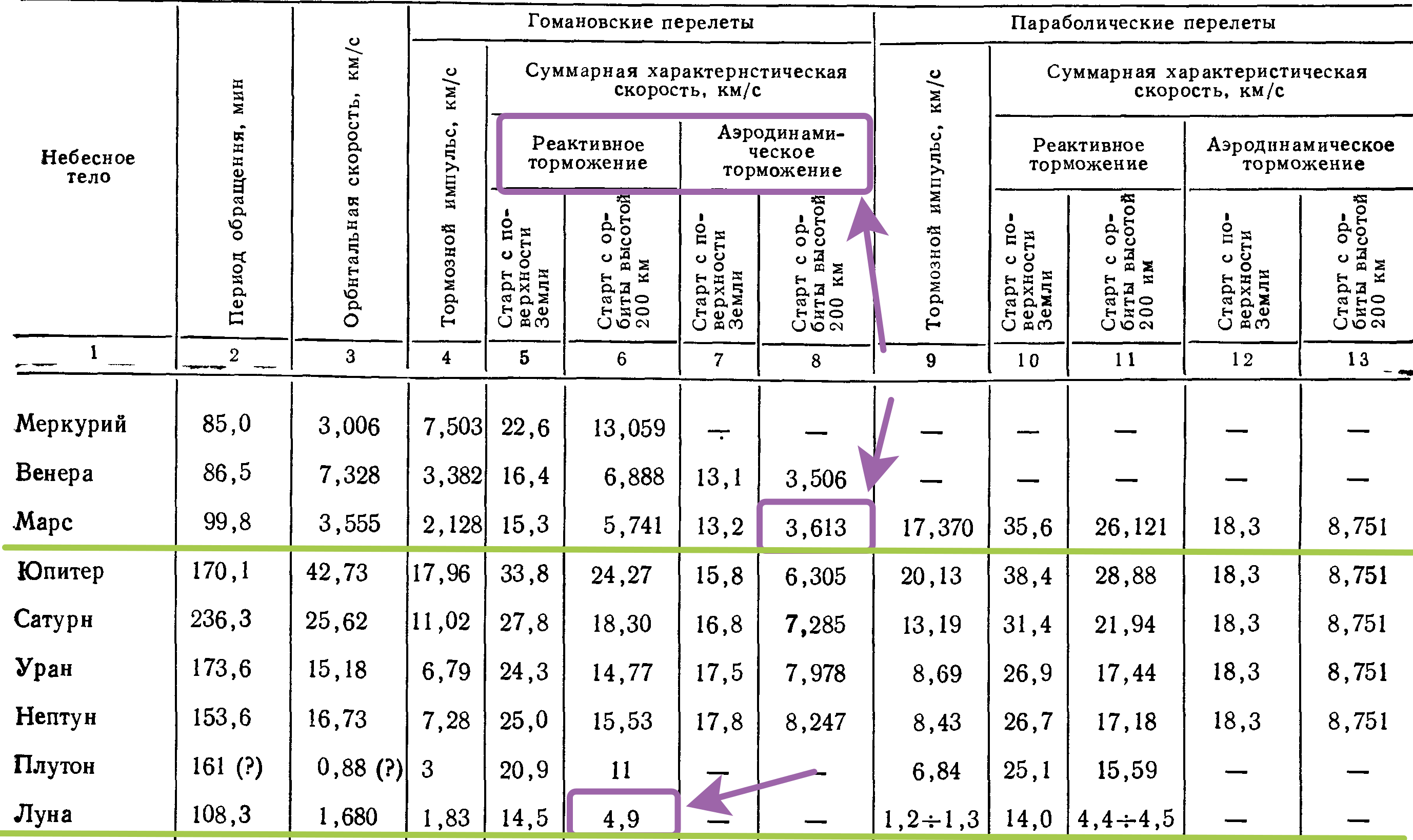
Table: V.I. Levantovsky The mechanics of space flight in an elementary presentation.

Note: Calculations by Levantovsky taking into account losses.



And all because in order to reach the Moon you need a starting speed of 11.1 km / s (I do not take into account losses - this is an ideal flow rate), and to go to Mars you need a starting speed of 11.5 km / s, only 0.4 km / s more, but at the same time, engines will have to slow down on the Moon (1.83 km / s for entering the Moon's orbit and + 1.68 km / s for landing on the lunar surface = 3.51 km / s), and on Mars can use the atmosphere for braking. And in fact it is cheaper to launch a satellite into the Martian orbit than into the Lunar orbit !!! I'll tell you even more, in order to launch a satellite to the GSO we need an impulse of 10.4 km / s + then another 1.3 = 11.7 km / s, and to Mars 11.5 km / s (although you need to take into account that thermal protection is not weighs 0).

Of course, this does not apply to Humans, because in 260 days of flight to Mars - Humans will eat more than a rocket, but from the point of view of cargo, it is extremely surprising - to send a tractor to Mars orbit, cheaper than to the Moon's orbit.



It is unlikely that it will be possible to completely land the tractor on the surface of Mars (the atmosphere is too "empty"), but nevertheless, the lion's share of the speed can also be extinguished with its help, and landing cargo on Mars is also cheaper than on the Moon (or at least comparable). The atmosphere offers amazing possibilities.



Returning from Mars is, of course, much more expensive than from the Moon. Although if you dream a little and imagine that we can completely brake about the atmosphere, then we need 11.5 km / s there and 5.7 km / s back = 17.2 km / s, and for the Moon 11.1 there + 3, 51 * 2 (landing / takeoff) = 18.12 km / s - ~ 0.9 km / s more))). But the gravitational losses at the start from Mars will be more than from the Moon, and thermal protection is needed, so in reality it will turn out 3-5 times more expensive (in terms of fuel mass) for cargo, and for monkeys it is even scary to imagine.



Again, this is if we are hauling fuel to return from Earth. If we produce fuel at the landing site, then the situation changes dramatically and for departure from the Moon to Earth we need 3.51 km / s (from Mars 5.7) - Lunar fuel is cheaper than Martian fuel, but landing on Mars is cheaper and it is easier for us to build production itself, and the curse of Tsiolkovsky is a very terrible thing, and even saving 1 km / s on landing, we can send 1.5 times more payload.



Surprisingly, colonizing Mars even has advantages over the Moon. And the Moon itself is easier to colonize from Mars than from Earth. Earth-Moon 11.1 km / s, and Mars-Moon 5.7 km / s. And if there was life on Mars too, they would have colonized our Moon long ago.



Orbital mechanics is paradoxical - gravity creates a "relief" and the solar system is actually not the same as can be seen in a telescope. In the next article we will consider this "relief" in more detail and will try to find the answer to the question - where is the cheapest fuel in the solar system. And to understand this "relief" we only need the Tsiolkovsky formula and the Second space velocity (be sure to read the last article about space velocities). And all with the simplest examples.



Those who have read the last article know that I have a familiar Reptiloid, and after the fifth New Year's glass he told me this! He says they have the technology they use to change the orbits of entire planets. First they take "Jupiter" and some small "Pluto", lower their orbits closer to the "Sun", but "Pluto" turns in the opposite direction and collides head-on with the "Jupiter" at a speed of 600 km / s each, and although Jupiter is 20,000 times heavier than Pluto, but because of the tremendous collision speed, it heats up to several thousand degrees and begins to shine like a light bulb. And then they throw this "light bulb" from their star system to another at a speed of 200-300 km / s. Yes, the flight takes a long time - several thousand years, but they move with comfort - with a mini "Sun" (it cools down for a very long time).Then they fly to the desired star, deploy their group of flying saucers and throw all the planets back to their home star. And they have already collected several thousand planets - they already have nowhere to park them. They have even blinded 80 "Jupiters" into 1 and lit the second "Sun".



He has not yet told me how these saucers fly, but he has already told a lot of other things, so be sure to subscribe to the channel - there will be UFO technologies further.



Well, be sure to repost, or do you really like what is happening with the Internet? When you go into YouTube trends - and there, in the top of the video, Vlad is bathed in paper ... chips. Don't you understand why this is happening? - and all because schoolchildren make reposts - and you don't !!! As Confucius said in his letter to Aristotle: - Whoever does not want to repost himself - will read what schoolchildren repost!







What do you want like in American YouTube? - reposting is the sacred duty of every Internet user! Therefore, do not let Vlad paper degrade the Internet !!! For your sake and future generations - repost!



The last article about cosmic speeds and gravity .



Sometimes, between states, I'm neither alive nor dead - I collapse on twitch .