Practical Application of Algorithm for Zeckendorff Representation

Like in the past

I wrote an article on Recursive Zeckendorff Algorithm: post

Sample code

def le_fib(limit, fib)
  theoretical = fib[fib.count - 1] + fib[fib.count - 2]
  return fib.last if theoretical > limit

  fib << theoretical
  le_fib(limit, fib)
end

def main(target,result)
  temporary = le_fib(target, [1,1])
  result << temporary
  return result if target - temporary <= 0

  main(target - temporary, result)
end
pp main(gets.to_i,[])

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

Le_fib  function  - recursively searches for a Fibonacci series with a limit, so that the next number is not greater than the input target number  . It is important here that we are not interested in the entire Fibonacci series, only its end is important to us.

The  main  function - recursively searches for an array whose numbers are Fibonacci numbers, and which would give us an input number in total.

Although in truth, the comments suggested a more elegant solution:

One cycle and business

n, F = 100, [1, 2]
while F[-1] < n do
  F << F[-2] + F[-1]
end
F.reverse.each do |f|
  if f <= n
    n -= f
    print f
    print '+' if n > 0
  end
end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

In practice, I will use the second algorithm as it is less overloaded with unnecessary actions.

Problem statement where we will "push this algorithm"

There is a certain set of products, relatively speaking:

[Chicken, tomatoes, lavash, mushrooms].

These products have both cost and end-user value.

For example, the gradation can be done as follows

[chicken> tomatoes> mushrooms> lavash] .

, 1 "Low cost", 1 "High cost" .

().

( Ruby) , .

, .

x y .

1. 

   

2. Y - .
   
   
   
   - , .
   
   
   
   . Y

   
   
   
   
   

   

3. 1 89. , "Middle cost" .
   
   
   
   3 x = 1 y = 143.

   
   
   
   
   

, :

• - ( )

  
  
  
  
  

• Collector, Hash ( -> , -> )

  
  
  
  
  

, autoloader , .

, Telegram , .

, ,

@fib = [1,2,3,5,8,13,21,34,55,89]
    def collect_the_items
      food_hash = Hash.new
      (0..9).each do |iterator|
        food_hash[@fib[iterator]] = FOOD.first[iterator]
      end
      puts food_hash.map{|key,value| "#{key} - #{value}"}
    end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, :

def get_sequence(limit)  
  result = []  n, fib = limit, [1, 2]  
  while fib[-1] < n do
    fib << fib[-2] + fib[-1]  end
  fib.reverse.each do |f|    if f <= n
      n -= f
      result << f
    end
  end
  result
end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

- .

def generate_food
          food_array = Collector.collect_the_items
          food = []
          rarity = rand(1..143)
          get_sequence(rarity).each do |key|
            food << food_array[key]
          end
          food
end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, 6 , .

. - .

:

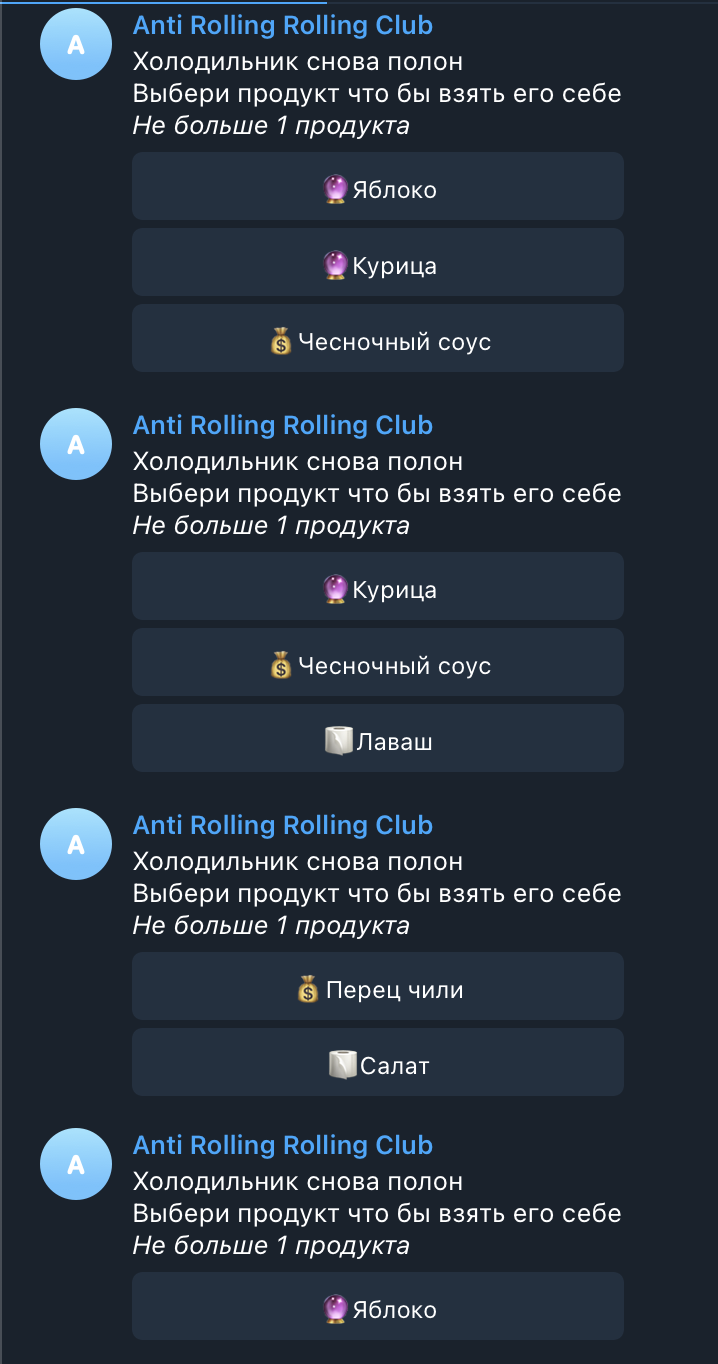
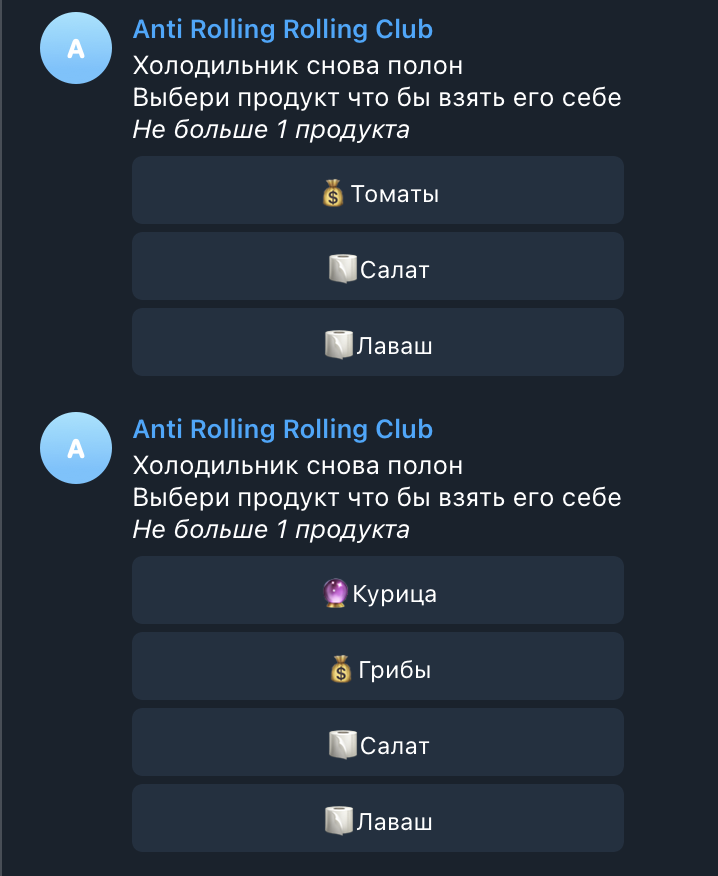
Low cost : ?

Mid cost : ?

High cost : ?

Applying the Zeckendorff representation algorithm completely satisfies me. That is, it performs the task assigned to it.

One of the first comments under the article on which this practical application is based, just asked me the question: "but really, where can this be applied?" As you can see, this algorithm can be used for such tasks.

And I'm not saying that this is the only correct option for compiling a list of products for my bot, but it really is quite capable and works.