Clever Geek Handbook

Visual representation of factoring a number using trigonometric functions

Let's take a hyperbola of the form:





f (x) = n / x

Here n is an odd number, the divisors of which must be found. Multiply f (x) by cos [π⋅f (x)] (note - the brackets () and [] are equivalent and do not add additional meanings). And take the module of the resulting function g (x):





| g (x) | = | f (x) ⋅cos [π⋅f (x)] |

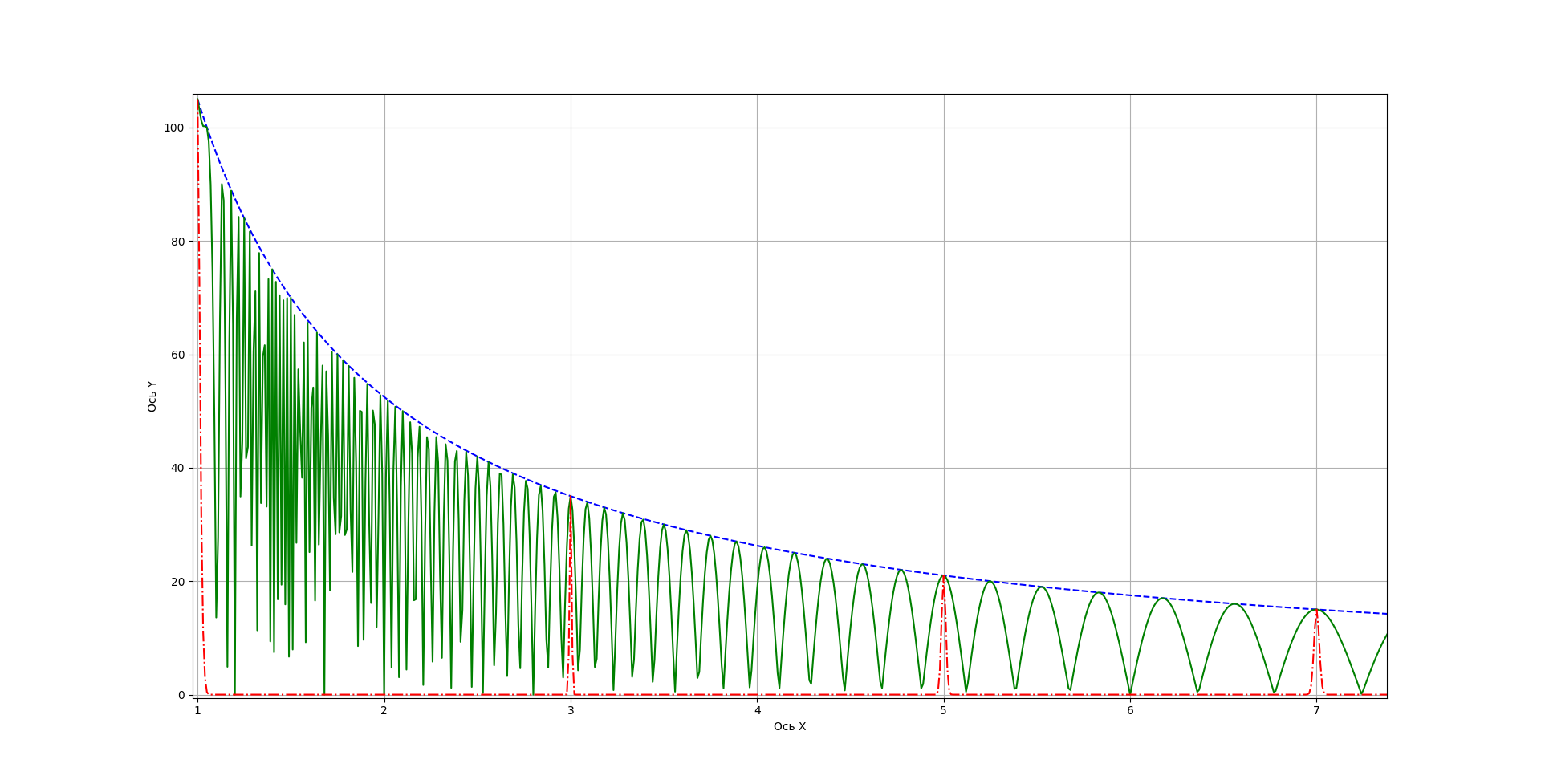
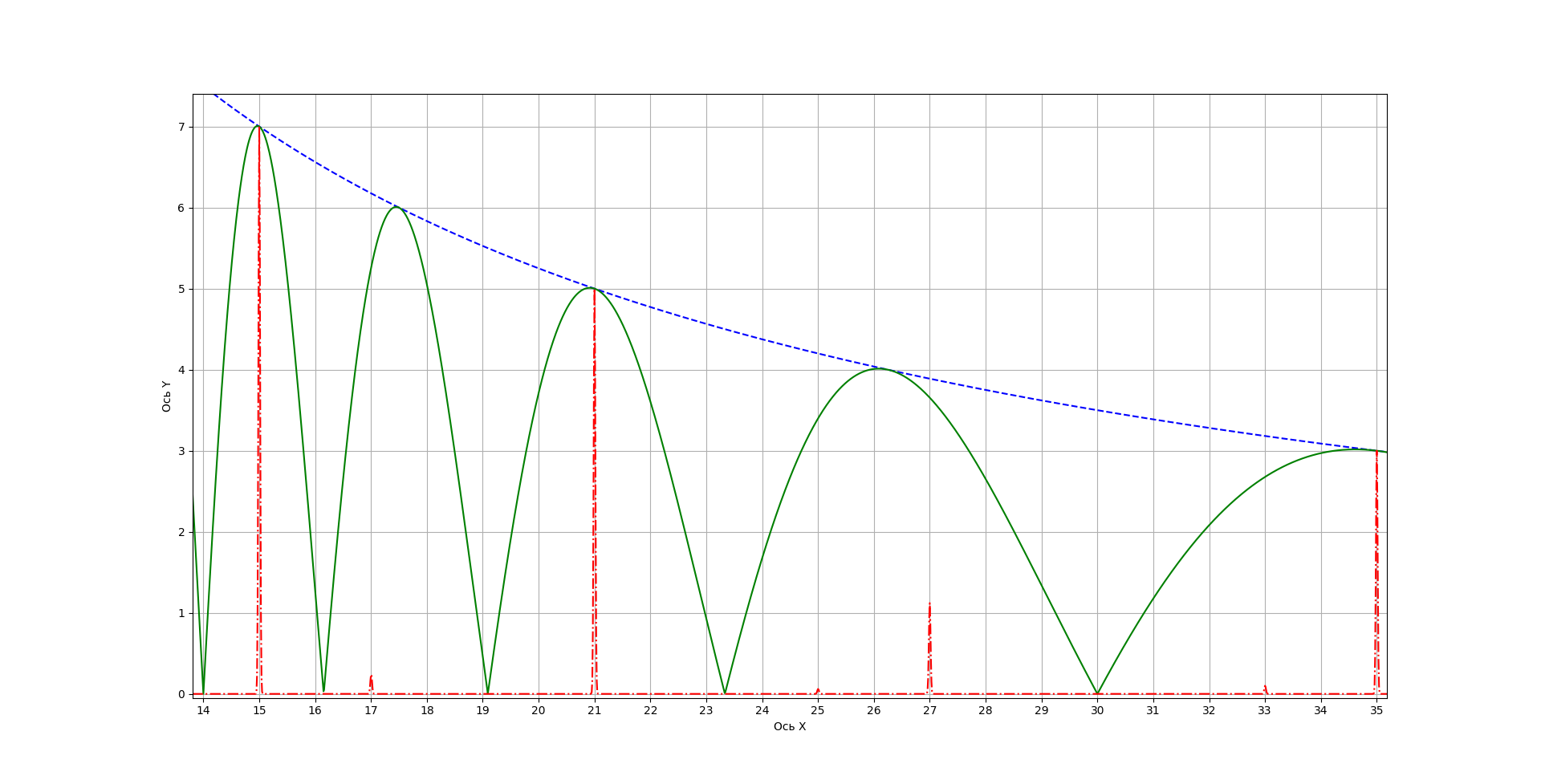
The graphs f (x) and | g (x) | are shown in Fig. 1. n is taken equal to 15. And this is one of the main drawbacks of the method, for large values ​​of n the argument of the cosine changes with a very high frequency.





Figure 1 - Graph of functions f (x) = 35 / x and | g (x) | = | f (x) ⋅cos [π⋅f (x)] |
1 - f(x)=35/x |g(x)|=|f(x)⋅cos[π⋅f(x)]|

, , 2 .





Figure 2 - Graph of the function f (x) ⋅cos [π⋅f (x)] ^ 10
2 - f(x)⋅cos[π⋅f(x)]^10

"" (. . 3) (.. g(x)) [sin(π⋅x/2)⋅sin(3π⋅x/2)⋅sin(5π⋅x/2)⋅sin(7π⋅x/2)]^20.





n. 1, 3, 5, 15.





Figure 3 - Filtering f (x) ⋅cos [π⋅f (x)] ^ 10 using sin (π⋅n⋅x / 2)
3 - f(x)⋅cos[π⋅f(x)]^10 sin(π⋅n⋅x/2)





n=105, 4, 5 1, 3, 5, 7, 15, 21, 35. 105 .





Figure 4 - Hyperbola f (x) = 105 / x and possible divisors
4 - f(x)=105/x
Figure 5 - Hyperbola f (x) = 105 / x and possible divisors (continued)
5 - f(x)=105/x ()

"" , .





.. , p-V-T , . . 6 10.





Figure 6 - Multipliers of numbers 21, 77, 187, 323, 437 in 3D.
6 - 21, 77, 187, 323, 437 3D.

(-cos[π⋅f(x)]) :





  1. 1 n Nn=(n-1)/2





  2. N x Nx=n⋅(x-1)/2⋅x





  3. The x coordinate of the Nth period is calculated by the formula x N = n / (n-2⋅N)





  4. The ratio of the coordinate value x N + 1 to x N : x N + 1 / x N = 1 + 2 / (n-2⋅N)





  5. If you imagine a number large enough n as the product of P (1 + 2 / (n-2⋅N)) from 1 to N n , the first ≈63.2% of the terms in the product will give the number e.











More articles:


All Articles