Continuation of yesterday's article on fYolka below.
Basic functions
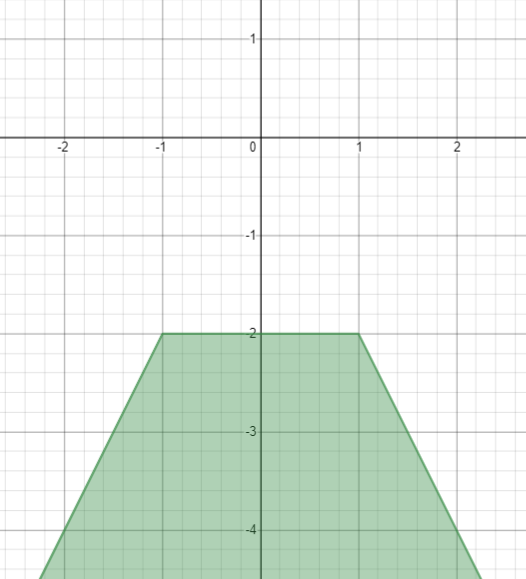
Trapezoid
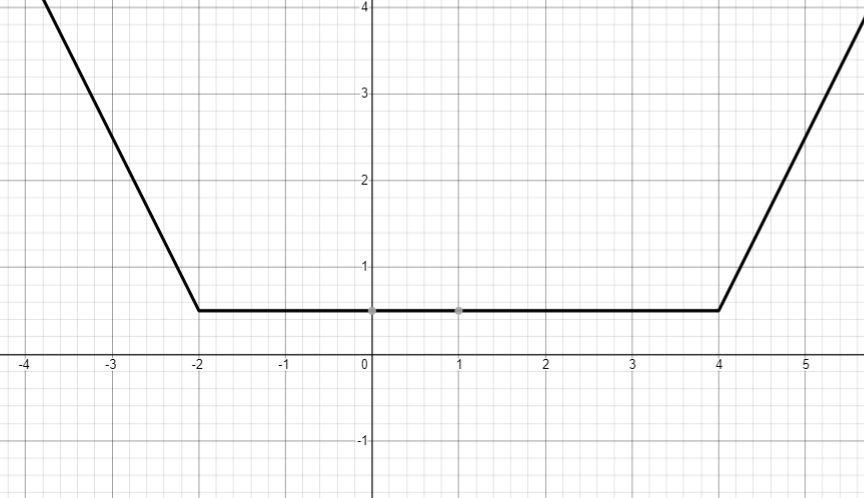
Here the modulus of the number is applied twice, changing the constants under the modulus and the subtracted value, we can adjust the length of the segment with a constant value of y and the value of y itself on this segment. This feature will come in handy later for drifts and buckets.
Alternative ellipse
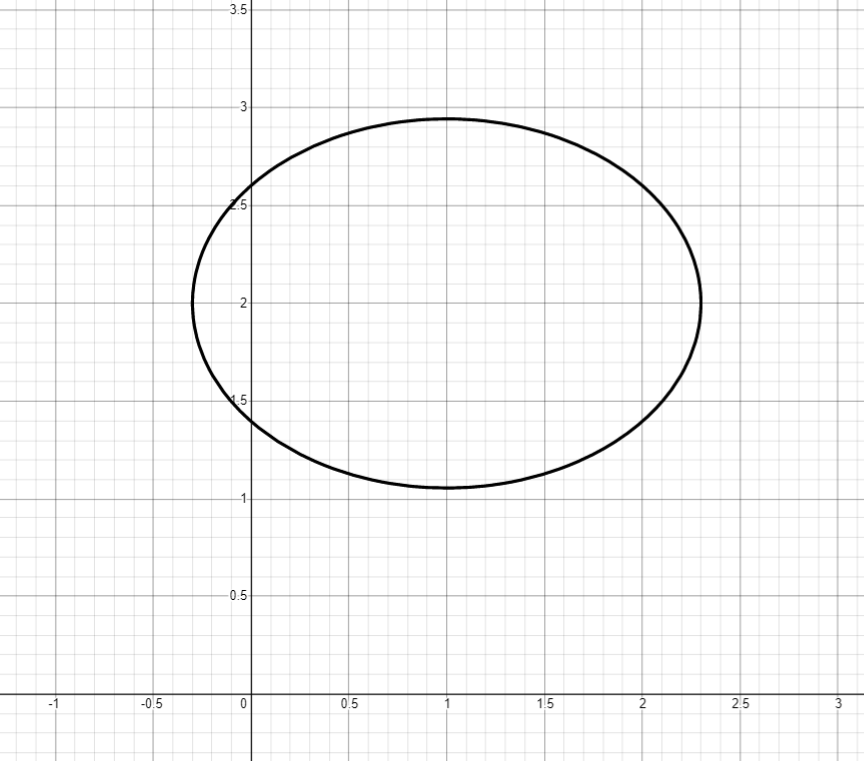
Alternative ellipse notation. The constants inside the brackets are responsible for the coordinates of the center of the ellipse, the constants in front of the brackets are for the compression ratio along the axes, the number behind the root is the radius.
Ellipse by two points

, - , (A B ) . .
, .
- :
-
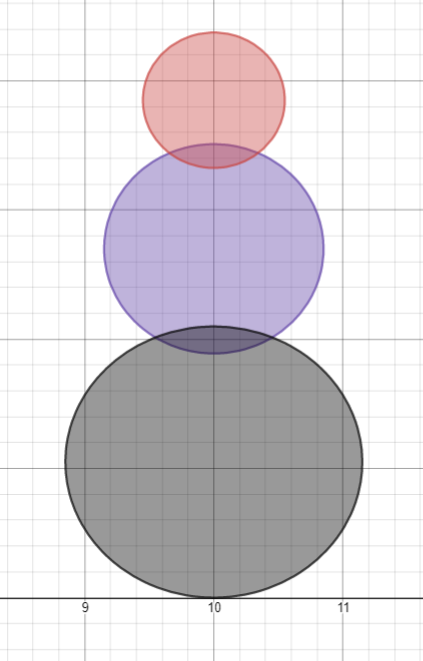
- min .

!
-
- ,

, - 2 , - .
-
, .
:

,

-

-


s4 , >0, <0, .
-
- x = 10, , , .
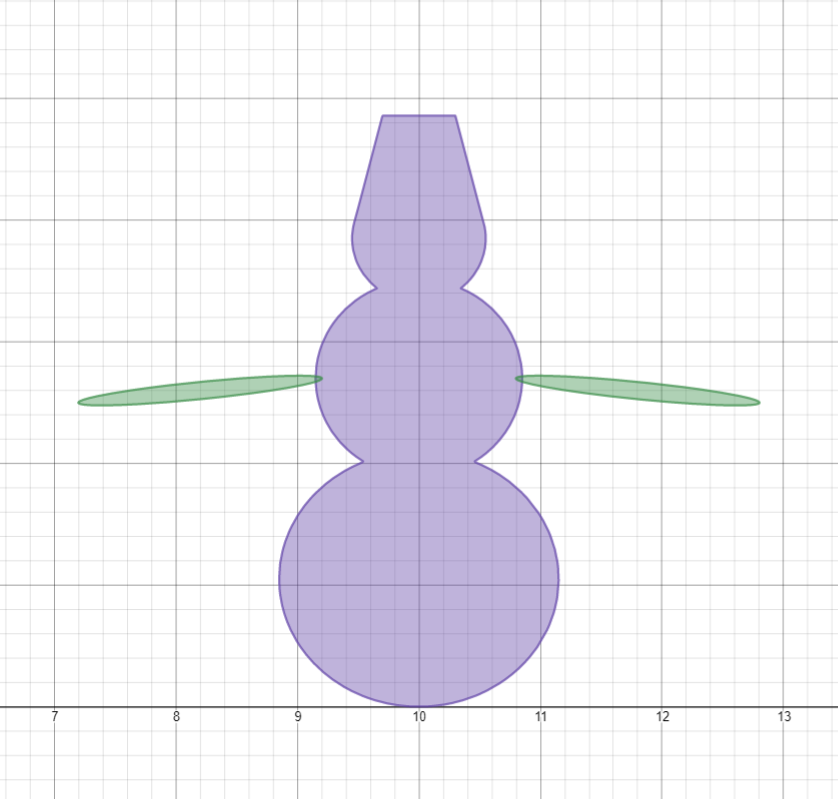
, = 10, = 2.55

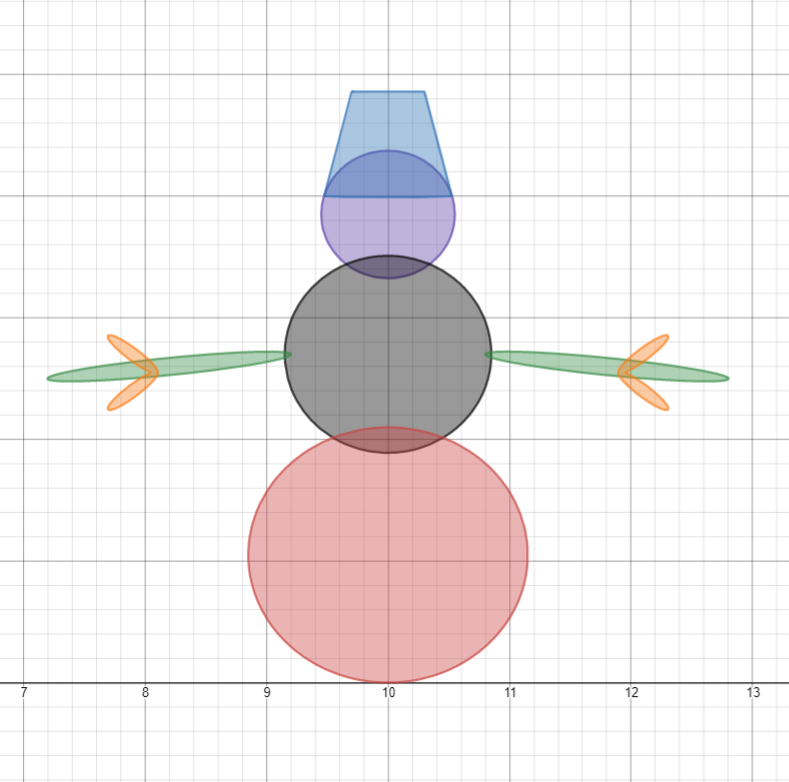

- 2

-

desmos
s_{1}=\sqrt{\left(x-10\right)^{2}+1.1\left(y-2.7\right)^{2}}-0.85
s_{2}=\sqrt{\left(x-10\right)^{2}+1.2\left(y-1.05\right)^{2}}-1.15
s_{3}=\sqrt{\left(x-10\right)^{2}+1.1\left(y-3.85\right)^{2}}-0.55
s_{4}=2-1.9\left|x-9.7\right|-1.9\left|x-10.3\right|-\left(\frac{\left(\left|y-4\right|+y-4\right)}{2}+\frac{100\left(\left|y-4\right|-y+4\right)}{2}\right)
h_{1}=\sqrt{\left(\left|x-10\right|\ -\ 0.8\right)^{2}+\left(y-2.7\right)^{2}}+\sqrt{\left(\left|x-10\right|\ -\ 2.8\right)^{2}+\left(y-2.5\right)^{2}}-2.015
h_{2}=\sqrt{\left(\left|x-10\right|\ -\ 1.9\right)^{2}+\left(y-2.55\right)^{2}}+\sqrt{\left(\left|x-10\right|\ -\ 2.3\right)^{2}+\left(\left|y-2.55\right|-0.3\right)^{2}}-0.51
\min\left(s_{1},\ s_{2},s_{3},-s_{4},h_{1},h_{2}\right)\le0
100\left(\left|x-10\right|-0.2\right)^{2}+100\left(y-3.95\right)^{2}\le1
\left(300\left(\left|x-10\right|-0.03-0.-\left(y-3.6\right)\right)^{2}+3000\left(y-3.6\right)^{2}\right)\le1
- . .

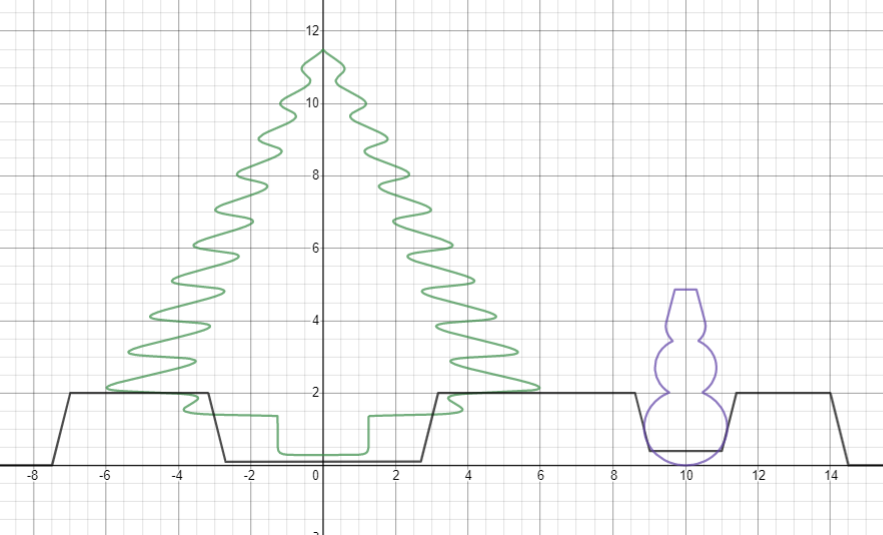
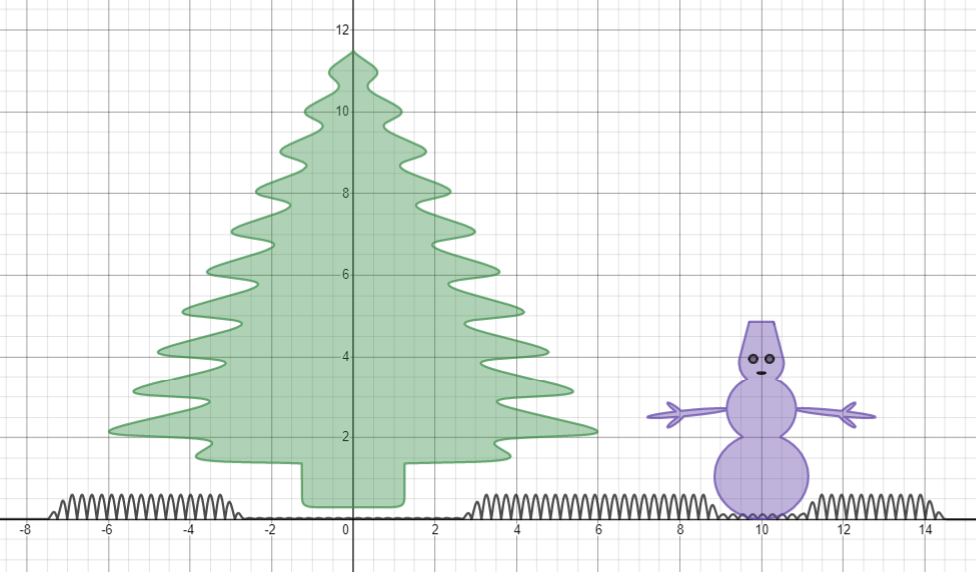
d_{1}=-\left|x+7\right|-\left|x-14\right|+22
d_{2}=\left|x+2.7\right|+\left|x-2.7\right|-6.35
d_{3}=\left|x-9\right|+\left|x-11\right|-2.8
d=d_{1}+\left|d_{1}\right|+d_{2}-\left|d_{2}\right|+d_{3}-\left|d_{3}\right|
0.3d\left|\sin\left(13x\right)\right|
. - " ", , , x .

mod,


, .
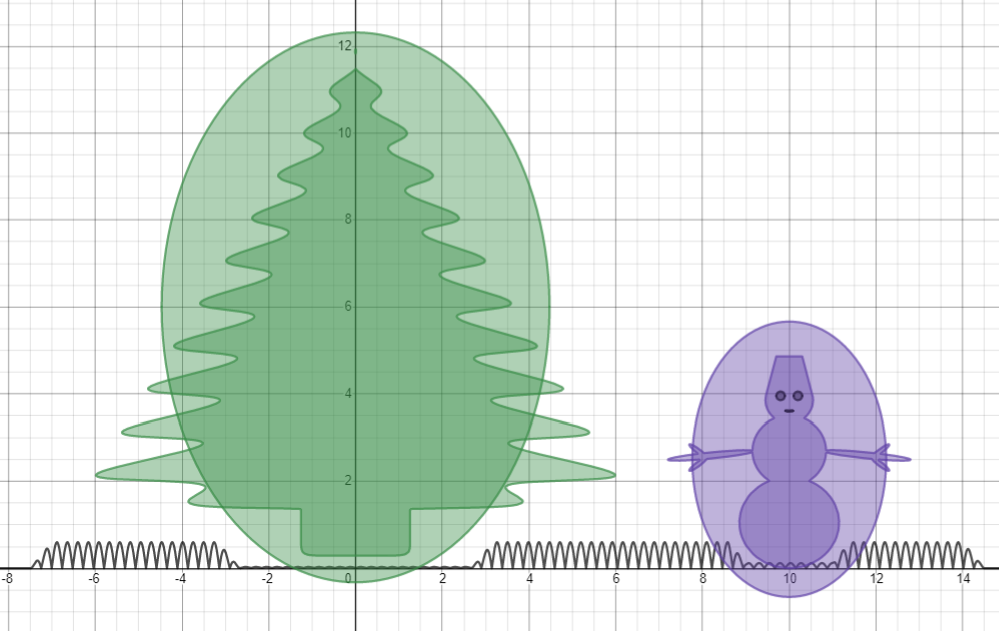

f_{1}=\sqrt{\left|\operatorname{mod}\left(x,2\right)-1\right|}+\sqrt{\left|\operatorname{mod}\left(y,2\right)-1\right|}-0.45
f_{2}=2xx+\left(y-6\right)^{2}-40
f_{3}=2\left(x-10\right)^{2}+\left(y-2.5\right)^{2}-10
\min\left(-f_{1},f_{2},f_{3}\right)\ge0
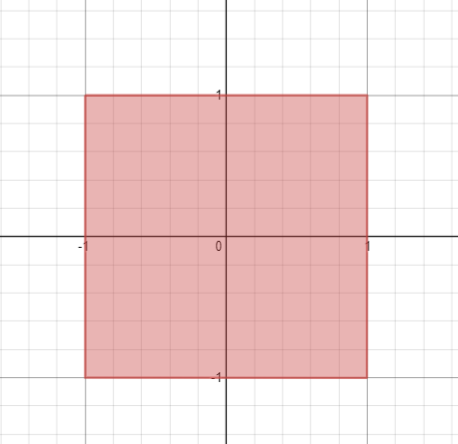
- . , |x| .
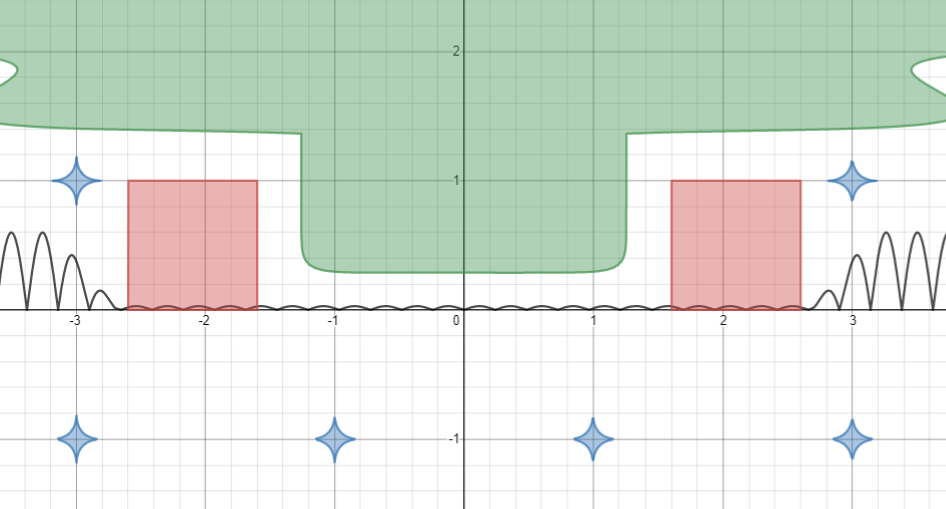
\max\left(\left|\left|x\right|-2.1\right|,\left|y-0.5\right|\right)\le0.5

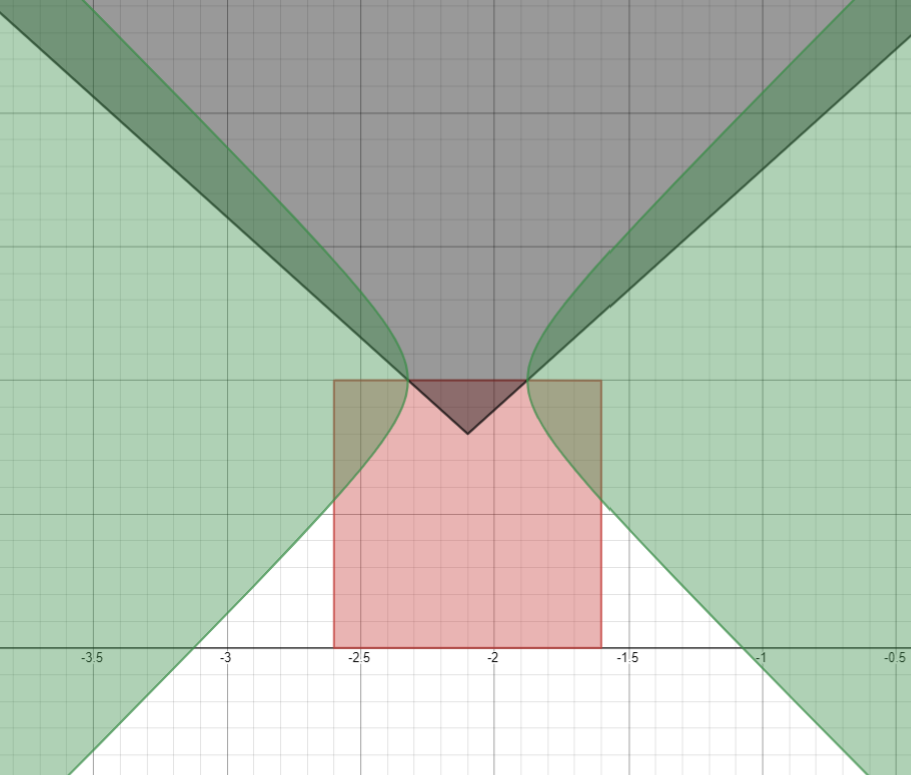

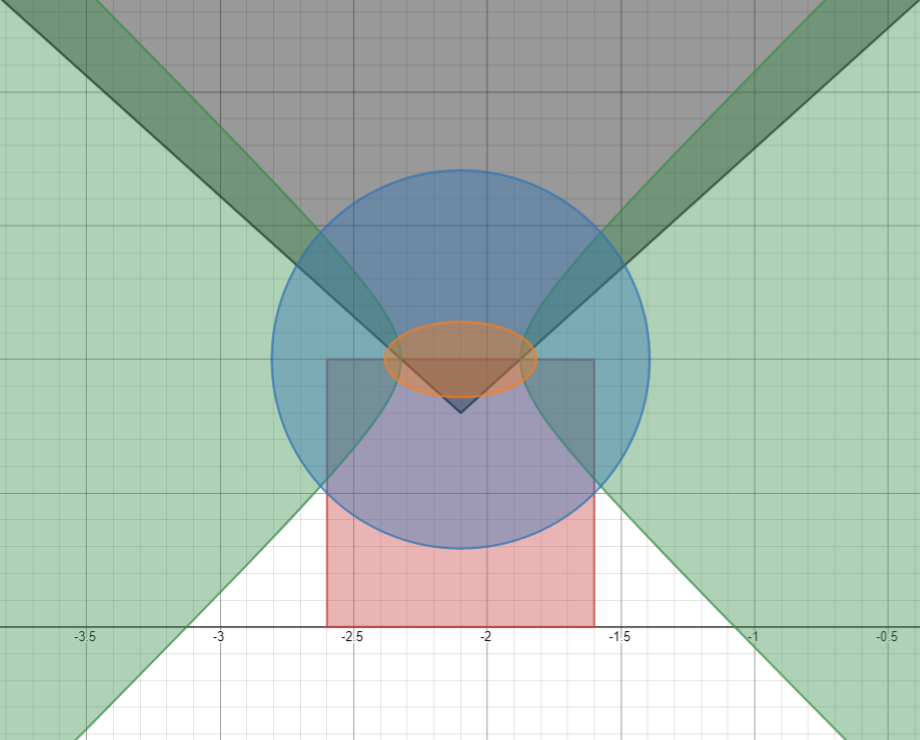
:
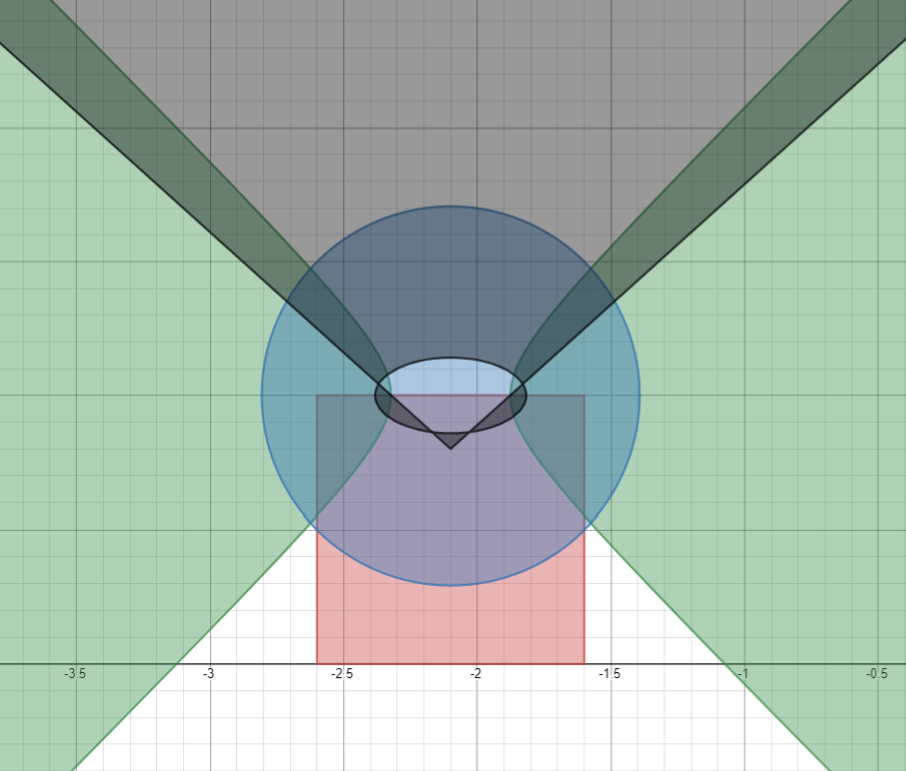
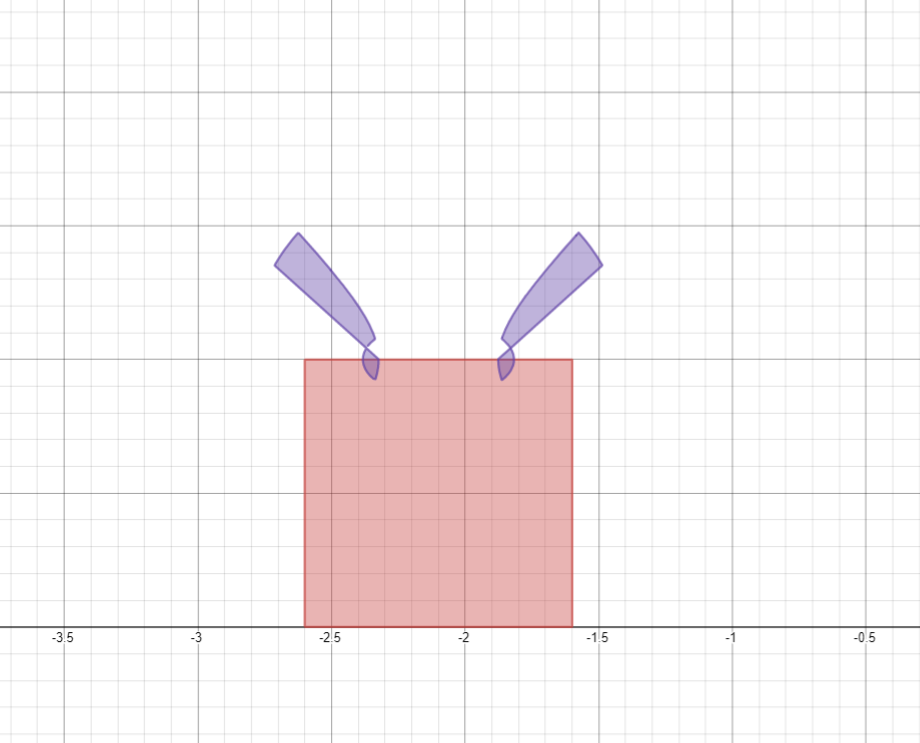
j_{1}=\left|0.9\left|\left|x\right|-2.1\right|\right|-\left(y-1\right)-0.2
j_{2}=\left|\left|x\right|-2.1\right|^{2}-\left(y-1\right)^{2}-0.05
j_{3}=0.2\left|\left|x\right|-2.1\right|^{2}+0.2\left(y-1\right)^{2}-0.1
j_{4}=\left(0.5\left|\left|x\right|-2.1\right|\right)^{2}+\left(y-1\right)^{2}-0.02
\max\left(j_{1}j_{4},\ -j_{2},\ j_{3}\right)\le0
, , .
2021 MMXXI,
""
t2,

"",

V-
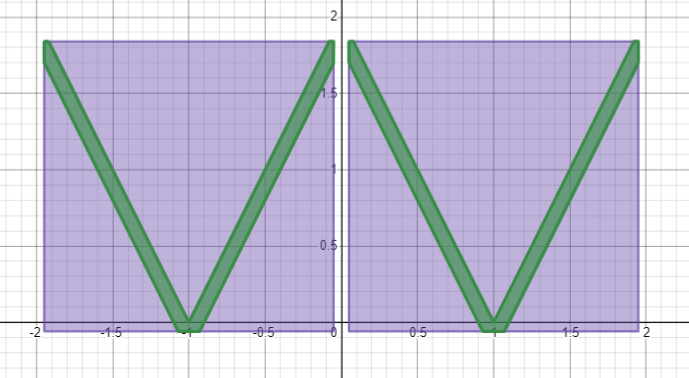
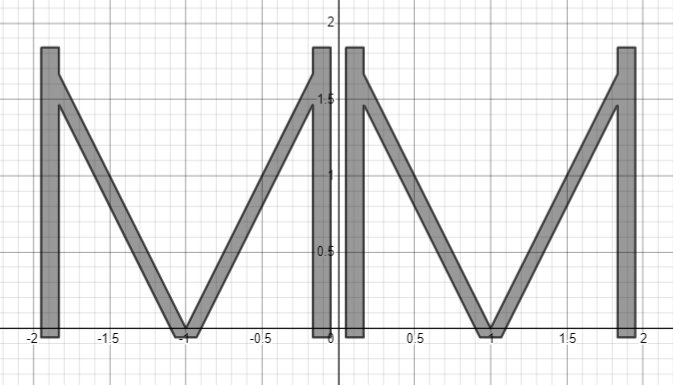
""
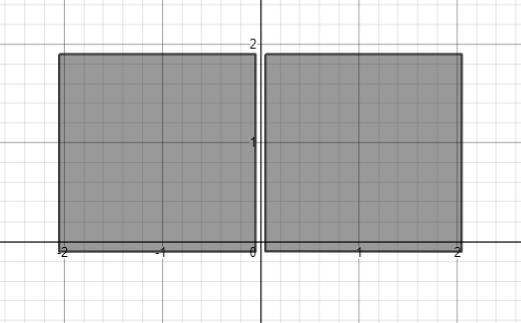

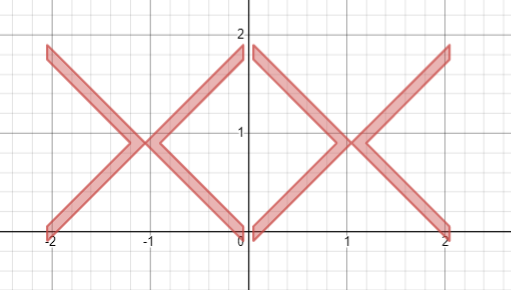
4.1 ,
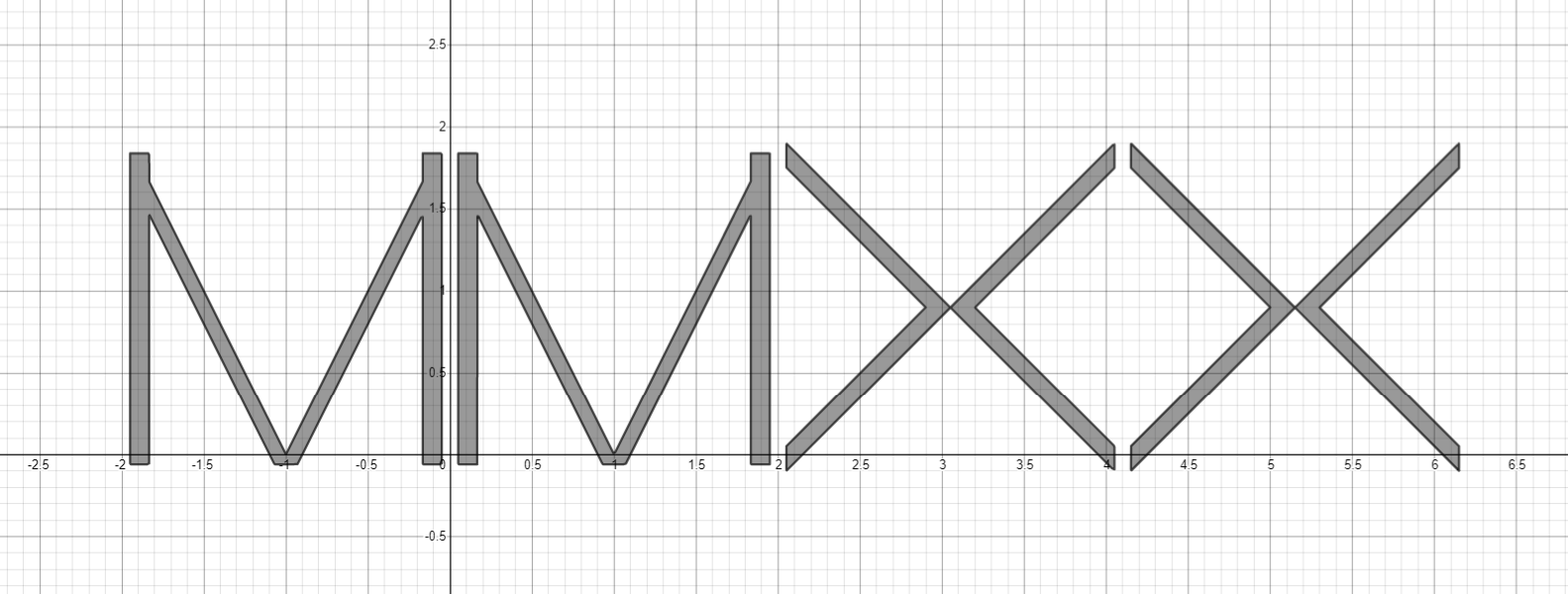
"I"
, "I"
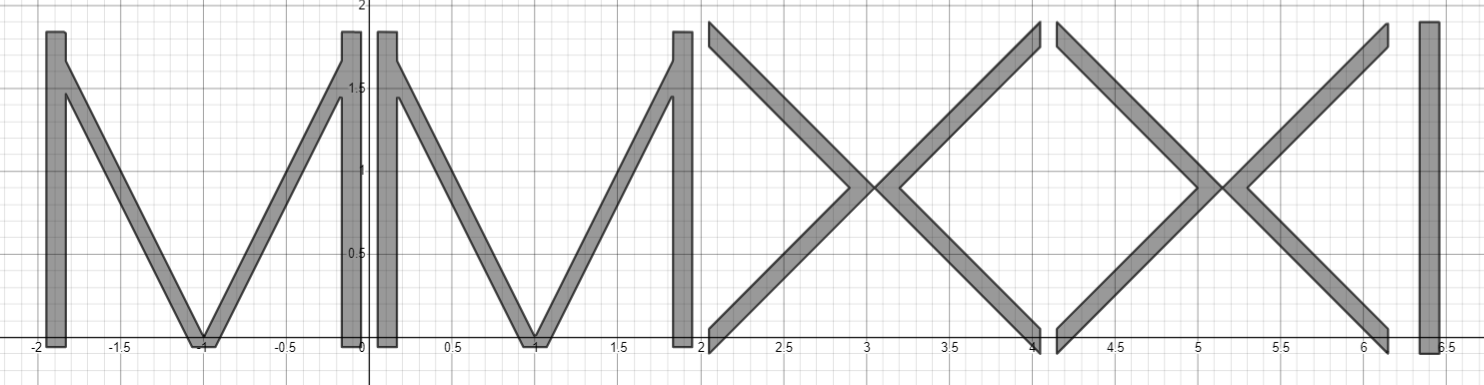
t_{2}=\max\left(\left|\left|x_{1}\right|-1\right|,\left|y_{1}-0.89\right|\right)-0.95
\max\left(\min\left(-t_{2},\max\left(\left|1.2\left|x_{1}\right|-1.2\right|,\left|y_{1}-0.9\right|\right)-1\right),\min\left(\left|2\left|x_{1}\right|-2\right|-y_{1},-\left|2\left|x_{1}\right|-2\right|+y_{1}+0.2,-t_{2}\right)\right)\ge0
\max\left(-\min\left(\left|\left|x_{1}-4.1\right|-1.05\right|-\left|y_{1}-0.9\right|,\ -\left|\left|x_{1}-4.1\right|-1.05\right|+\left|y_{1}-0.9\right|+0.15\right),\max\left(\left|\left|x_{1}-4.1\right|-1.05\right|,\left|y_{1}-0.9\right|\right)-1\right)\le0

, - , , , sin(x), x∈(-5, 5). .
:
Therefore, using the min and max functions in figure formulas is legal in this task.