💆🏿 👩🏼‍🎓 🎖️ How to make a Christmas tree if you are a mathematician 🕡 🤞🏾 👌🏽

Happy New Year 2021 to Habr and Habrazhateli and present to all of us such an unpretentious and pleasant Functional Christmas tree (fYolka). In this article I will tell you how to make a Christmas tree on the monitor in 10 minutes. I will devote my second article to how to "mold" a snowman, put gifts under the tree and sprinkle it all with snow on top.

Basic idea

The whole figure is a set of mathematical functions from two arguments, x and y. All of them are based on SDF in one way or another . Desmos.com was used to draw the graphs .

Basic functions

Zero limit

$x + \ left | x \ right |$

Ellipse

$\ frac {\ left (x-2 \ right) ^ {2}} {3} + \ frac {\ left (y-3 \ right) ^ {2}} {1} = 1$

Christmas tree

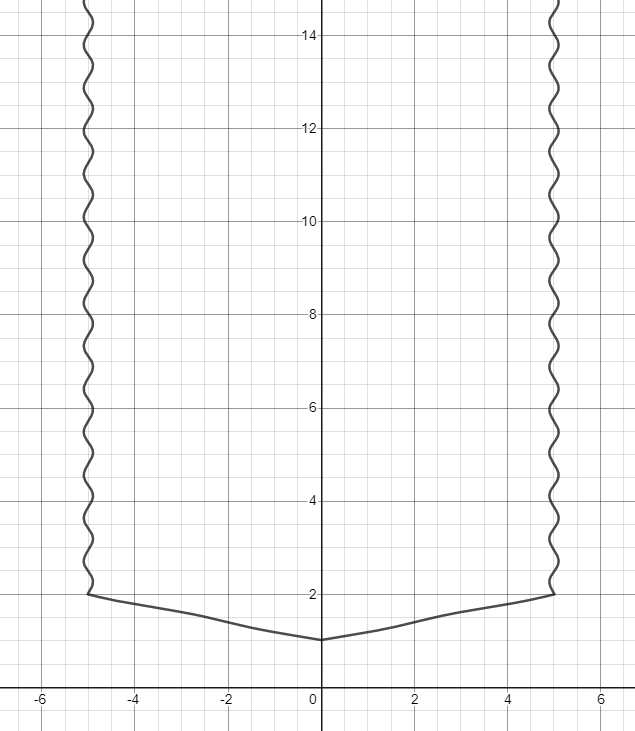
Let's describe the basis of the tree

$- \ left (y-13 \ right) -2 \ left | x \ right | = 0$

Add branches

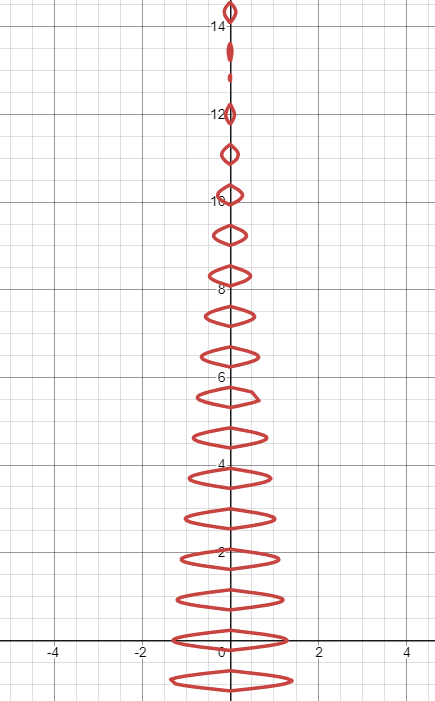
$-0.2 \ cos \ left (6.8y \ right) \ left (y-13 \ right) -2 \ left | x \ right | = 0$

Bring the tips of the branches to the ground

$-0.2 \ cos \ left (6.8y + 0.7 \ left | x \ right | \ right) \ left (y-13 \ right) -2 \ left | x \ right | = 0$

Limit the spruce from above

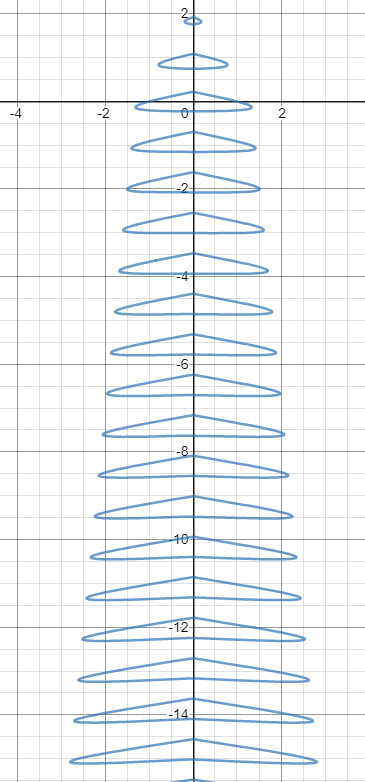
Spruce moved down, this will be corrected later

Parallel stroke: limit from below

Limiter

$2x = 5 \ left (y- \ left | y-2 \ right | \ right)$

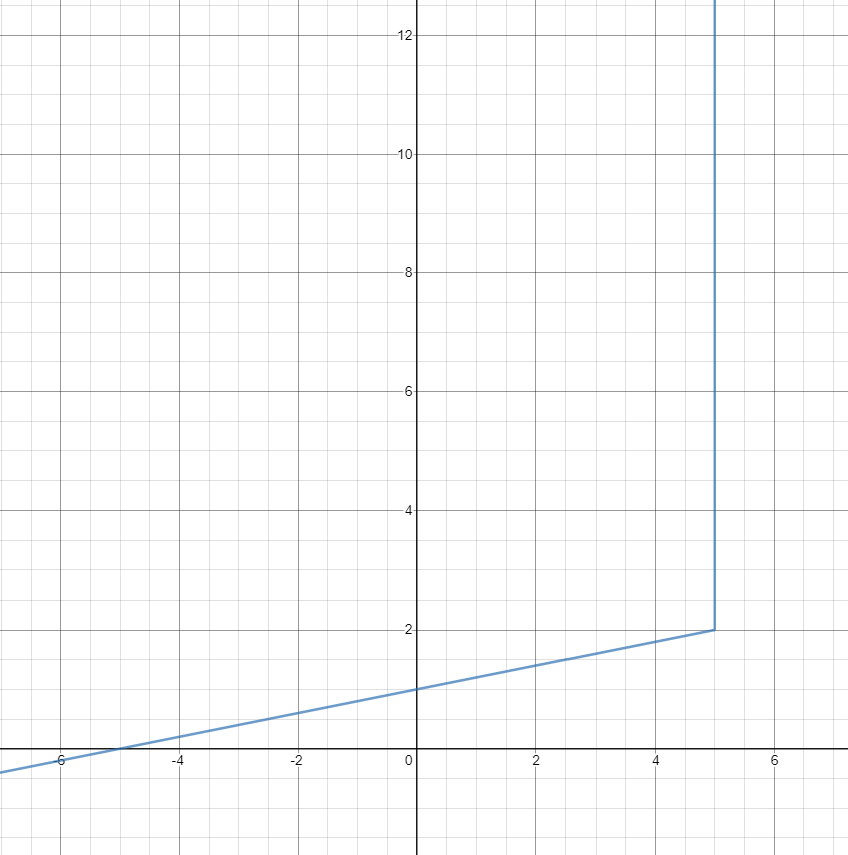
The result of this stage

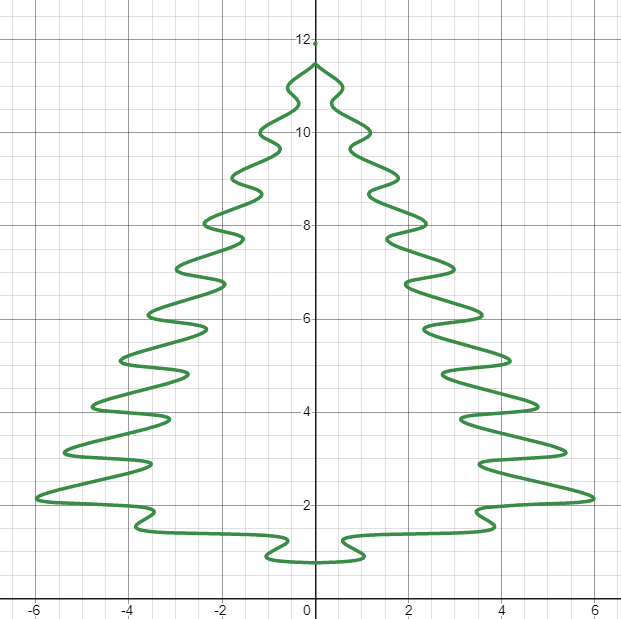
We combine

The final touch

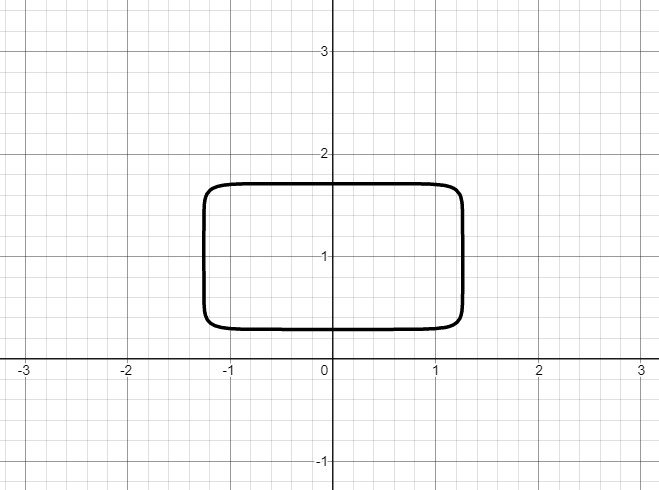
Let's deal with the trunk

Ellipse with sharper corners

$\ 0.1x ^ {10} +30 \ left (y-1 \ right) ^ {10} -1 = 0$

Combining objects

Union, intersection and cut are based on the simplest min (a, b) operation. Depending on the signs in front of a and b, different Boolean operations are obtained.

Foliage - a (xy), trunk - b (xy)

$-a \ le0, b \ le0$

The final

$\ min \ left (-a, b \ right) \ le0$

All formulas to embed in desmos.com

b \ = \ 0.1x ^ {10} +30 \ left (y-1 \ right) ^ {10} -1

\ min \ left (-a, \ b \ right) \ le0

To be continued...

How to make a Christmas tree if you are a mathematician