Splay tree. Search

Hello, Habr! We invite future students of the course "Algorithms and Data Structures" to an open webinar on the topic "Reserves of Binary Search Trees."



And now we are sharing with you the traditional translation of useful material.

---

, , , (Binary Search Tree) O(n). , . O(log n) - -.

, , - -?

- -, Splay- ( ) . splay- , , , , , O(1) . , ( 80% 20% ). , , , .

splay- O(log n), n - . (n).

 

splay- , ( — splay). , . , NULL.

:

1. . , , , , .

2. Zig: ( ). ( ), ( ).

T1, T2 T3 — y () x ()

3. , . :

) Zig-Zig Zag-Zag. , ( ) , ( ).

) Zig-Zag Zag-Zig. , ( ) , ( ).

:

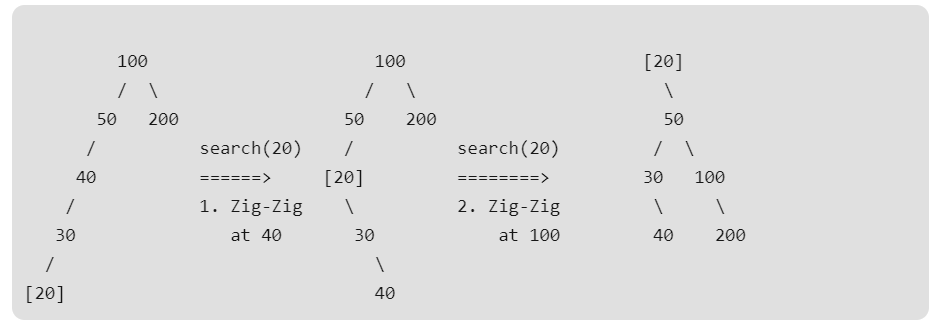
, (splay) , . , 1.

:

C++

#include <bits/stdc++.h> 
using namespace std; 

// An AVL tree node 
class node 
{ 
	public: 
	int key; 
	node *left, *right; 
}; 

/* Helper function that allocates 
a new node with the given key and 
	NULL left and right pointers. */
node* newNode(int key) 
{ 
	node* Node = new node(); 
	Node->key = key; 
	Node->left = Node->right = NULL; 
	return (Node); 
} 

// A utility function to right 
// rotate subtree rooted with y 
// See the diagram given above. 
node *rightRotate(node *x) 
{ 
	node *y = x->left; 
	x->left = y->right; 
	y->right = x; 
	return y; 
} 

// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
node *leftRotate(node *x) 
{ 
	node *y = x->right; 
	x->right = y->left; 
	y->left = x; 
	return y; 
} 

// This function brings the key at 
// root if key is present in tree. 
// If key is not present, then it 
// brings the last accessed item at 
// root. This function modifies the 
// tree and returns the new root 
node *splay(node *root, int key) 
{ 
	// Base cases: root is NULL or 
	// key is present at root 
	if (root == NULL || root->key == key) 
		return root; 

	// Key lies in left subtree 
	if (root->key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root->left == NULL) return root; 

		// Zig-Zig (Left Left) 
		if (root->left->key > key) 
		{ 
			// First recursively bring the 
			// key as root of left-left 
			root->left->left = splay(root->left->left, key); 

			// Do first rotation for root, 
			// second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root->left->key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring 
			// the key as root of left-right 
			root->left->right = splay(root->left->right, key); 

			// Do first rotation for root->left 
			if (root->left->right != NULL) 
				root->left = leftRotate(root->left); 
		} 

		// Do second rotation for root 
		return (root->left == NULL)? root: rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root->right == NULL) return root; 

		// Zag-Zig (Right Left) 
		if (root->right->key > key) 
		{ 
			// Bring the key as root of right-left 
			root->right->left = splay(root->right->left, key); 

			// Do first rotation for root->right 
			if (root->right->left != NULL) 
				root->right = rightRotate(root->right); 
		} 
		else if (root->right->key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of 
			// right-right and do first rotation 
			root->right->right = splay(root->right->right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root->right == NULL)? root: leftRotate(root); 
	} 
} 

// The search function for Splay tree. 
// Note that this function returns the 
// new root of Splay Tree. If key is 
// present in tree then, it is moved to root. 
node *search(node *root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print 
// preorder traversal of the tree. 
// The function also prints height of every node 
void preOrder(node *root) 
{ 
	if (root != NULL) 
	{ 
		cout<<root->key<<" "; 
		preOrder(root->left); 
		preOrder(root->right); 
	} 
} 

/* Driver code*/
int main() 
{ 
	node *root = newNode(100); 
	root->left = newNode(50); 
	root->right = newNode(200); 
	root->left->left = newNode(40); 
	root->left->left->left = newNode(30); 
	root->left->left->left->left = newNode(20); 

	root = search(root, 20); 
	cout << "Preorder traversal of the modified Splay tree is \n"; 
	preOrder(root); 
	return 0; 
} 

// This code is contributed by rathbhupendra 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

C

// The code is adopted from http://goo.gl/SDH9hH 
#include<stdio.h> 
#include<stdlib.h> 

// An AVL tree node 
struct node 
{ 
	int key; 
	struct node *left, *right; 
}; 

/* Helper function that allocates a new node with the given key and 
	NULL left and right pointers. */
struct node* newNode(int key) 
{ 
	struct node* node = (struct node*)malloc(sizeof(struct node)); 
	node->key = key; 
	node->left = node->right = NULL; 
	return (node); 
} 

// A utility function to right rotate subtree rooted with y 
// See the diagram given above. 
struct node *rightRotate(struct node *x) 
{ 
	struct node *y = x->left; 
	x->left = y->right; 
	y->right = x; 
	return y; 
} 

// A utility function to left rotate subtree rooted with x 
// See the diagram given above. 
struct node *leftRotate(struct node *x) 
{ 
	struct node *y = x->right; 
	x->right = y->left; 
	y->left = x; 
	return y; 
} 

// This function brings the key at root if key is present in tree. 
// If key is not present, then it brings the last accessed item at 
// root. This function modifies the tree and returns the new root 
struct node *splay(struct node *root, int key) 
{ 
	// Base cases: root is NULL or key is present at root 
	if (root == NULL || root->key == key) 
		return root; 

	// Key lies in left subtree 
	if (root->key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root->left == NULL) return root; 

		// Zig-Zig (Left Left) 
		if (root->left->key > key) 
		{ 
			// First recursively bring the key as root of left-left 
			root->left->left = splay(root->left->left, key); 

			// Do first rotation for root, second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root->left->key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring the key as root of left-right 
			root->left->right = splay(root->left->right, key); 

			// Do first rotation for root->left 
			if (root->left->right != NULL) 
				root->left = leftRotate(root->left); 
		} 

		// Do second rotation for root 
		return (root->left == NULL)? root: rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root->right == NULL) return root; 

		// Zag-Zig (Right Left) 
		if (root->right->key > key) 
		{ 
			// Bring the key as root of right-left 
			root->right->left = splay(root->right->left, key); 

			// Do first rotation for root->right 
			if (root->right->left != NULL) 
				root->right = rightRotate(root->right); 
		} 
		else if (root->right->key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of right-right and do first rotation 
			root->right->right = splay(root->right->right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root->right == NULL)? root: leftRotate(root); 
	} 
} 

// The search function for Splay tree. Note that this function 
// returns the new root of Splay Tree. If key is present in tree 
// then, it is moved to root. 
struct node *search(struct node *root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print preorder traversal of the tree. 
// The function also prints height of every node 
void preOrder(struct node *root) 
{ 
	if (root != NULL) 
	{ 
		printf("%d ", root->key); 
		preOrder(root->left); 
		preOrder(root->right); 
	} 
} 

/* Driver program to test above function*/
int main() 
{ 
	struct node *root = newNode(100); 
	root->left = newNode(50); 
	root->right = newNode(200); 
	root->left->left = newNode(40); 
	root->left->left->left = newNode(30); 
	root->left->left->left->left = newNode(20); 

	root = search(root, 20); 
	printf("Preorder traversal of the modified Splay tree is \n"); 
	preOrder(root); 
	return 0; 
} 

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

Java

// Java implementation for above approach 
class GFG 
{ 

// An AVL tree node 
static class node 
{ 

	int key; 
	node left, right; 
}; 

/* Helper function that allocates 
a new node with the given key and 
	null left and right pointers. */
static node newNode(int key) 
{ 
	node Node = new node(); 
	Node.key = key; 
	Node.left = Node.right = null; 
	return (Node); 
} 

// A utility function to right 
// rotate subtree rooted with y 
// See the diagram given above. 
static node rightRotate(node x) 
{ 
	node y = x.left; 
	x.left = y.right; 
	y.right = x; 
	return y; 
} 

// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
static node leftRotate(node x) 
{ 
	node y = x.right; 
	x.right = y.left; 
	y.left = x; 
	return y; 
} 

// This function brings the key at 
// root if key is present in tree. 
// If key is not present, then it 
// brings the last accessed item at 
// root. This function modifies the 
// tree and returns the new root 
static node splay(node root, int key) 
{ 
	// Base cases: root is null or 
	// key is present at root 
	if (root == null || root.key == key) 
		return root; 

	// Key lies in left subtree 
	if (root.key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root.left == null) return root; 

		// Zig-Zig (Left Left) 
		if (root.left.key > key) 
		{ 
			// First recursively bring the 
			// key as root of left-left 
			root.left.left = splay(root.left.left, key); 

			// Do first rotation for root, 
			// second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root.left.key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring 
			// the key as root of left-right 
			root.left.right = splay(root.left.right, key); 

			// Do first rotation for root.left 
			if (root.left.right != null) 
				root.left = leftRotate(root.left); 
		} 

		// Do second rotation for root 
		return (root.left == null) ? 
							root : rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root.right == null) return root; 

		// Zag-Zig (Right Left) 
		if (root.right.key > key) 
		{ 
			// Bring the key as root of right-left 
			root.right.left = splay(root.right.left, key); 

			// Do first rotation for root.right 
			if (root.right.left != null) 
				root.right = rightRotate(root.right); 
		} 
		else if (root.right.key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of 
			// right-right and do first rotation 
			root.right.right = splay(root.right.right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root.right == null) ? 
							root : leftRotate(root); 
	} 
} 

// The search function for Splay tree. 
// Note that this function returns the 
// new root of Splay Tree. If key is 
// present in tree then, it is moved to root. 
static node search(node root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print 
// preorder traversal of the tree. 
// The function also prints height of every node 
static void preOrder(node root) 
{ 
	if (root != null) 
	{ 
		System.out.print(root.key + " "); 
		preOrder(root.left); 
		preOrder(root.right); 
	} 
} 

// Driver code 
public static void main(String[] args) 
{ 
	node root = newNode(100); 
	root.left = newNode(50); 
	root.right = newNode(200); 
	root.left.left = newNode(40); 
	root.left.left.left = newNode(30); 
	root.left.left.left.left = newNode(20); 

	root = search(root, 20); 
	System.out.print("Preorder traversal of the" + 
					" modified Splay tree is \n"); 
	preOrder(root); 
} 
} 

// This code is contributed by 29AjayKumar 

      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

C#

// C# implementation for above approach 
using System; 

class GFG 
{ 

// An AVL tree node 
public class node 
{ 

	public int key; 
	public node left, right; 
}; 

/* Helper function that allocates 
a new node with the given key and 
null left and right pointers. */
static node newNode(int key) 
{ 
	node Node = new node(); 
	Node.key = key; 
	Node.left = Node.right = null; 
	return (Node); 
} 

// A utility function to right 
// rotate subtree rooted with y 
// See the diagram given above. 
static node rightRotate(node x) 
{ 
	node y = x.left; 
	x.left = y.right; 
	y.right = x; 
	return y; 
} 

// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
static node leftRotate(node x) 
{ 
	node y = x.right; 
	x.right = y.left; 
	y.left = x; 
	return y; 
} 

// This function brings the key at 
// root if key is present in tree. 
// If key is not present, then it 
// brings the last accessed item at 
// root. This function modifies the 
// tree and returns the new root 
static node splay(node root, int key) 
{ 
	// Base cases: root is null or 
	// key is present at root 
	if (root == null || root.key == key) 
		return root; 

	// Key lies in left subtree 
	if (root.key > key) 
	{ 
		// Key is not in tree, we are done 
		if (root.left == null) return root; 

		// Zig-Zig (Left Left) 
		if (root.left.key > key) 
		{ 
			// First recursively bring the 
			// key as root of left-left 
			root.left.left = splay(root.left.left, key); 

			// Do first rotation for root, 
			// second rotation is done after else 
			root = rightRotate(root); 
		} 
		else if (root.left.key < key) // Zig-Zag (Left Right) 
		{ 
			// First recursively bring 
			// the key as root of left-right 
			root.left.right = splay(root.left.right, key); 

			// Do first rotation for root.left 
			if (root.left.right != null) 
				root.left = leftRotate(root.left); 
		} 

		// Do second rotation for root 
		return (root.left == null) ? 
							root : rightRotate(root); 
	} 
	else // Key lies in right subtree 
	{ 
		// Key is not in tree, we are done 
		if (root.right == null) return root; 

		// Zag-Zig (Right Left) 
		if (root.right.key > key) 
		{ 
			// Bring the key as root of right-left 
			root.right.left = splay(root.right.left, key); 

			// Do first rotation for root.right 
			if (root.right.left != null) 
				root.right = rightRotate(root.right); 
		} 
		else if (root.right.key < key)// Zag-Zag (Right Right) 
		{ 
			// Bring the key as root of 
			// right-right and do first rotation 
			root.right.right = splay(root.right.right, key); 
			root = leftRotate(root); 
		} 

		// Do second rotation for root 
		return (root.right == null) ? 
							root : leftRotate(root); 
	} 
} 

// The search function for Splay tree. 
// Note that this function returns the 
// new root of Splay Tree. If key is 
// present in tree then, it is moved to root. 
static node search(node root, int key) 
{ 
	return splay(root, key); 
} 

// A utility function to print 
// preorder traversal of the tree. 
// The function also prints height of every node 
static void preOrder(node root) 
{ 
	if (root != null) 
	{ 
		Console.Write(root.key + " "); 
		preOrder(root.left); 
		preOrder(root.right); 
	} 
} 

// Driver code 
public static void Main(String[] args) 
{ 
	node root = newNode(100); 
	root.left = newNode(50); 
	root.right = newNode(200); 
	root.left.left = newNode(40); 
	root.left.left.left = newNode(30); 
	root.left.left.left.left = newNode(20); 

	root = search(root, 20); 
	Console.Write("Preorder traversal of the" + 
				" modified Splay tree is \n"); 
	preOrder(root); 
} 
} 

// This code is contributed by 29AjayKumar 
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

:

Preorder traversal of the modified Splay tree is 20 50 30 40 100 200

1) Splay- . . .

2) splay- O(log n). , Splay- O(log n) ( , )

3) Splay- - -, splay- .

4) -, splay- , .

Splay-

Splay- , 30 , .

Splay- Windows NT ( , ), gcc GNU C++, sed, Fore Systems, Unix malloc, Linux (: http://www.cs.berkeley.edu/~jrs/61b/lec/36)

Splay Tree | Set 2 (Insert).

:

http://www.cs.berkeley.edu/~jrs/61b/lec/36

http://www.cs.cornell.edu/courses/cs3110/2009fa/recitations/rec-splay.html

http://courses.cs.washington.edu/courses/cse326/01au/lectures/SplayTrees.ppt

---

" ".



" ."

OTUS . .   OTUS.

, " " -   .