While studying the Algorithms on Strings course, I faced the problem of building a suffix tree . Following the link for additional materials, I came across a recommendation to "view this great comment on Stack Overflow ". Having studied and implemented according to the given free description , Ukkonen's algorithm decided to share the translation.
Below is an attempt to describe Ukkonen's algorithm; first showing how it works on a simple string (i.e. the string contains no duplicate characters), gradually expanding to the complete algorithm.
A few preliminary statements:
What we are building is basically a prefix tree . This is the root vertex, whose edges go out of it to new vertices, and subsequent edges go out of them, and so on.
But , unlike a prefix tree, edge labels are not single characters, for each edge the label is a pair of numbers [from, to] - pointers to positions in the text. In this case, each edge contains a string of arbitrary length, but only takes O (1) memory (two pointers)
Basic principle
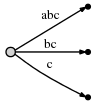
First, the author wants to demonstrate how to create a suffix tree of an extremely simple string, strings without duplicate characters:
abc
The algorithm works in steps, from left to right . One step per line character . Each step may involve more than one individual operation, but we will see (see final observations at the end) that the total number of operations is O (n).
a
, [0, #]
- 0 . #
, , 1 ( a
).
, :
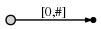
:

2 ( b
). : . :
a
-ab
b
:
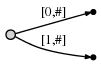
:
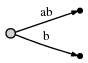
:
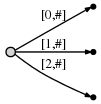
ab
, :[0, #]
. ,#
1 2.
O(1) , , , .
c
c
.
:
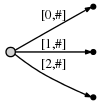
:
:
,
O(n),
#
, O(1). n, O(n)
:
, , . :
abcabxabcd
abc
, , ab
x
, abc
d
.
1 3: 3 :
4: #
4. :

a
.
, ( #
), , , , :
(_, _, _)
,
, :
abc
(, '\0x', 0)
, .._
,_
'0\x',_
. , , , .
1 . , , , 1 ( )
. a
, a
, : abca
. :
[3, #]
. ,a
. , - . , .
(, 'a', 1)
. , -a
, , 1 . ,a
. , ( , , ).
, 2
Spoiler
[4, #]
, , a
3
: , , , (
). , ( a
). , ( , O(1)), .
5: #
5. :
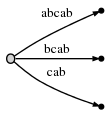
,
2, : ab
b
. - , :
a
. , ,
ab
.
b
.
, ( a
, abcab
), b
. : , b
.
, . :
(, 'a', 2)
( , ,b
)
3, , .
: ab
b
, ab
, b
. ? , ab
, ( b
) . , , , - , .
6, #
. :
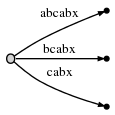
3, abx
, bx
x
. , ab
, x
. , x
, abcabx
:

- , O(1).
, abx
2. bx
. , . , , 1, , _
( 3 ).
1, :
-
_
-
_
, , ..b
-
_
1
C, (, 'b', 1)
, bcabx
, 1 , b
. O(1) , x
. , . x
, , :
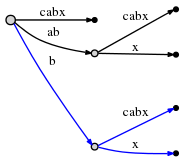
O(1),
1, (, 'x', 0)
, 1.
-. 2:
, , , , .
Spoiler
1 2
, , , , .
, . ( ):

, x
. _
0, . x
, :
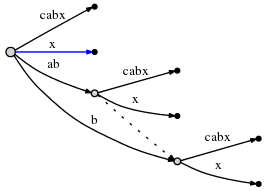
Spoiler
, .
7, #
= 7, , , a
. () , . , , (, 'a', 1)
.
Spoiler
#
, , #
8, #
= 8, b
, , , , (, 'a', 2)
, , b
. ( O(1)), . (1, '\0x', 0)
. 1
, ab
.
, #
= 9 'c', :
:
, #
c
, , , 'c'. , 'c' , (1, 'c', 1)
,
.
#
= 10
4, abcd
( 3 ), d
.
d
O(1):

_
, , .
3
_
, , , ,_
, . ,_
._
_
.
(2, 'c', 1)
, 2 :
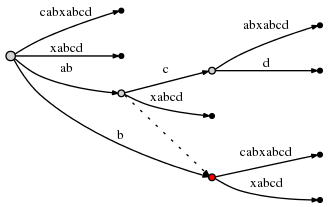
abcd
,
3 : bcd
. 3 , bcd
, d
.
, - 2 :
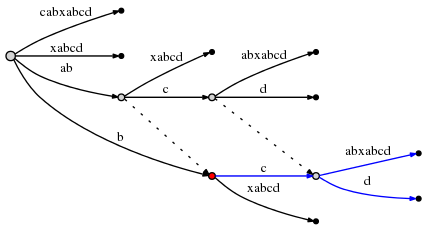
: , O(1). , , ab
b
( ), abc
bc
.
.
2, 3, . _
( ) , . (, 'c', 1)
.
, , c
: cabxabcd
, , c
. :
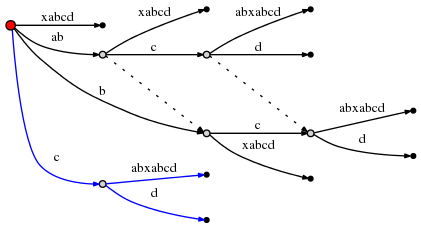
, 2 :
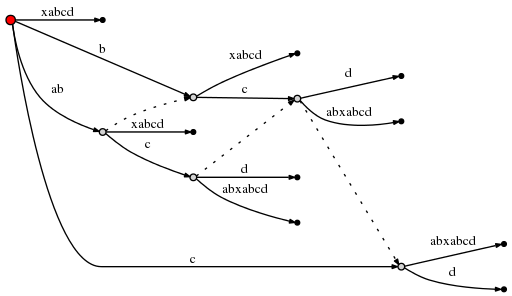
( Graphviz Dot . , , , , - )
1, _
, 1 (root, 'd', 0)
. , d
:
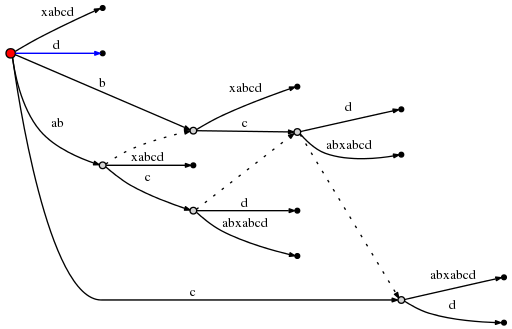
Spoiler
, . :
#
1 . O(1).
:
,
.
, . , #
. . : O(1), , , . ? ( , ).
, , , , ,
> 0. , , . , . ,
> 0, , .
Spoiler
,
> 0? , - , - . , . $
. ? → , , . , , .
- , , , . , , , .
? n , , n ( n + 1, ). ( ),
, O(1) .
, , , , , -, n ( n + 1). , O(n).
, : , , , , _
_
. , :
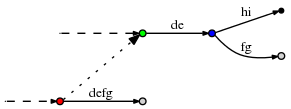
( . )
, (, 'd', 3)
, f
defg
. , , 3. (, 'd', 3)
. d
-, - de
, 2 . , , , (, 'f', 1)
.
_
,
, n. , , , , , n . , O(n2),
O(n), - _
O(n)?
. , (, , ), , , _
. , , , _
, , , , _
. _
,
,
O(n) , , -
O(n), O(n).
Translator notes
In general, the algorithm is described in an easy and understandable language. Following the description, it is possible to implement it, and natural optimizations will happen on the fly. I highlighted the places that caused difficulties for me with spoilers.
In my implementation , the ACGT alphabet is used, since it pursued the goal of passing tests for a problem within a course.