Mathematical Olympiad. William Lowell Putnam Mathematical Competition is a mathematical competition for undergraduate students studying at universities (colleges) in the United States and Canada. The inspiration for the Olympics was William Lowell Putnam, an American lawyer and banker. Held by the Mathematical Association of America annually since 1938. Cash prizes are awarded to the top five varsity teams ($ 25,000 first place prize) and the twenty-five top students in the individual competition ($ 1,000 first place prize).
- Wikipedia
The Olympiad lasts two times for 3 hours, 12 problems in total, 10 points for each. The average mark that students gain is 1 or 2. Let's consider one of the most difficult problems from this Olympiad.
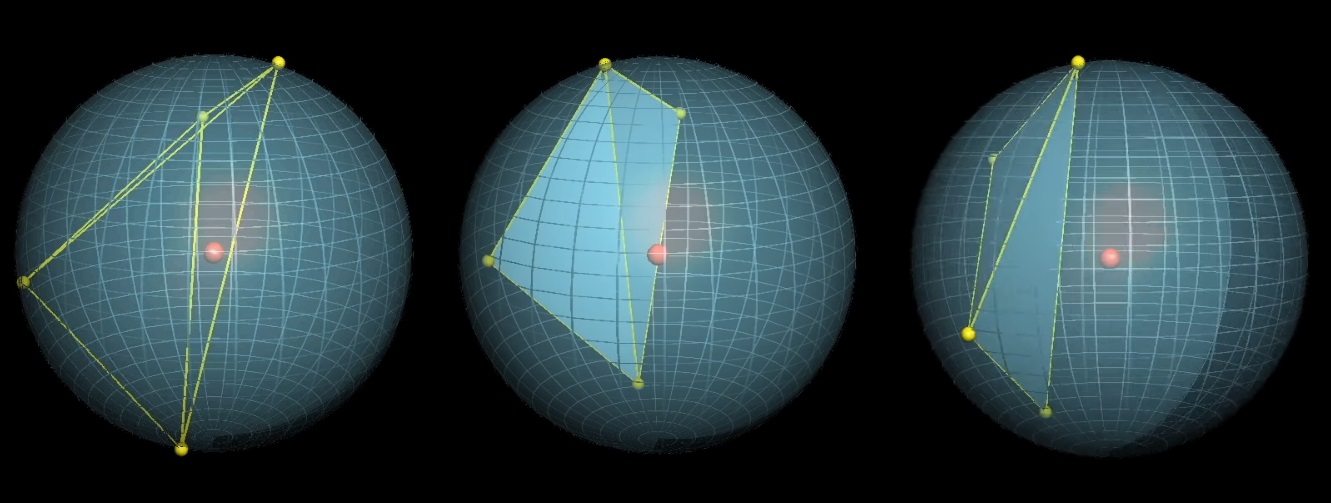
Choose 4 random points on the sphere. What is the probability that the center of the sphere will be inside the tetrahedron formed by these points?
Let's consider a two-dimensional version of this problem.
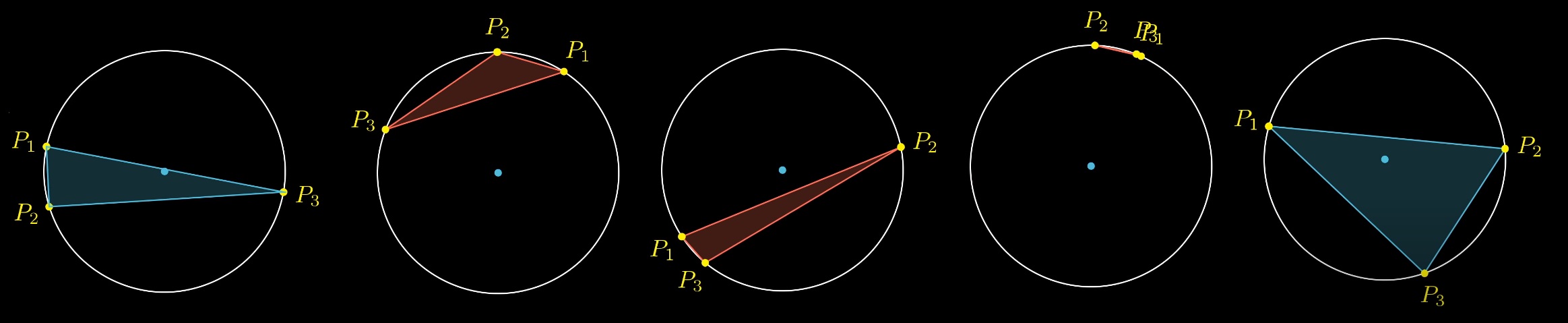
Consider 3 random points on a circle. What is the probability that the center of the circle will be inside the triangle?

You can fix two points and play with the third. It is easy to see that there is a certain zone, the projection of the anchored points relative to the center, inside which the third point must fall in order for the condition to be met. The circle is thus divided into 4 parts. The probability of hitting the third point in the arc is equal to the ratio of the arc length to the circumference. How long is the arc?
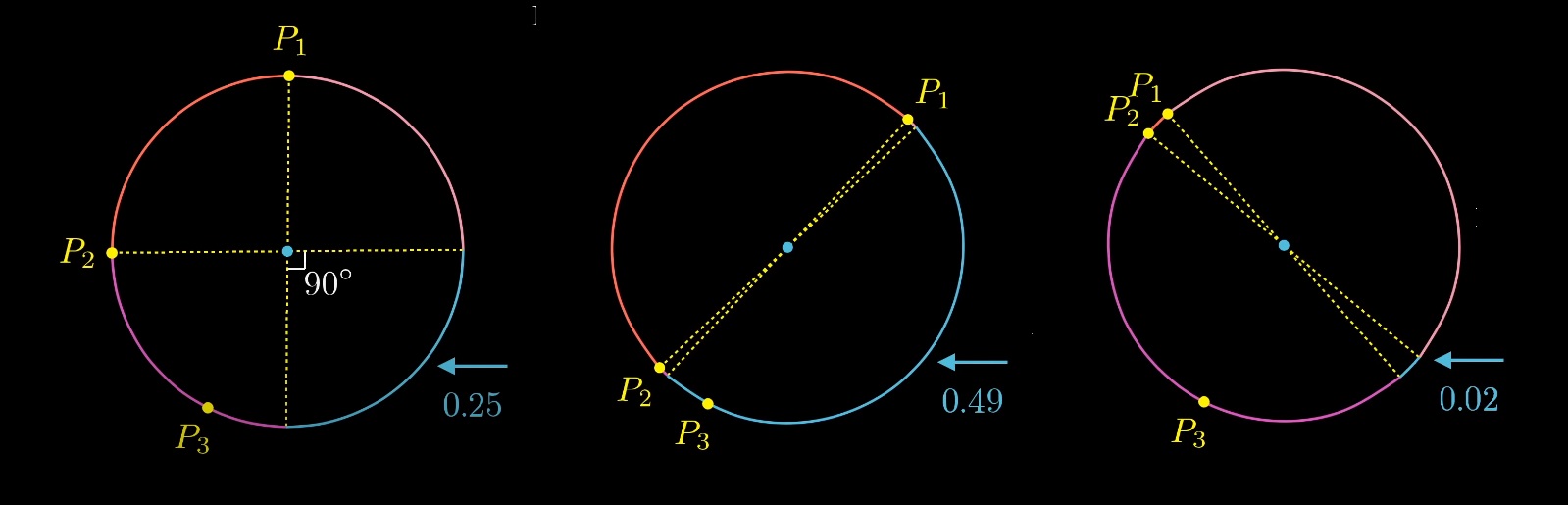
The probability ranges from 0 to 0.5 depending on the location of the first two points.
What is the average probability?

Let's fix the first point and play with the second. The probability will vary from 0 to 0.5, that is, the average probability will be 0.25.
Solving the problem for a circle and three points - 25%.
Is it possible to transfer this approach to a sphere and 4 points?
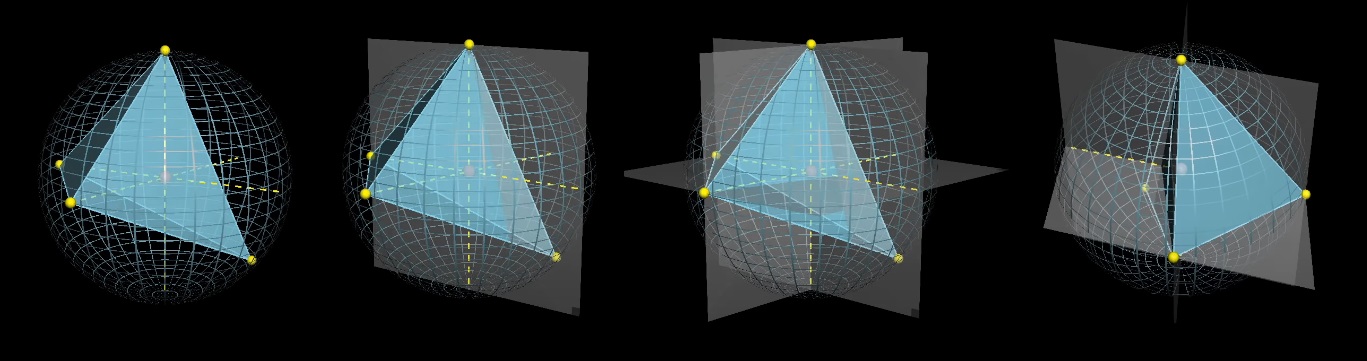
We fix three points and play with the fourth. Let's draw projections of fixed points relative to the center and divide the sphere into 8 parts with planes.
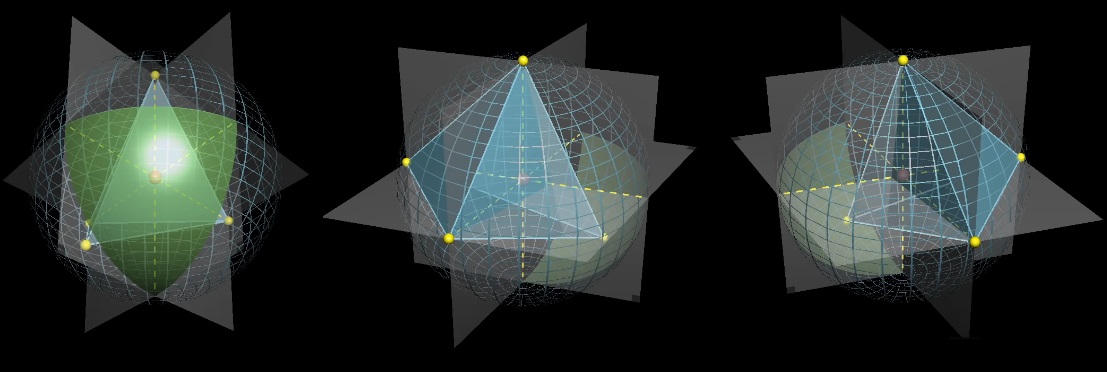
The center of the sphere will be inside the tetrahedron if the fourth point falls on the green spherical triangle, which is "opposite" the fixed points relative to the center. What is the average green section size?
// Don't think of anything further, improvise.
You can go back to the two-dimensional case and think about where 1/4 came from. Where does 4 come from?
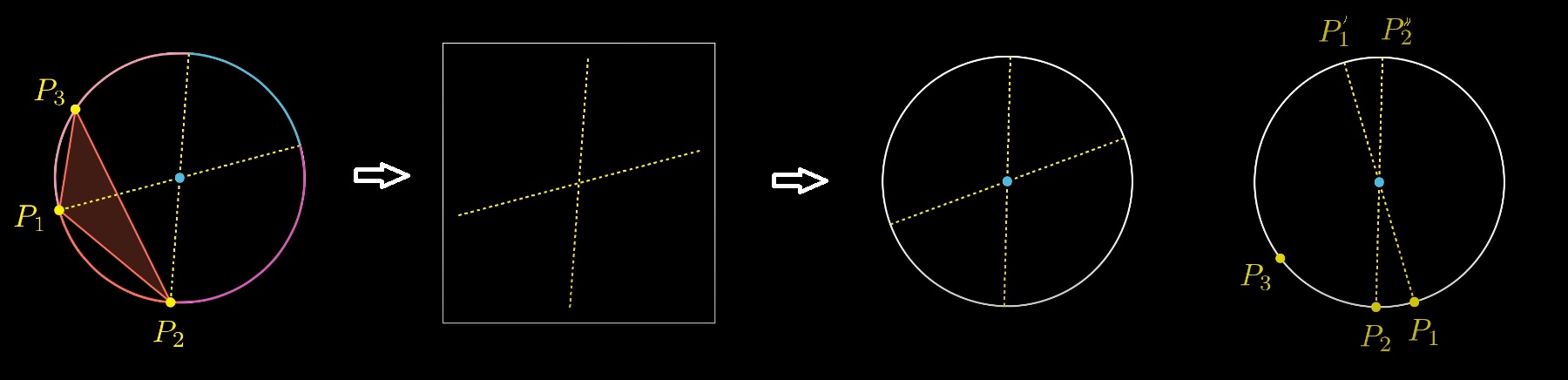
You can go from 3 random points on a circle to another problem. Let's choose two random diameters. Then, for each diameter, we throw a coin, thereby choosing where the point Pi will be, from which end of the diameter. Then we randomly choose the third point on the circle.
And then another cunning move.
Let's first select the third point at random and then randomly select two diameters. We will have 4 options for placing points P2 P1:
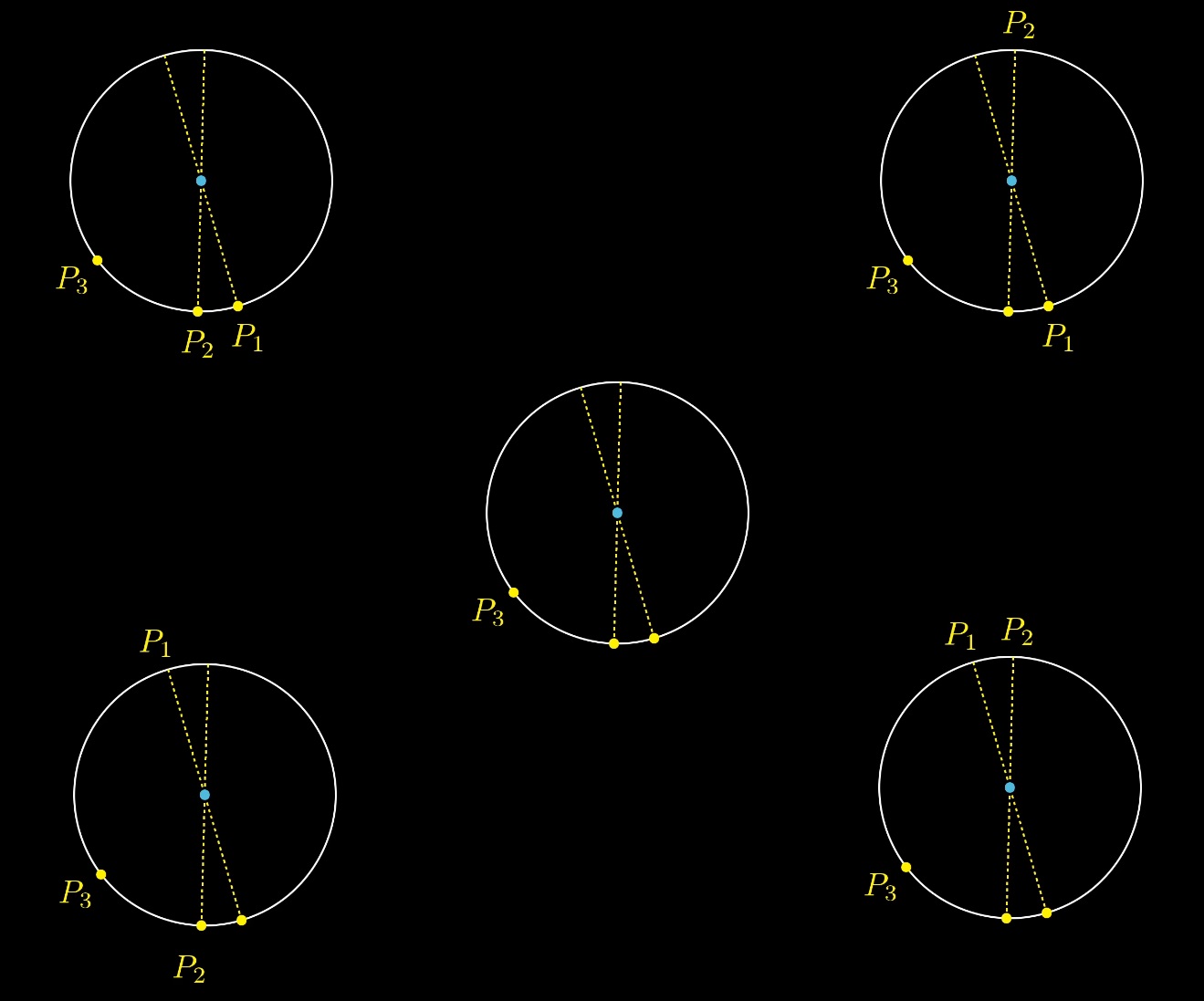
But only one of these 4 options contains a solution when the center of the circle is inside the triangle:
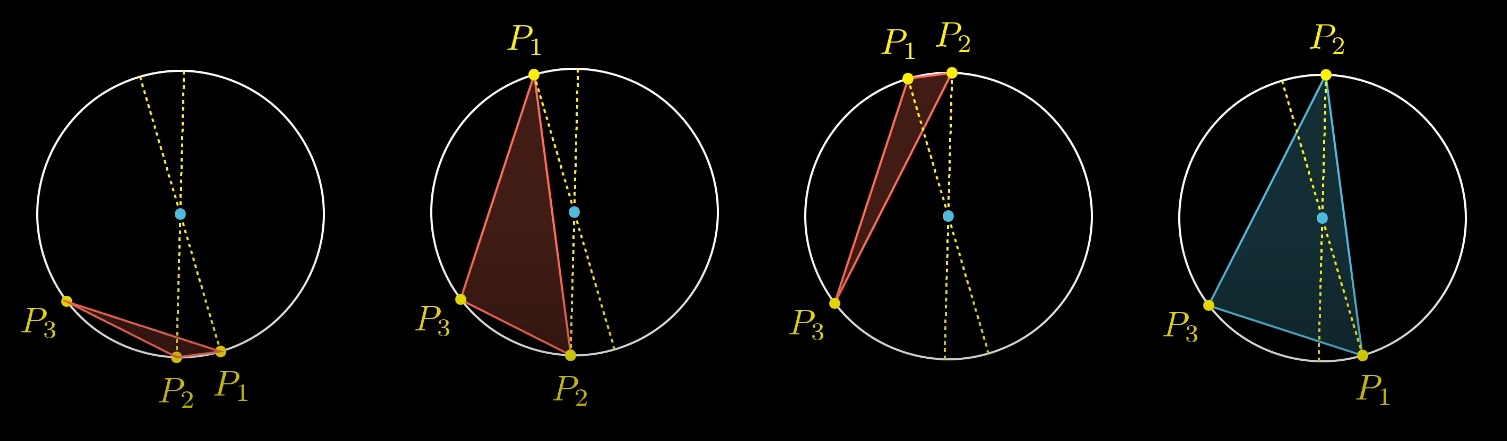
Whichever we choose the random starting position of the third point and two diameters, only one of the options contains the center of the circle inside the triangle:

That's how we reformulated the problem:

With a sphere, we get 8 options for choosing points, after fixing the first point and choosing three diameters:
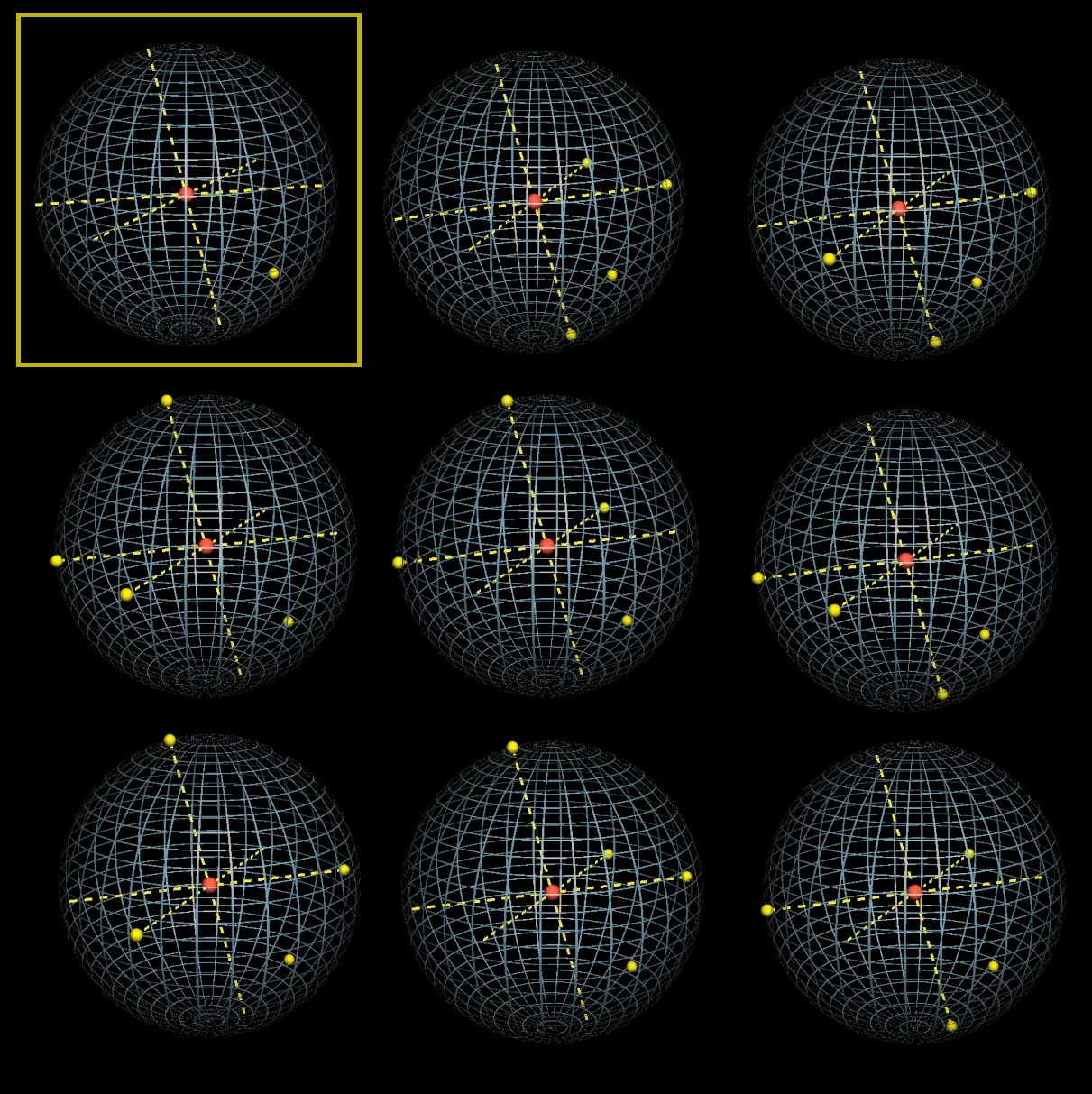
Only 1 of 8 satisfies the condition that the center of the sphere is inside the tetrahedron:
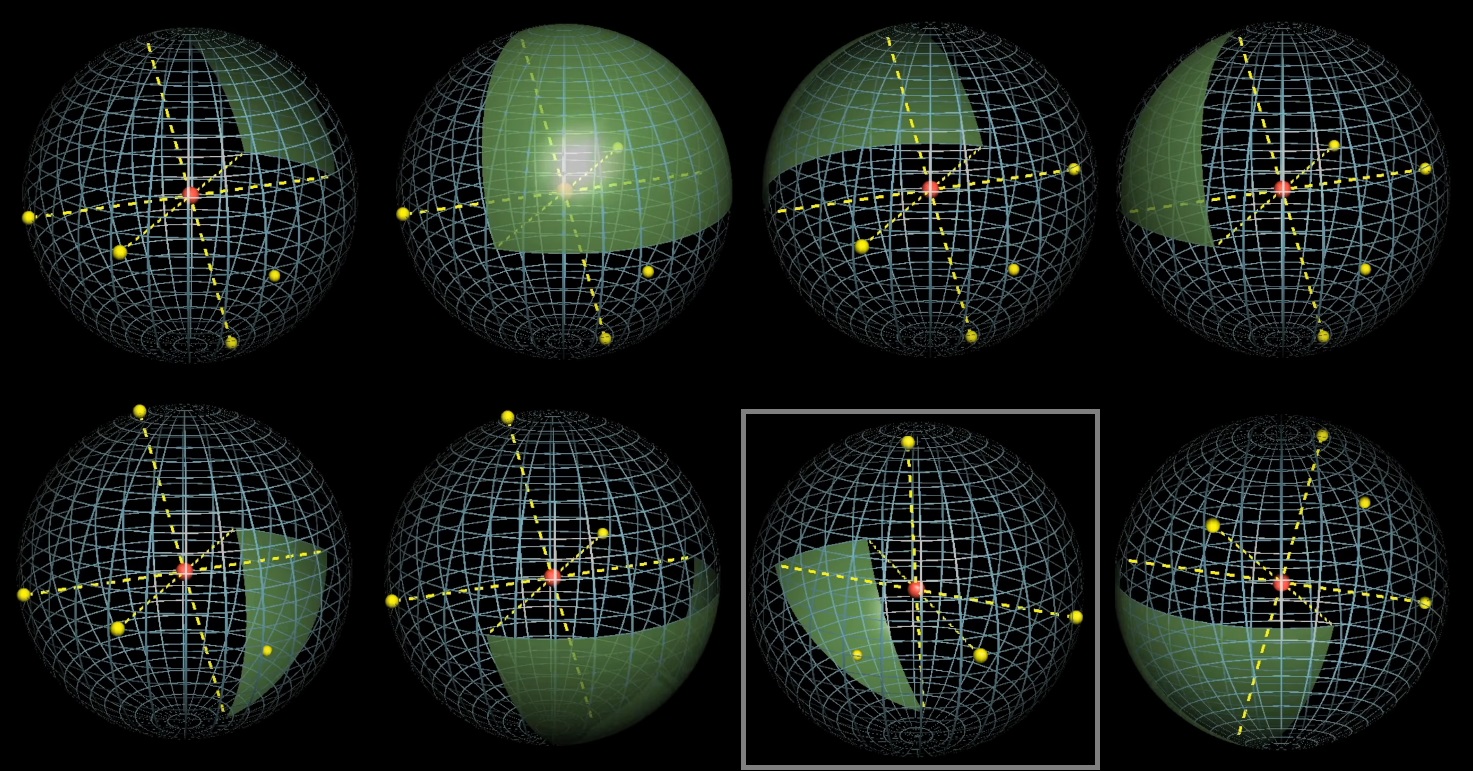
Answer: 1/8
- Hardcore linear algebra is here: Capturing the Origin with Random Points: Generalizations of a Putnam Problem
- All the problems of the 1992 Olympiad: The 53rd William Lowell Putnam Mathematical Competition
Saturday, December 5, 1992