
So, consider a directed weighted graph. Let the graph have n vertices. Each pair of vertices corresponds to some weight (transition probability).

It should be noted that typical web graphs are a homogeneous discrete Markov chain for which the indecomposability condition and the aperiodicity condition are satisfied.
Let us write the Kolmogorov-Chapman equation:
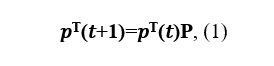
where P is the transition matrix.
Suppose there is a limit. The
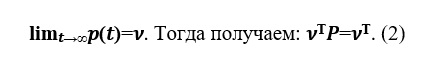
vector v is called a stationary probability distribution.
It was from relation (2) that it was proposed to search for the ranking vector of web pages in the Brin-Page model.
Since v is the limit,

the stationary distribution can be calculated by the method of simple iterations (MPI).
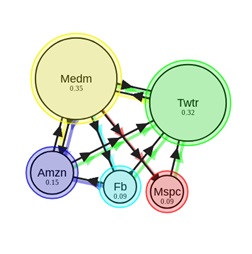
In order to go from one web page to another, the user must, with a certain probability, choose which link to go to. If the document has several outgoing links, then we will assume that the user clicks on each of them with the same probability. And finally, there is also the teleportation coefficient, which shows us that with some probability the user can move from the current document to another page, not necessarily directly related to the page in which we are at the moment. Let the user teleport with probability δ, then equation (1) will take the form

For 0 <δ <1, the equation is guaranteed to have a unique solution. In practice, an equation with δ = 0.15 is usually used to calculate PageRank.
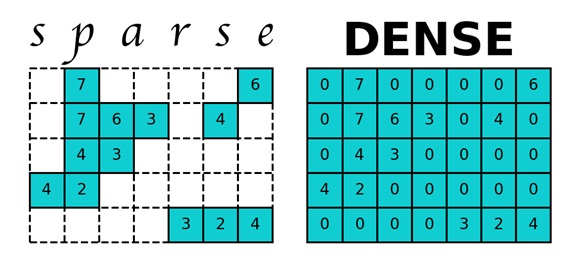
Consider a Google web graph from a site - link. This web graph contains 875713 vertices, which means that for a two-dimensional matrix P, you need to allocate 714 Gb of memory. The RAM of modern computers is an order of magnitude less, so the computer begins to use hard disk memory, access to which greatly slows down the work of the PageRank calculation program. But the matrix P is a sparse matrix - a matrix with predominantly zero elements. To work with sparse matrices in Python, the sparse module from the scipy library is used, which helps the matrix P to take up much less memory.
Let's apply this algorithm to this data. Nodes are web pages, and directed edges are hyperlinks between them.
First, let's import the libraries we need:
import cvxpy as cp
import numpy as np
import pandas as pd
import time
import numpy.linalg as ln
from scipy.sparse import csr_matrix
Now let's move on to the implementation itself:
#
data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="\t", header=None)
NODES = 916428
EDGES = 5105039
#
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
b = NEW.sum(axis=1)
NEW = NEW.transpose()
#
p0 = np.ones((NODES,1))/NODES
eps = 10**-5
delta = 0.15
ERROR = True
k = 0
#
while (ERROR == True):
with np.errstate(divide='ignore'):
z = p0 / b
p1 = (1-delta) * NEW.dot(csr_matrix(z)) + delta * np.ones((NODES,1))/NODES
if (ln.norm(p1-p0) < eps):
ERROR = False
k = k + 1
# PageRank
p0 = p1
On the graphs we can see how the vector p comes to a stationary state v :

Using the PageRank vector, you can also determine the winner in the elections. A small subset of Wikipedia contributors are administrators, who are users with access to additional technical features to aid in maintenance. In order for a user to become an administrator, an administrator request is issued, and the Wikipedia community, through public comment or voting, decides who to promote to the administrator position.
The PageRank problem can also be reduced to a minimization problem and solved using the Frank – Wolfe conditional gradient method, which is as follows: select one of the vertices of the simplex and make a starting point at this vertex. Implementation of this method on data - the link is presented below:
#
data = pd.read_csv("grad.txt", names = ['i','j'], sep="\t", header=None)
NODES = 6301
EDGES = 20777
#
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
b = NEW.sum(axis=1)
NEW = NEW.transpose()
e = np.ones(NODES)
with np.errstate(divide='ignore'):
z = e / b
NEW = NEW.dot(csr_matrix(z))
#
eps = 0.05
k=0
a_0 = 1
y = np.zeros((NODES,1))
p0 = np.ones((NODES,1))/NODES
#
p0[0] = 0.1
y[np.argmin(df(p0))] = 1
p1 = (1-2/(1+k))*p0 + 2/(1+k)*y
#
while ((ln.norm(p1-p0) > eps)):
y = np.zeros((NODES,1))
k = k + 1
p0 = p1
y[np.argmin(df(p0))] = 1
p1 = (1-2/(1+k))*p0 + 2/(1+k)*y

For the effective operation of a real search engine, the speed of calculating the PageRank vector is more important than the accuracy of its calculation. MPI does not allow you to sacrifice accuracy for the sake of computation speed. The Monte Carlo algorithm helps to some extent cope with this problem. We launch a virtual user who wanders through the pages of the sites. By collecting statistics of their visits to the pages of the site, after a fairly long period of time we get for each page how many times the user has visited it. By normalizing this vector, we get the desired PageRank vector. Let us demonstrate how this algorithm works on data already in use .
#
def get_edges(m, i):
if (i == NODES):
return random.randint(0, NODES)
else:
if (len(m.indices[m.indptr[i] : m.indptr[i+1]]) != 0):
return np.random.choice(m.indices[m.indptr[i] : m.indptr[i+1]])
else:
return NODES
#
data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="\t", header=None)
NODES = 916428
EDGES = 5105039
NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES))
#c , total –
for total in range(1000000,2000000,100000):
#
k = random.randint(0, NODES)
# PageRank
ans = np.zeros(NODES+1)
margin2 = np.zeros(NODES)
ans_prev = np.zeros(NODES)
for t in range(total):
j = get_edges(NEW, k)
ans[j] = ans[j]+1
k = j
#
ans = np.delete(ans, len(ans)-1)
ans = ans/sum(ans)
for number in range(len(ans)):
margin2[number] = ans[number] - ans_prev[number]
ans_prev = ans
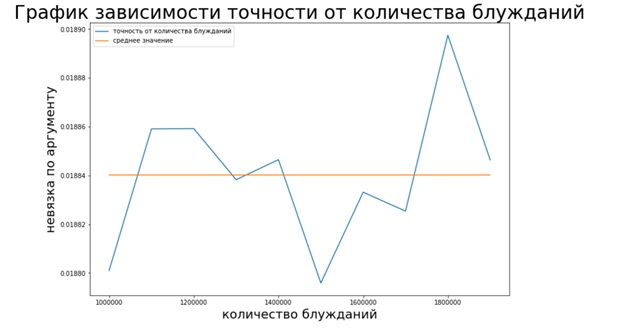
As can be seen from the graph, the Monte Carlo method, unlike the two previous methods, is not stable (there is no convergence), however, it helps to estimate the Page Rank vector without requiring much time.
Conclusion: Thus, we have considered the main algorithms for determining the PageRank of web graphs. Before you start designing a website, you should make sure that PageRank is not wasted by paying attention to the following things:
- Internal links show how “link power” is accumulating on your site, so focus on the important information on the home page of the site, as the “home” page of the site has the strongest PageRank.
- Orphan pages that are not linked from other pages on your site. Try to avoid such pages.
- It is worth mentioning external links if they are of benefit to your site visitor.
- Broken inbound links dilute the overall weight of the page, so you need to periodically monitor them and “fix” them if necessary.
However, this does not mean that you should be obsessed with PageRank. But it is worth remembering that by paying attention to the structure of the site when building it, the features of internal and external links, you are optimizing the site for PageRank.