
Good day!
In the modern world, there are more and more statements about the potential threat from quantum computers in relation to the cryptography protocols used. The quantum computer is already capable of solving the problems of discrete logarithm and factorization of a number, which threatens all protocols based on them.
Today we will consider the NewHope protocol, which is based on another difficult task - the problem of learning with errors in a ring (Ring-LWE).
NewHope – , , . , SIS, LWE Ring-LWE:
1. SIS
SIS (Short integer solution problem) – .
, n q ( ):
A:

( ) , .
, ,
. , , .
, z,
. z ( q). , , . , .
? , ( ).
- . z.
, z A .
, , n - .
2. LWE ( Learning with errors)
:
:
n – ;
q – , . n, ;
, );
;
k, .
, , s
. ( q):
.
, (LWE on lattices).
:

– .
, q. .
, , :
:
.
3.
LWE, - SIS:
Public key encryption (LWE):
, . – .

,
0, 0, 1.
?
.
, , 4 , .
One-way function (SIS):
- -:

, . . (IV).
, ,
.
- (One-way function):
, :
.
-
:
SIS.
? , SIS .
4.
:
.
15 :

2) / , .
?
5. Ring-LWE
.
? , LWE . , n ?
?
– ,
, n – .
c q.
? . , , : . .
/? , 2 ,
LWE , , .
6. NewHope
, NewHope , Bos, Castello, Naehrig Stebila. TLS Ring-LWE.
, NewHope.
, .

:
, .
n = 1024, q = 12289 ( ,
). NTT ( ), n – , q – , .
a. : seed – 256 , SHAKE-128 ( SHA3). , 1024 a. : , TLS ( 2 ), NewHope , a. , backdoor , “” .
– , . - , ( ). seed /dev/urandom 16- . s e.
( b, seed).
a, s’, e’, e”, u.
v, , . .
,
, , . , – , 0
. , .
. : . q ,
.
( ).
. .
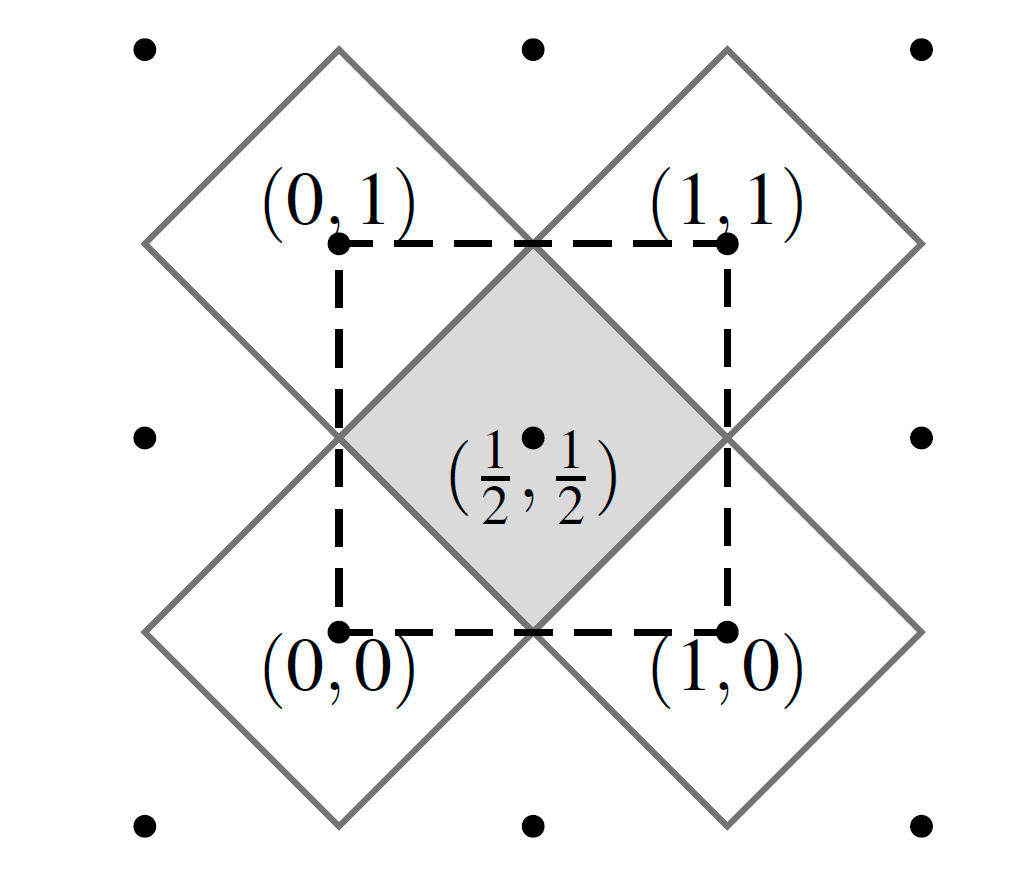
. , , : , 1, , 0. , , . HelpRec, . . , , .
8. Rec 1 4 ( ).
9. 256 , , .
7.
2019 NIST post-quantum crypto project, , . NIST , , KYBER ( Module-LWE) , . 3 KYBER.
, Google Canary CECPQ1 CECPQ2.
:
Haskell
FPGA
:
https://newhopecrypto.org/
https://eprint.iacr.org/2015/1092.pdf
https://eprint.iacr.org/2014/599.pdf
https://www.di.ens.fr/chloe.hebant/presentation/SISproblem.pdf
http://www.ee.cityu.edu.hk/~twhk05/achieve/Wai%20Ho%20Mow.pdf
https://simons.berkeley.edu/talks/lwe-worst-case-average-case-reductions-and-cryptomania
https://simons.berkeley.edu/talks/algebraic-lattices-and-ring-lwe
https://www.ei.ruhr-uni-bochum.de/media/sh/veroeffentlichungen/2013/08/14/lwe_encrypt.pdf
https://summerschool-croatia.cs.ru.nl/2018/slides/Introduction%20to%20post-quantum%20cryptography%20and%20learning%20with%20errors.pdf
https://people.csail.mit.edu/vinodv/6876-Fall2015/L12.pdf
https://security.googleblog.com/2016/07/experimenting-with-post-quantum.html