
We used to rely on modern encryption algorithms. However, are they really that securely protecting our data? Let's take a look at the concept of a mathematical backdoor, what it is and how it works.
Introduction
Over the past decades, the world community has confidently moved towards the development of civil liberties. The right to confidential privacy, privacy of correspondence - these phrases have been on our ears for a long time.
, , , , , .
, . , , .
Inspiration
?
, . , . , , , . , , . .
.
, :
. : ( ) . .
, , , , , () . SSH. « », . «», « » .
.

, :
, , , . , , .
, . , AES, . - , Backdoored Encryption Algorithm 1, BEA-1 . , .
, . , «implementation backdoors», . , , , «» .
Recent years have shown that more than ever governments and intelligence agencies try to control and bypass the cryptographic means used for the protection of data. Backdooring encryption algorithms is considered as the best way to enforce cryptographic control. Until now, only implementation backdoors (at the protocol, implementation or management level) are generally considered.
, . , .
In this paper we propose to address the most critical issue of backdoors: mathematical backdoors or by-design backdoors, which are put directly at the mathematical design of the encryption algorithm. While the algorithm may be totally public, proving that there is a backdoor, identifying it and exploiting it, may be an intractable problem.
, :
— , , , ,
— , , ,
— , , ,
— - , .
. BEA-1, , , .
Considering a particular family (among all the possible ones), we present BEA-1, a block cipher algorithm which is similar to the AES and which contains a mathematical backdoor enabling an operational and effective cryptanalysis. The BEA-1 algorithm (80-bit block size, 120-bit key, 11 rounds) is designed to resist to linear and differential cryptanalyses.
, — , , .
, , . .
. , DUAL_EC_DRBG - , TLS - («implementation backdoos»).
DUAL_EC_DRBG
DUAL_EC_DRBG - NIST 2006 . 2007 , . .
A concrete example is the pseudorandom number generator Dual_EC_DBRG designed by NSA, whose backdoor was revealed by Edward Snowden in 2013 and also in some research works.
TLS Apple
TLS Apple. , , - .
static DSStatus SSLVerifySignedServerKeyExchnge(....)
{
DSStatus err;
....
if ((err = SSLHashSHA1.update(&hashCtx, &signedParams)) != 0)
goto fail;
goto fail;
if ((SSHashSHA1.final(&hashCtx, &hashOut)) != 0)
goto fail;
....
fail:
....
return err;
}
, if goto fail, , if. . , , . "Man-in-the-middle", . , , , . , , - .
, , .
BEA-1?
, , , . - . . , , Substitution-Permutation Networks, .
SP - , S-, P- XOR . S-, P-. , P- . , , , . , S P .
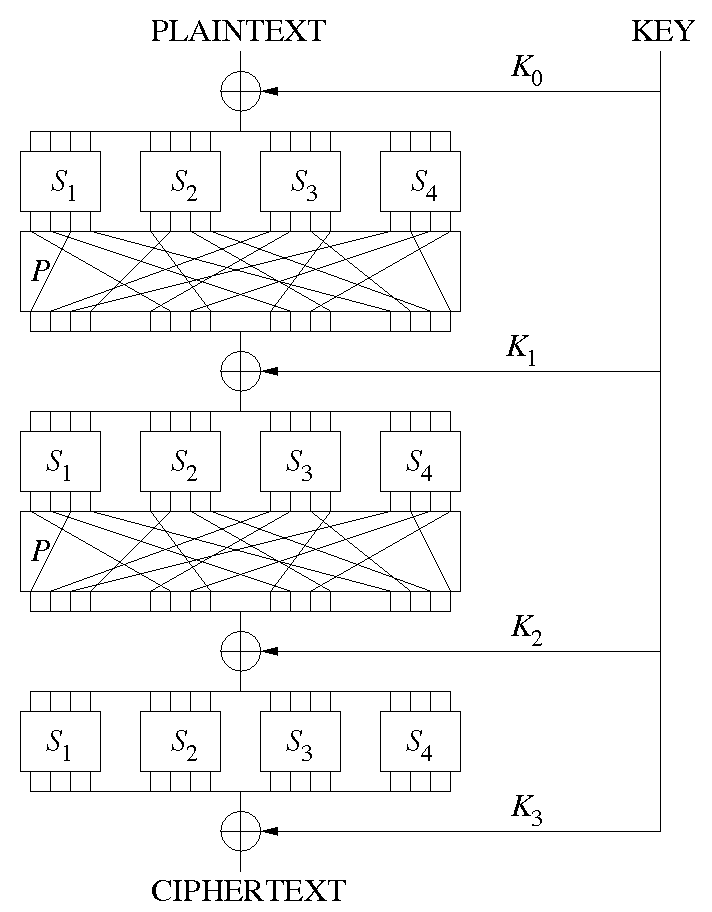
SP- , (. substitution stage) (. permutation stage). , S P . ( ). , P .
S-, . S-, P-. S- . , . S- , . S- , . S- .

P- — : S-, S- . P- S- S- . , P- - , , .
, , . . , - . " ".
, S P ( ) . , . .
, : , :
S-
P-
XOR
P-, .
, . , . , . , S- .
BEA-1
, BEA-1, SP .
:
The encryption consists in applying eleven times a simple keyed operation called /round function/to the data block. A different 80-bit round key is used for each iteration of the round function. Since the last round is slightly different and uses two round keys, the encryption requires twelve 80-bit round keys. These round keys are derived from the 120-bit master key using an algorithm called key schedule
BEA-1, « » . , , 80 , ( ) 2^80.
Consequently, a differential cryptanalysis of the 10-round version of our cipher would require at least 2^117 chosen plaintext/ciphertext pairs and a linear cryptanalysis would require 2^100 known plaintext/ciphertext pairs.
S-
BEA-1 «Secret S-boxes», S-. S- , .
, S- S-, . . , S- , S- . , .
, BEA-1 S0, S1, S2 S- 944 ( 1024, 10 ) S3 925 ( 1024)
, S- S-, .
( , ). BEA-1 30.000 , (2 × 300 Kb) , 10 intel Core i7, 4 cores, 2.50GHz.

, , . S P . . , , . , DES «» IBM.
AES, Apple . . Backdoored Encryption Algorithm 1 Rijndael, AES. , S- AES, Rijandel.
AES DES, . , 1970 S- . .
1990 — . S-. S- DES , . , 1970- . . , 1990 .
The best historic example is that of the differential cryptanalysis. Following Biham and Shamir’s seminal work in 1991, NSA acknowledged that it was aware of that cryptanalysis years ago Most of experts estimate that it was nearly 20 years ahead. However a number of non public, commercial block ciphers in the early 90s might have been be weak with respect to differential cryptanalysis.
. , 34.12-2018. , S- , . S- : , .
. @pelbyl . , " S-", . , , . " S-", , , . , . , - S- AES. , .
iPhone 5C iOS 9, A6. 10 . Secure Enclave. . . — 80 . , .
. iOS 2014 . . , . , , . «, », front door. . . .
2020 Pangu Secure Enclave. Jailbreak-.
, Apple . iPhone 5c c -. , , , .
?

: , , , , . , , , - . , S-.
, « ». , , , . , , .
, - . , , . , , , , .
I cannot leave you alone with the growing paranoia and anxiety, therefore, even assuming the situation that all available encryption algorithms are compromised, the possibility of establishing a secure exchange of information still exists, a whole scientific article is even devoted to this . If you want to feel the atmosphere of searching for vulnerabilities in existing encryption algorithms, then I advise you to read this inspiring article .