This article describes in simple words the cryptoalgorithms that are currently relevant Russian information security standards, and selected links to materials that, if desired, will help to understand them deeper. And also, at the end of the article, works with the results of cryptanalysis of one of the most important elements of these algorithms are given.
From news
. , .

2020 « — , », . , . , 2024 , .
, - eSim.
, .
, .
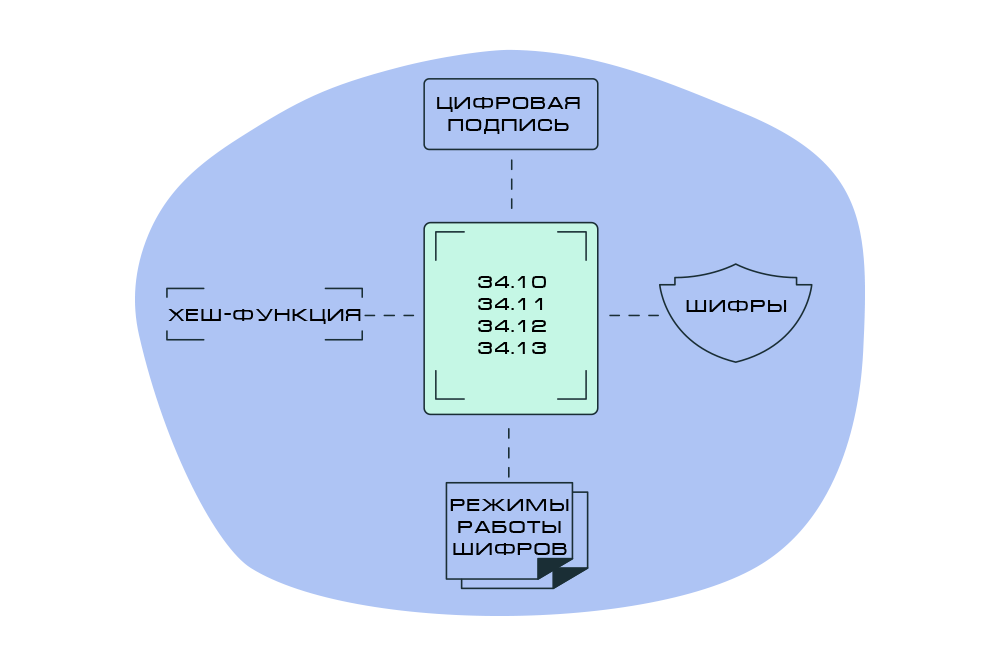
34.10-2018 . 256 512 .
, . , , . , , , .
, , , .
,
,
,
, ( )
,
,
.
, . .
,
, ,
,
,
.
,
.
.
.

:
.
— -() - , , - — .
— ,
— , -
.
,
1.
— , .
— .
— , .
.
.
— ,
.
,
0, .
: .
.
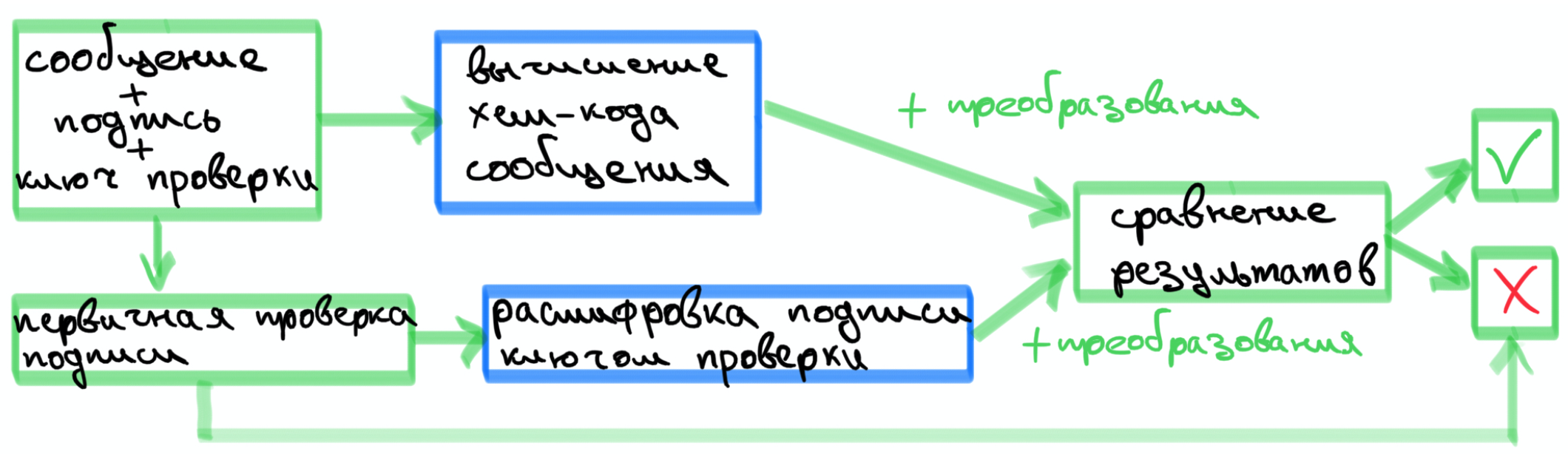
: c
— , , , .
— - , .
— ,
, -
.
,
1.
.
— ,
.
— ,
: /
-
34.11-2018 . -, , .
, 512 ( ). - 256 512 .
34.12-2018 . — 128 64 256 .
10 , , ( ).
.

, , .
32 , , .
, .
34.13-2018 .
. , , . , .

. , .

2, XOR. , , .
, .
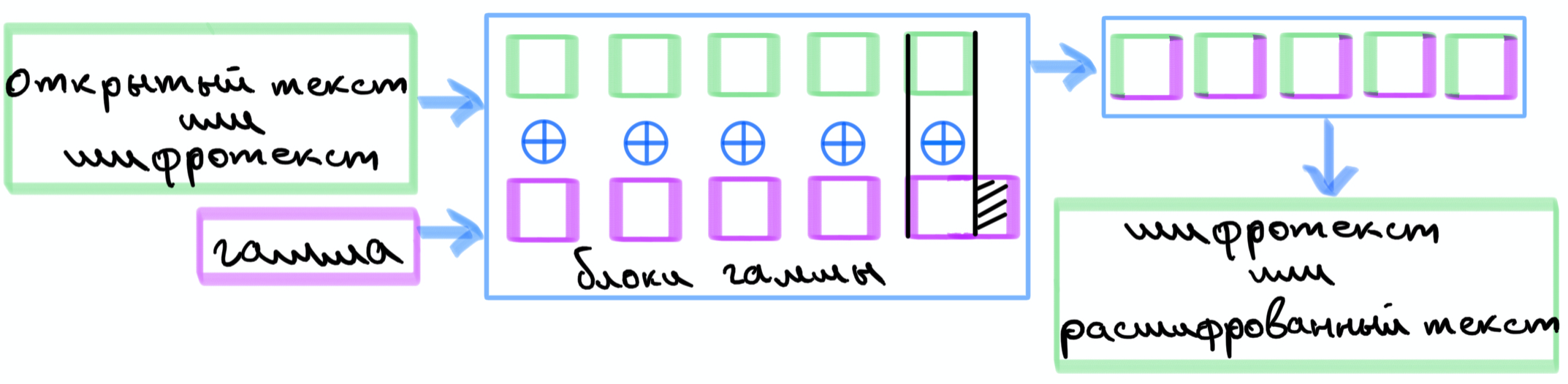
, . .
: ,
, . , , .
.

. , , . .
, , , .
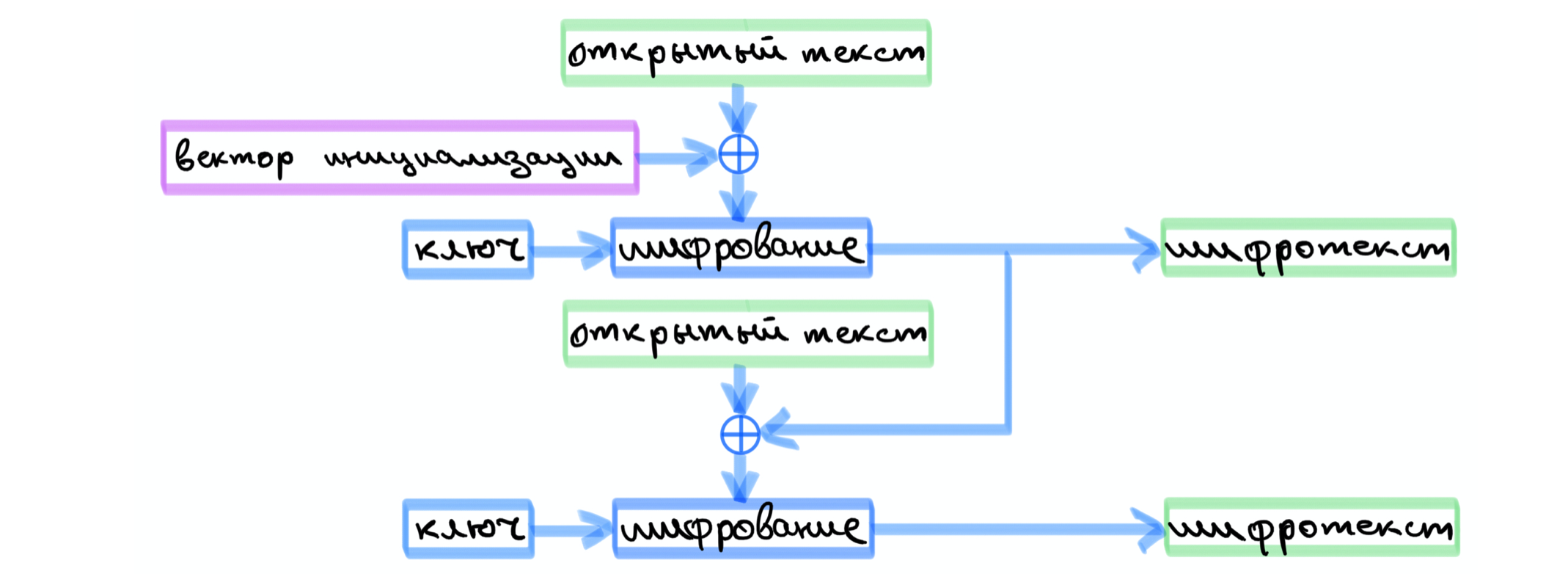
, .
1 2019 . , .
34.10-2018. - , 34.11-2018.
34.12-2018.
. 34.11-2018, .
, . .
, . , .
:
Reverse-Engineering the S-Box of Streebog, Kuznyechik and STRIBOBr1 — Alex Biryukov, L ́eo Perrin, and Aleksei Udovenko
Exponential S-Boxes: a Link Between the S-Boxes of BelT and Kuznyechik/Streebog — Léo Perrin and Aleksei Udovenko
Partitions in the S-Box of Streebog and Kuznyechik — Léo Perrin
, SageMath.
, . , .