Introduction
The most famous cryptographic problem is the transmission of secret messages. For this task, cryptosystems with a private key are most often used: Alice (the sender) encrypts the information using the key, and Bob (the receiver) decrypts the message with it. Unfortunately, private key cryptosystems have serious difficulties in practical implementation. The main question is how to distribute the keys? In many ways, key distribution is just as time-consuming as the basic task of private communication. A malicious third party can eavesdrop on the key and easily read the message.
To avoid this, many ways have been invented, in this article we will consider quantum, in which the secrecy of the key is guaranteed by the laws of quantum mechanics. The first BB84 quantum key distribution (QKD) scheme was developed in 1984 by physicists Charles Bennett and Gilles Brassard. Its main idea is to use the quantum mechanical principle (uncertainty principle), according to which observation as a whole violates the observed system. Thus, the interceptor eavesdropping on Alice and Bob "spoils" the message. Then it can be easily calculated and discarded "bad" bits, and if there are too many of them - start all over again.
The basics of quantum mechanics
We will not go into details, but simply formulate the main statements. Let's start with the uncertainty principle. It says that some physical quantities together are absolutely not exactly measured. Let's cite as an example the momentum and the coordinate of a particle: if you put a particle in a device that accurately measures the coordinate (for example, it showed ), and then in a device that accurately measures the momentum, then the second device will give out a random number (let it be a number
, i.e.
). An important point: before it was a particle with a coordinate
, now it is a particle with momentum
. If you put it back into the device measuring the coordinate, it will give out a random number.
( , , ). , , .
( ), 2 . , , 4 . ,
,
. BB84.
BB84
:
1) ( )
2)
3)
4)
- ; - ; -

1 .
|
|
(0 1). 0 1 | , , . , , , . |
. ( ). , , , . , "" ( ). - - . , . . BB84 11% [10], . .
. : . , , , (, , ). , , "" . : . (, , ). , , . , .
, :
1) , .
2) , .
BB84, , - -. . A B, C. : . A , B , C . , B , , . , A B. . ( ) .
|
|
, , . , . | , . |
, , 0 1.
. BB84 . BB84 , . , .
.
1
1)
2)
3) ,
, , .
1 . , . , , .
2 . . .
3 . - , . , . , , .
. , , , , . . a) (, , ); ) ; ) ) . "" , .
BB84 [7], . . [8]
H , QBER .
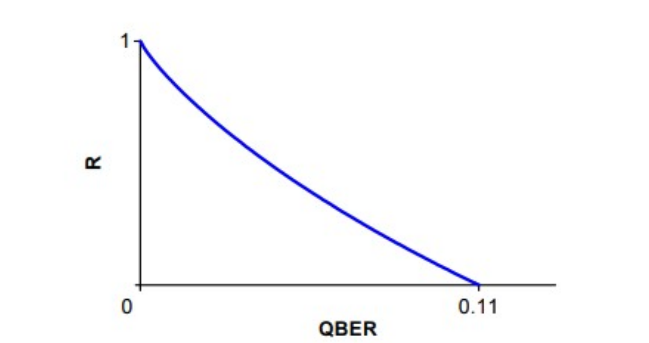
, . . , , . (, , ). , . PNS (photon number splitting)[2]. : , , . , , . , , [1].
2003 , BB84. , SARG04, BB84, . - -, [4]. , [4]. , , -. , . - . , PNS . Lo05[5]. - . ( - GLLP[3]) , . , ( .3).

SARG04[1]. : . ( !!!). , BB84, . , , :
.
( , ).
, , ( ). .
(
)
, ( ).
( 1/4), ,
(
,
,
). PNS : , 1 2 , 3 . [1].
, . SARG04 LPA(large pulse attack). , ( ). . , [6].
, . , . . , id Quantique [9], .4
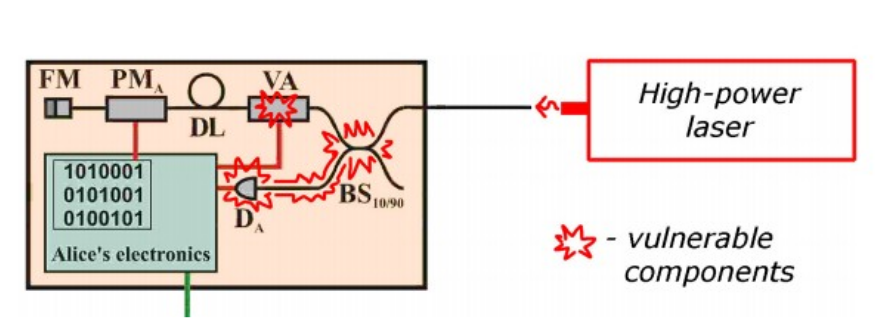
DA, , , . , . , , . ( ). : 1) ; 2) , ; 3) BS (, ); , , , , .
, , . . . . .
, ? : , , , . 1984 - , ? , , (RSA). , 1994 . , . , , .
:
1) A. Acin, N. Gisin, and V. Scarani, “Coherent-pulse implementations of quantum cryptography protocols resistant to photon-number-splitting attacks”
2) C. Bennett, F. Bessette, G. Brassard, L. Salvail, and J. Smolin, “Experimental quantum cryptography”(1992)
3) D. Gottesman, H.-K. Lo, N. L ̈utkenhaus, and J. Preskill, Quant. Inf. Comp. 4, 325 (2004)
4) W.-Y. Hwang, “Quantum key distribution with high loss: toward global secure communication”
5) Lo H., Ma X., Chen K. , “Decoy state quantum key distribution”, (2005)
6) Vadim Makarov, “Quantum cryptography and quantum cryptanalysis ”, (2006)
7) D. Mayers, “Quantum key distribution and string oblivious transfer in noisy channels” (1996); D. Mayers, “Unconditional security in quantum cryptography” (2001).
8) P. Shor and J. Preskill, “Simple proof of security of the BB84 quantum key distribution protocol” (2000).
9) D. Stucki, N. Gisin, O. Guinnard, G. Ribordy, and H. Zbinden, “Quantum key distribution over 67 km with a plug & play system”
10) Xiaoqing Tan, “Introduction to Quantum cryptography”, (2013)