NaN may still surprise you a little

At first, I thought this was just another question that might be asked in an interview. Probably, if you use your brains properly, you can guess what the result will be. Leaning back in his chair, he began to think, to turn on logic, to remember something on which to rely in reasoning. But in vain! Suddenly it became quite obvious that the answer could not be found. But why? What do you need to understand to find it? In mathematics? In a programming language?



The answer should be NaN. But why am I not sure about this? All the way, I was confident that any expressions containing NaN would return NaN. Well, perhaps only if you divide NaN by zero - in this case, a ZeroDivisionError exception will be thrown . One hundred percent NaN!



I enter the expression into a cell of notepad:

>>> 1**nan + 1**nan
2.0

Indeed? Wait:

>>> arange(5)**nan
array([nan,  1., nan, nan, nan])

That is, for some reason, one to the NaN power is one, but zero and all other numbers to the NaN power are NaN. Where is the logic? What's the matter?



So let's go again:

>>> 0**nan, 1**nan
(nan, 1.0)

Maybe I was just because of the lack of some practical need for deep knowledge about NaN, I just did not suspect something? Or maybe I knew, but forgot? Or maybe even worse - I didn't know and forgot?



We go to Wikipedia . There, this issue is also designated as a problem, but why everything is arranged this way is not explained in any way. But I learned that:

>>> hypot(inf, nan)
inf

Although, at the same time:

>>> sqrt(inf**2 + nan**2)
nan

That, you see, is also a little strange.



Okay, from Wikipedia we go to C99 on page 182 and finally get a logical explanation why pow (x, 0) returns 1 for any x , even for x equal to NaN:

>>> power(nan, 0)
1.0

If the function $$$f(x)$ is raised to the power $$$g(x)$ and wherein $$$g(x)$ tends to 0, then the result will be 1, regardless of what value is $$$f(x)$...







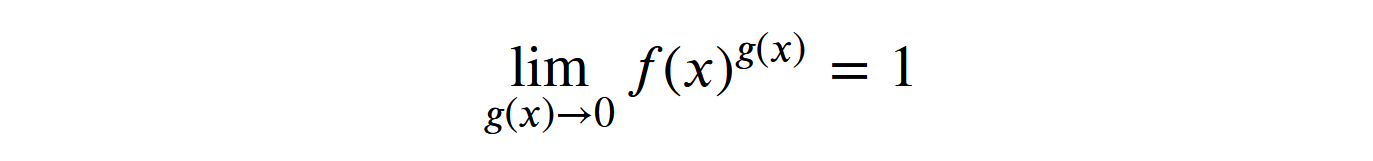
And if the result does not depend on the numerical value of the function$$$f(x)$, then 1 is a valid result, even for NaN. However, this still does not explain why 1 to the NaN power is 1. We



look for another C99 and on page 461 we see no explanation, just the requirement that pow (+1, y) must return 1 for all y , even equal NaN. Everything.



On the other hand, explaining why pow (NaN, 0) = 1 is preferable to pow (NaN, 0) = NaN still suggests that NaN should not be taken literally as Not-a-Number ... Suppose, as a result of some calculations, we got a number that exceeds the memory size allocated for this type of numbers, for example:

>>> a = pi*10e307
>>> a
inf

As a result, we got inf , what exactly this number we do not know, but still it is some kind of number. Then we calculated something again and again got too large a number:

>>> b = e*10e307
>>> b
inf

The difference between a and b will return NaN:

>>> c = a - b
>>> c
nan

The only reason we can count c as not a number is because we weren't using precise enough calculations. However, in c, underneath NaN there is some meaning hidden. We do not know what this meaning is. But it is still a number, and since this is a number, then there is nothing surprising in the fact that pow (1, NaN) = 1 .



Why then pow (0, NaN) = NaN ? The fact is that if we raise 0 to any power, then we really get zero. Except for one single case - when the degree is 0:

>>> 0**0
1

Because of this, in the expression pow (0, NaN) there is an ambiguity with a specific value of NaN. Of course, the probability that 0 can be hidden under NaN is vanishingly small, and one could assume that pow (0, NaN) = 0 . But nevertheless, it is better to play it safe, you never know what this can lead to. Perhaps that is how they reasoned when the standards were created.



I don't even know what else to say ... if you knew the answer in advance, then most likely you can be envied, because the areas where such knowledge can come in handy are probably full of interesting tasks. And maybe vice versa. Write about it in the comments.



PS Since NaN refers to floating point numbers, it can be a dictionary key:

>>> d = {0.1: 'a', nan: 'b'}
>>> d[nan]
'b'

Does it make sense to use this in practice? I don't think it's worth it.