🧒🏻 🧑🏿‍🤝‍🧑🏻 🚵🏻 Is there parallelism in an arbitrary algorithm and how to use it in the best way 🧔🏿 🏰 🤴🏿

Parallelization of data processing is currently used mainly to reduce computational time by simultaneously processing data in parts on many different computing devices, and then combining the results. Parallel execution makes it possible to “bypass” the fundamental law formulated by Lord Rayleigh in 1871, according to which (as applied to the heat dissipation of processors) their heat dissipation power is proportional to the fourth power of the processor clock frequency (doubling the frequency increases the heat dissipation 16 times) and actually replace it with a linear one from the number of parallel computers - while maintaining the clock frequency). Nothing is given for free - the problem of revealing (usually hidden for the uninitiated observer, [1]) the potential of parallelism in algorithms is not lying on the surface,and the effectiveness of its (parallelism) use - even more so.

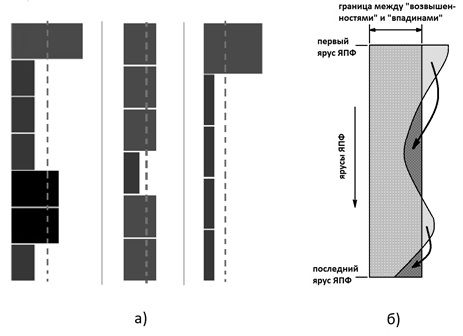
Below is an illustration of the parallelism detection process for the simplest case of evaluating the expression axb + a / c (a, b, c - input data).

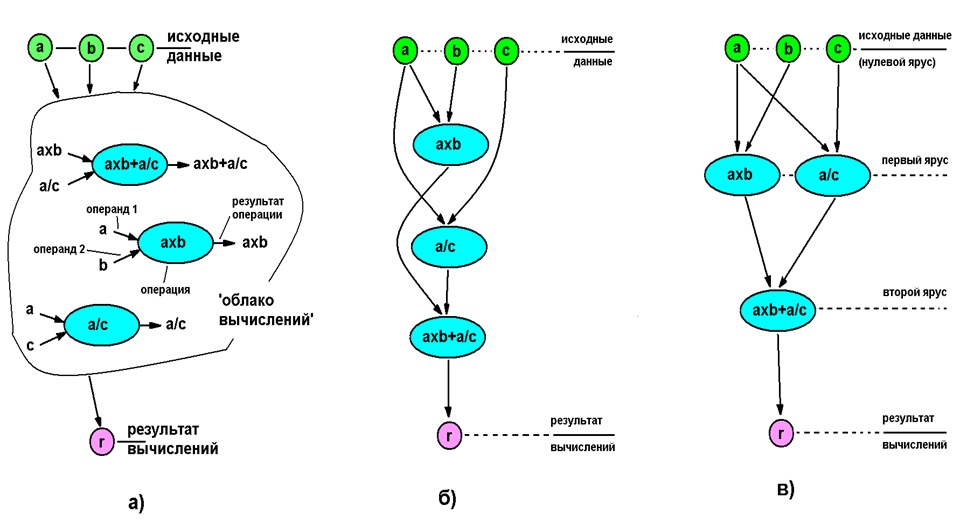
a) - "operator cloud" (sequence of execution is not defined), b) - completely sequential execution, not defined), b) - completely sequential execution, c) - parallel execution

, . ( ) ( – ., ). .1 “ ”, ( ) .

(- ), . , . () . NP- [2], ( ) ( -). , “ ” (Data Science).

AlgoWiki [3].

, , c ILP (Instruction-Level Parallelism, , EPIC (Explicitly Parallel Instruction Computing, ). , .

() ( , ). (). “ - ”, ( ) , – () ). , (- ).

( ) - (), [4]. ( ).

( ) O(N2) , N – ( ), ( ) . ( ). .. , . , .

, , .

. ax2+bx+c=0.

The figure shows the tier-parallel form of the algorithm for solving the complete quadratic equation in real numbers in the canonical form (the numbers of the tiers of the LPF are located on the right) — - - ( )

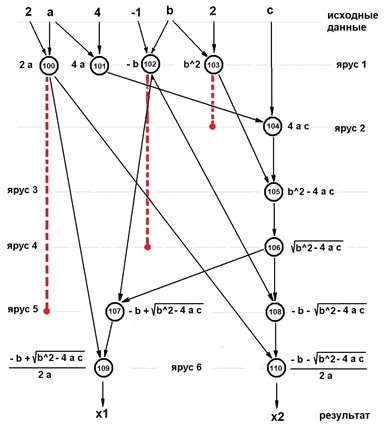
( “ ”, 6 4- ). ( ) – 1- 4, 2,3,4 - 5- 6 . , ( ) ( ) ! – ( ).

( ) , - D-F SPF@home. http://vbakanov.ru/dataflow/content/installdf.exe http://vbakanov.ru/spf@home/content/installspf.exe ( - http://vbakanov.ru/dataflow/dataflow.htm http://vbakanov.ru/spf@home/spf@home.htm).

The figure shows the diagram of the instrumental complex (* .set and * .gv - the program file and the file of the information graph of the analyzed program, respectively, * .mvr, * .med - files of the metrics of the vertices and arcs of the algorithm graph, respectively, * .cls, * .ops - files of parameters of calculators and program operators, respectively, * .lua - a text file in Lua language, containing methods of reorganization — - (*.set *.gv – , *.mvr, *.med – , *.cls, *.ops – , *.lua – Lua,

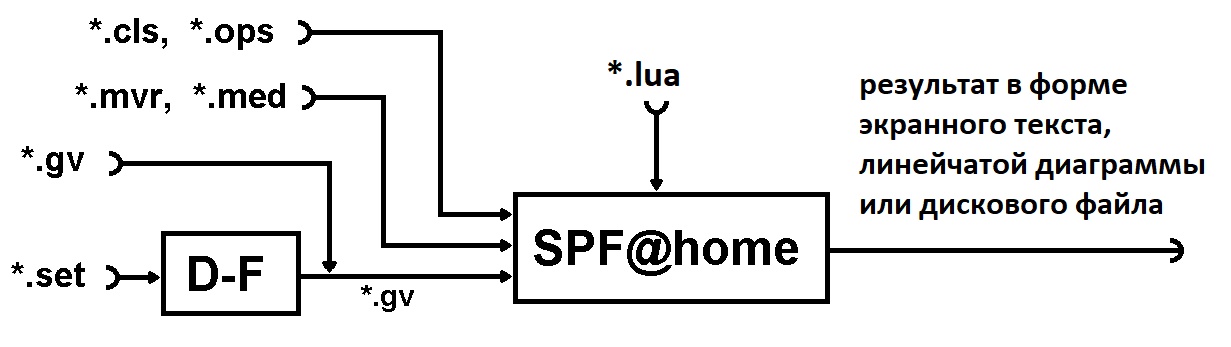
(set-) – gv- ( “ - ”, ( ) , – () ). , (- ).

() . “” .

Lua (Lua ANSI C, , - , ).

++, GUI Win’32- ( ) GIT-. ( ).

(Lua- “” API- SPF@home).

( D-F SPF@home ).

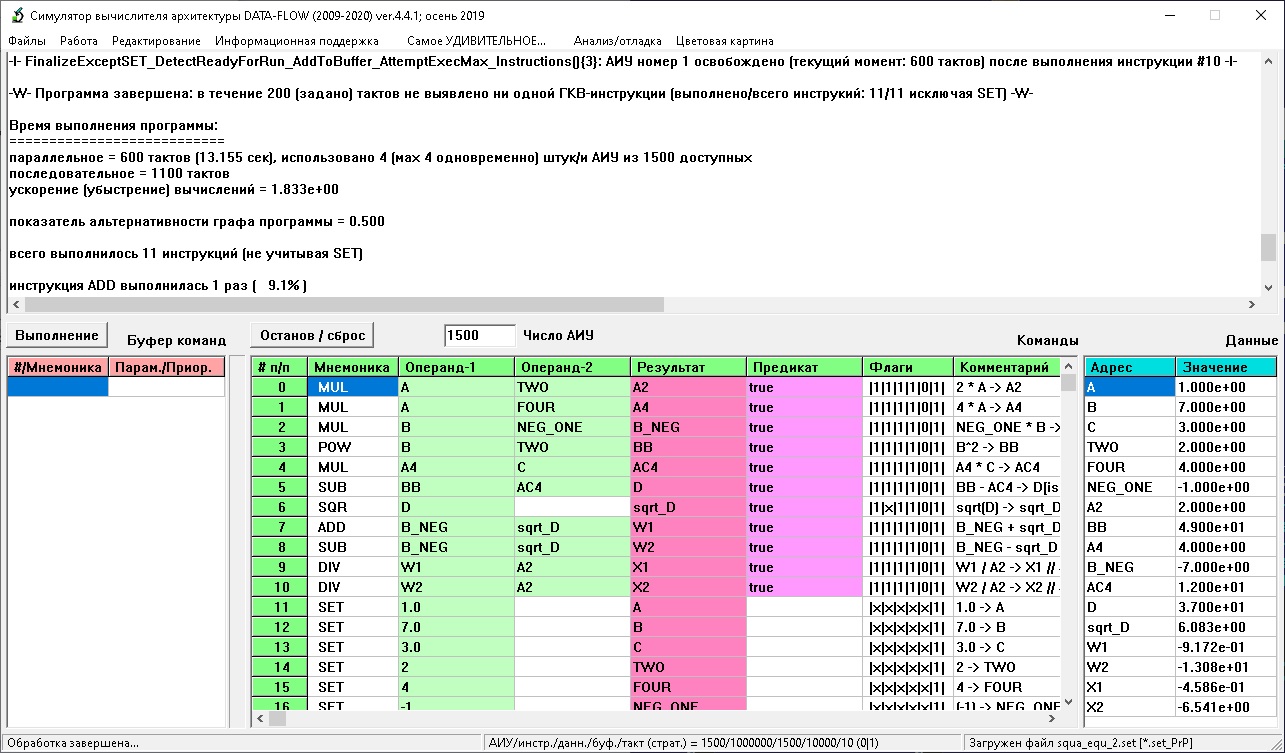
D-F (Data-Flow) , . 1 “Data-Flow” ( ), (), ; . - , , , “” . D-F , .

D-F , , . ( set- D-F, ):

, . D-F , - SPF@home. SPF@home gv- ( ), , Lua- ( API- , ):

CreateTiersByEdges("EdgesData.gv")  --     EdgesData.gv 
--    “”
-- CreateTiersByEdges_Bottom("EdgesData.gv")  --     EdgesData.gv 
--    “”
--
OpsOnTiers={} --   1D- OpsOnTiers 
for iTier=1,GetCountTiers() do --   
   OpsOnTiers[iTier]={} --  iTier-  2D- OpsOnTiers
   for nOp=1,GetCountOpsOnTier(iTier) do --       iTier  
      OpsOnTiers[iTier][nOp]=GetOpByNumbOnTier(nOp,iTier) --    nOp
end end --   for  iTier  for  nOp

gv- mvr med-, cls ops- . ( “-”, ) . , .

SPF@home “ ” , / ( ). med-.

, c ILP (Instruction-Level Parallelism, ), SPF@home .

.. Lua-, . ( ) :

I. “” ( ).

II. ( ).

III. .

( ) ; ( ).

, (, ) , , ( – ).

1) ( ) .

2) .

- . ( , , , ). “” API- “” ( , ).

“” ( ) ( ). “” “” ( ; “” ””).

( ) - “ ”, , “” . ( ). “” Windows- WinExec, ShellExecute CreateProcess, (, METIS -), Lua.

.6 ( ) “Bulldozer”, , “” “”.

In fig. shown are bar diagrams of the widths of the tiers of real IPFs from screen copies when the SPF @ home system is operating (the arithmetic mean of the widths is shown by a dotted line, a) and the symbolic scheme of the “Bulldozer” method - b) — . SPF@home (- , a) “Bulldozer” - )

, ( 1,5-2 ) , (- ).

.. ( Lua) (., c , , .).

SPF@home ( ) . , . ( ) ( , , ). , .

, ( ) .

1. .., .. . — .: -, 2002. — 608 c.
2. ., . . : — , , 2012. — 420 c.
3. AlgoWiki. . URL: http://algowiki-project.org ( 31.07.2020).
4. .. . . — .: -, 2018. — 390 .
5. Roberto Ierusalimschy. Programming in Lua. Third Edition. PUC-Rio, Brasil, Rio de Janeiro, 2013. — 348 p.

Is there parallelism in an arbitrary algorithm and how to use it in the best way

More articles: