In the first part, we looked at external algebra and realized that normal vectors in 3D can be interpreted as bivectors. To transform bivectors, in the general case, you need a matrix different from the one that transforms ordinary vectors. Using the canonical basis for bivectors, we found out that this is the adjoint matrix , which is proportional to the inverse transpose. This reasoning at least partially explained why the normals are transformed by the inverse transposed matrix.
But some issues were swept under the carpet.
We considered adjoint matrices, but did not show how they relate to the algebraic proof that for transforming the plane equationan inverse transposed matrix is needed. The proportionality between the matrices was, in a sense, far-fetched.
Moreover, we saw that -vectors from external algebra provide vector geometric objects with a natural interpretation, in which they contain units of length, area and volume, which change accordingly when scaled. But we did not find anything like this for densities - units inverse to length, area and volume.
In this article, we will look at another geometric concept that will be needed to complete the painting. Merging this new concept with the outer algebra already studied will clarify and resolve the remaining questions.
Functions as vectors
, . , , , .
: , ,
. — , … , ? ?
, . , (). , , : ( ). .
! . , : . , , .
: ( , ) — . . , , "". .
. , .
, .
, , . , .
( : , . !)
(3D) (2D), / , . :
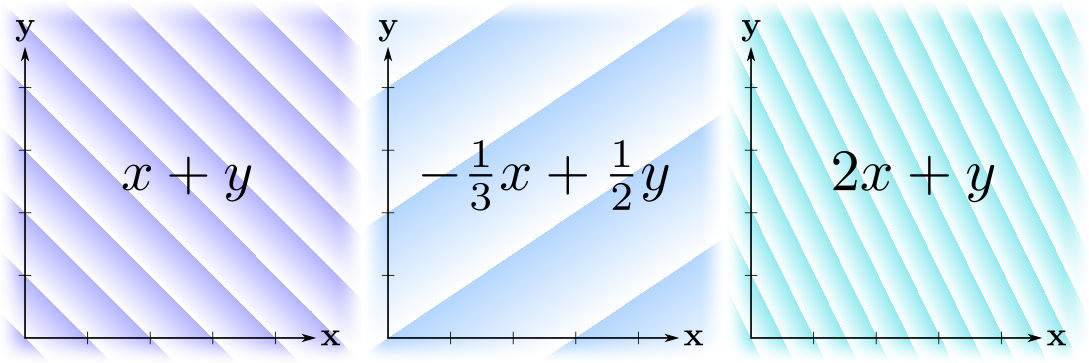
— . . , "́" ( ́ ) , .
, . , .
— — , : ( ) . . ( ) .
, — , , . - , , . , , .
, . . , — — , :
, — !
, : . .
, , , . , , "" . , — , … .
: . — , — . , . , — , .
:
, " " , .
. , , . :
. :
.
, , , . , . , . .
:
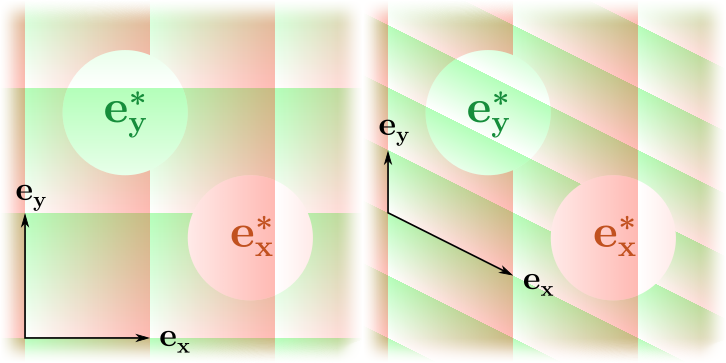
:
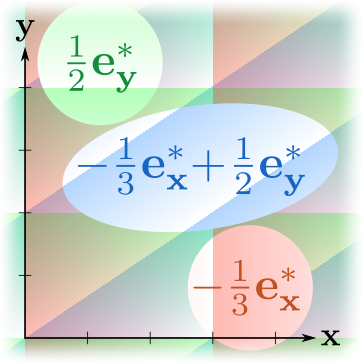
. :
, ( ), , , .
! "" ( ), ( 3D), ( ). !
— , . ?
: . , . : - . ( , ).
: , , . :
, , .
, . " " : .
, , . , . .
, . , ?
, , . , :
! , . "" "" . , , !
, . , (, , , //) - . ( ), " "" ?"
"". , , - , . .
. , , — , . .
. , :
:

? : .
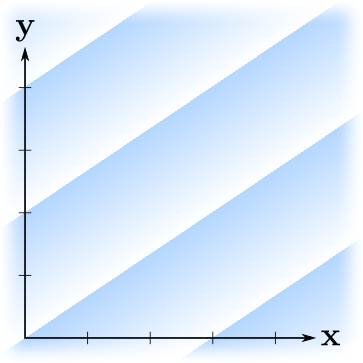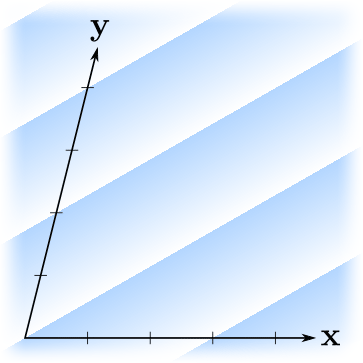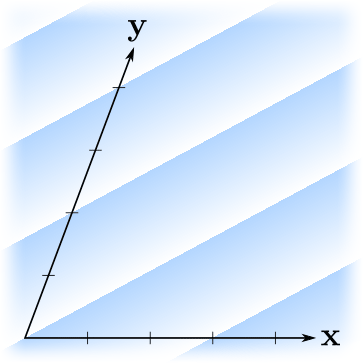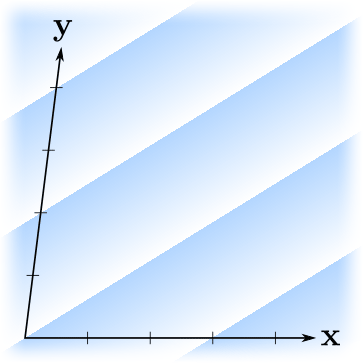
, ? . , — . ?
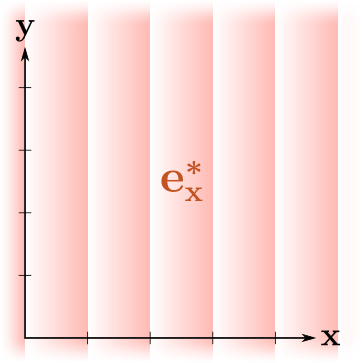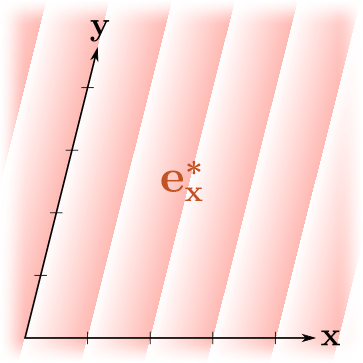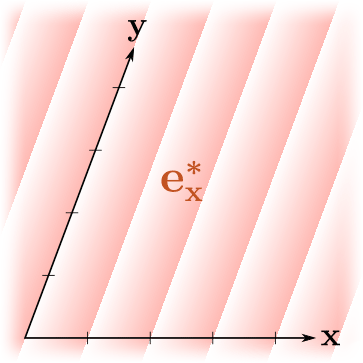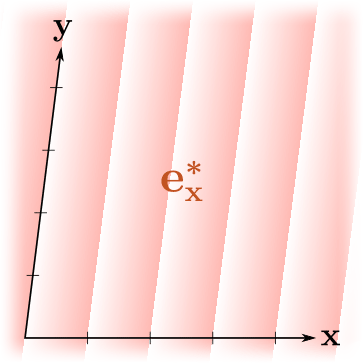
, ! , , , "" , . , .
, . , , , ,
!
, , . , , ( ), . :
.
, , .
?
, — 2D 3D. , , :
.
, , . :
, .
, , .
. , , , ? ?
, . " " , , . , : , . : , — .
This is all that I wanted to tell you about transformations of normal vectors, but a few more questions remain in limbo. At the end of the first part, I asked a question about negative degrees of scale. Now we have minus the first degree, but what about -2 and -3? To understand this, we have to combine outer algebra and dual spaces, which we will do in the third part.