
Probably, everyone was faced with the fact that they had to face some difficult task, the solution to which could not be found, not just right away - but even after long stubborn hours of work or days. Today we will talk about one of the classes of such problems - NP-complete.
In general, is it realistic to meet such tasks in everyday life? In fact, they arise in a huge number of cases: combinatorics, graphs and networks, execution of logical formulas, working with maps, optimal loadings, maps, discrete optimization problems, finding the longest sequences, finding equal sums, and many set problems! And this is not a complete list.
Under the cut is an informal guide - how to understand that you may have an NP problem in front of you and what to do if this is exactly what it turned out to be. Today we are attacking this issue from the practical side.
Make sure that she really is in front of you
How do you know when you are faced with an NP-complete problem? First, the simplest detection heuristic is a search through already known NP-complete problems in order to determine something similar, there are many such lists, for example .
Second, consider the following properties of tasks:
- We need to choose a solution in which n elements from the space exp (n)
- If you already have a solution of length n from this space, it can be easily (polynomially) checked
- The choice of one of the decision elements (may) affects the choice of all the others (not necessarily all).
- In the worst case, the options can always be enumerated, considering the entire exponential space by a simple enumeration.
- The parameters n - the length of the solution or the space itself do not have a fixed value, that is, we are not talking about the always fixed 8 by 8 chessboard, but about the general form of the N-by-N problem.
Read more about the properties of NP-complete problems here and here .
An example of work on this list
Let's give a simple example on a problem that was recently approved as NP-complete!
Based on the materials of the article. You need to place N queens on a board of size N by N, provided that already K <= N are placed on the board (picture from the original scientific article)
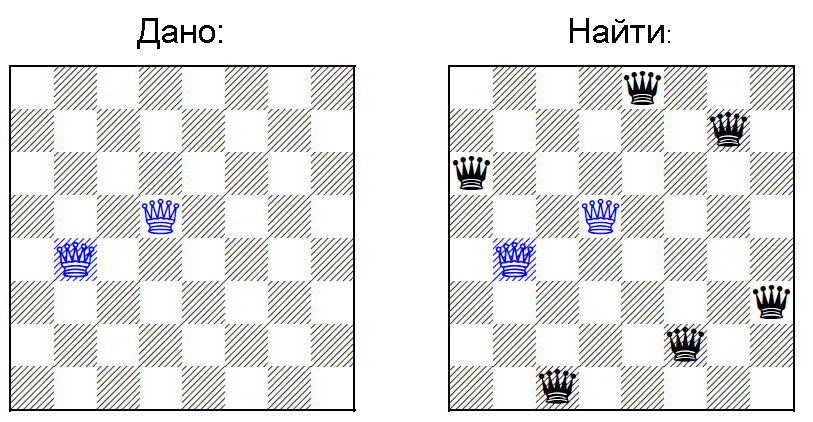
First, note that a very similar problem with partially constrained Latin squares NP is complete.
And then we go through the list:
- You need to find N queens on from the space exp (N) (= N ^ 2 * (N ^ 2-1) * ....).
- The solution of N queens is trivially checked - for each queen, you need to check the diagonals, verticals and horizontal lines.
- Setting one makes the choice of a number of others invalid - i.e. there are dependencies between the elements of the solution (you cannot arrange queens independently).
- Here you can solve the problem by brute force for an arbitrarily chosen board in exp (N) - we put the first one in the first one on the (i, j) position, the second one on any other unoccupied one, and so on. Backtracking is guaranteed to find a solution.
- The problem has no fixed parameters - that is, it is formulated in a general form and as N grows, so does the complexity.
Note that one of the items in the list fails if the board is always known to be clean and the task becomes trivial.
Moreover, it is a conditional practical approach - a heuristic for detecting NP-complete problems (with all the pros and cons).
Mixing
Source
Why, having on hand similar problems, it is not easy to understand formally that we have an NP-problem? We really need to shine an NP problem to ours, then we will know for sure that our problem is NP-hard! And if we were able to simulate it, as in the list above, then it is complete - that is, at least NP and no more than NP, in fact “the most difficult among NP problems” (like the rest of the NP-complete ones).
Okay, do we need it? Not really, if you are straightforward, after all the checks, that you are dealing with an NP-problem, then you do not need to prove anything unless you are writing a scientific article.
And you need either (we'll talk about this below):
- simulate your task using systems that solve such tasks;
- find a solution that works fast enough in your case;
- find an approximate solution that will satisfy us.
Don't give up!
The most important thing is to evaluate dimensions-parameters and realistic scenarios!
xkcd.com/287
For example, you know that despite the fact that the values of the parameters are not fixed, the conditional N <100 is not implemented in all practical scenarios, which means that conditional enumeration may be a real solution for you.
You need to determine for yourself: what real values of the parameters are possible and really come into the system, what is the general distribution and features of the data, what is real and what is not? Do we need the most optimal solution? Let's go through these points.
Distribution of input data
Or despite the fact that in the general case the input data can be any, but again using the example of queens - usually one queen or even none is fixed. This means that 90% of the time you can use a very simple solution and only call a complex one in extreme cases.
An example when, on average, all the usual combinations are simple: the problem of complementing queens - we know that conditional DFS + heuristics can in most cases find solutions very quickly, and only in very non-standard situations can be extremely difficult.

Here is an example of how the solution for a very specialized NP-complete tiling problem was evaluated against a general method for modeling a whole class of such problems using logic programming methods:
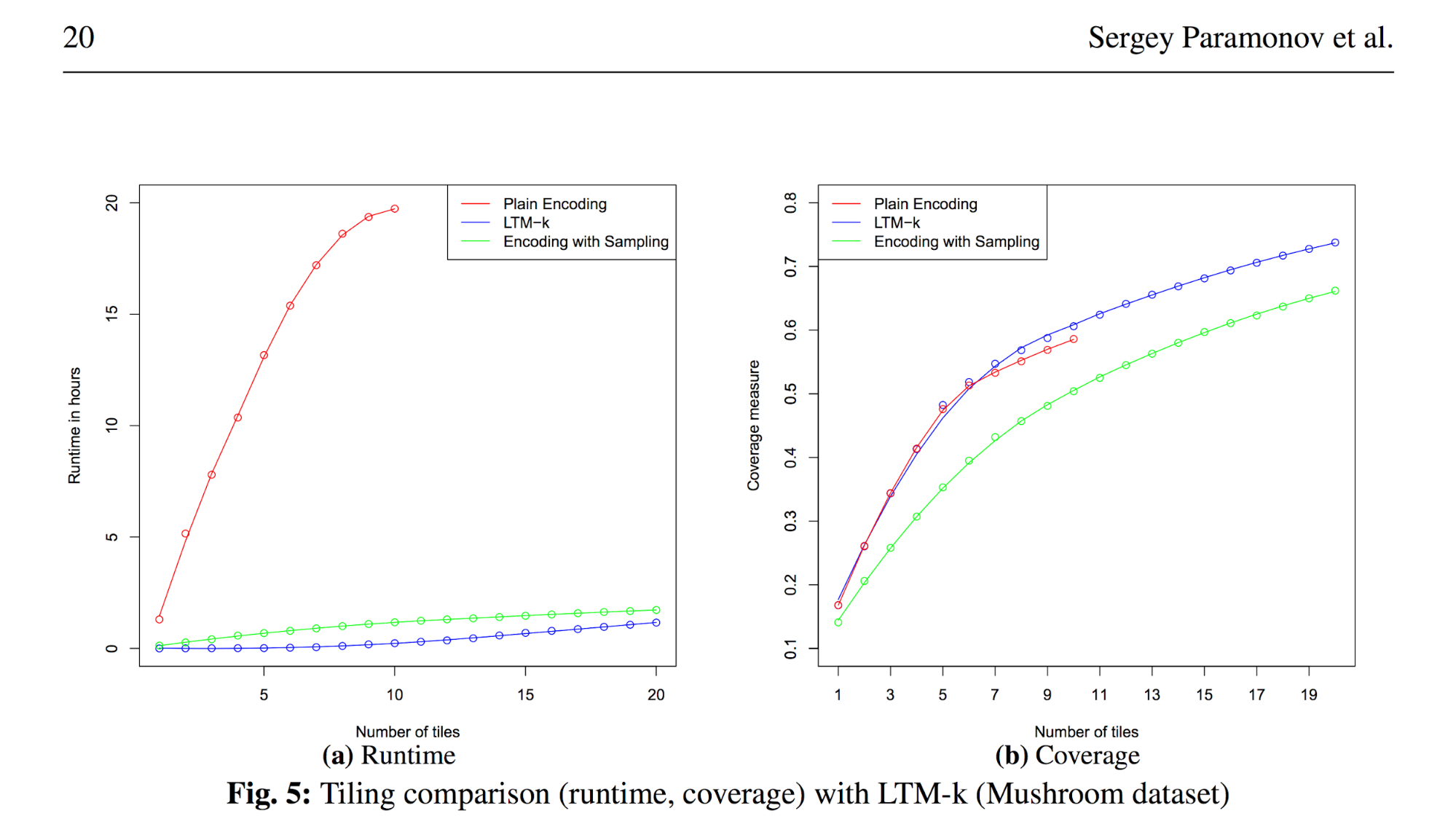
(from the article Relational Data Factorization (Paramonov, Sergey; van Leeuwen, Matthijs; De Raedt, Luc: Relational data factorization, Machine Learning, volume 106))
First, the speed of the special LTM-k solution and the general method is significantly different. Thus, a heuristic-based solution for just this type of problem can completely solve this problem.
Second, by sacrificing the quality of the solution, the general approximation method gave a very similar speed.
Heuristics and approximation
The last and most powerful tool is to use NP-complete problem modeling systems such as Answer Set Programming .
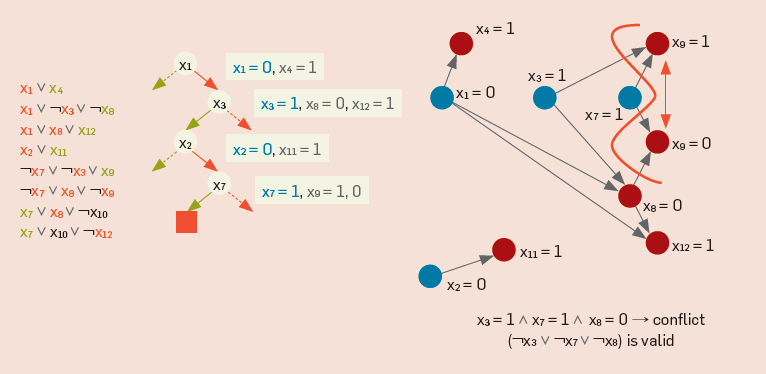
More about logical programming languages.
For example, the solution to the queen placement problem will look like this:
% domain
row(1..n).
column(1..n).
% alldifferent: guess a solution
1 { queen(X,Y) : column(Y) } 1 :- row(X).
1 { queen(X,Y) : row(X) } 1 :- column(Y).
% remove conflicting answers: check this solution
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 == Y2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 + X1 == Y2 + X2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 - X1 == Y2 - X2.
Having carried out a simple experiment to find solutions for a different number of queens N, we get the following: along the X axis - queens, along Y - the time per second to find a solution:
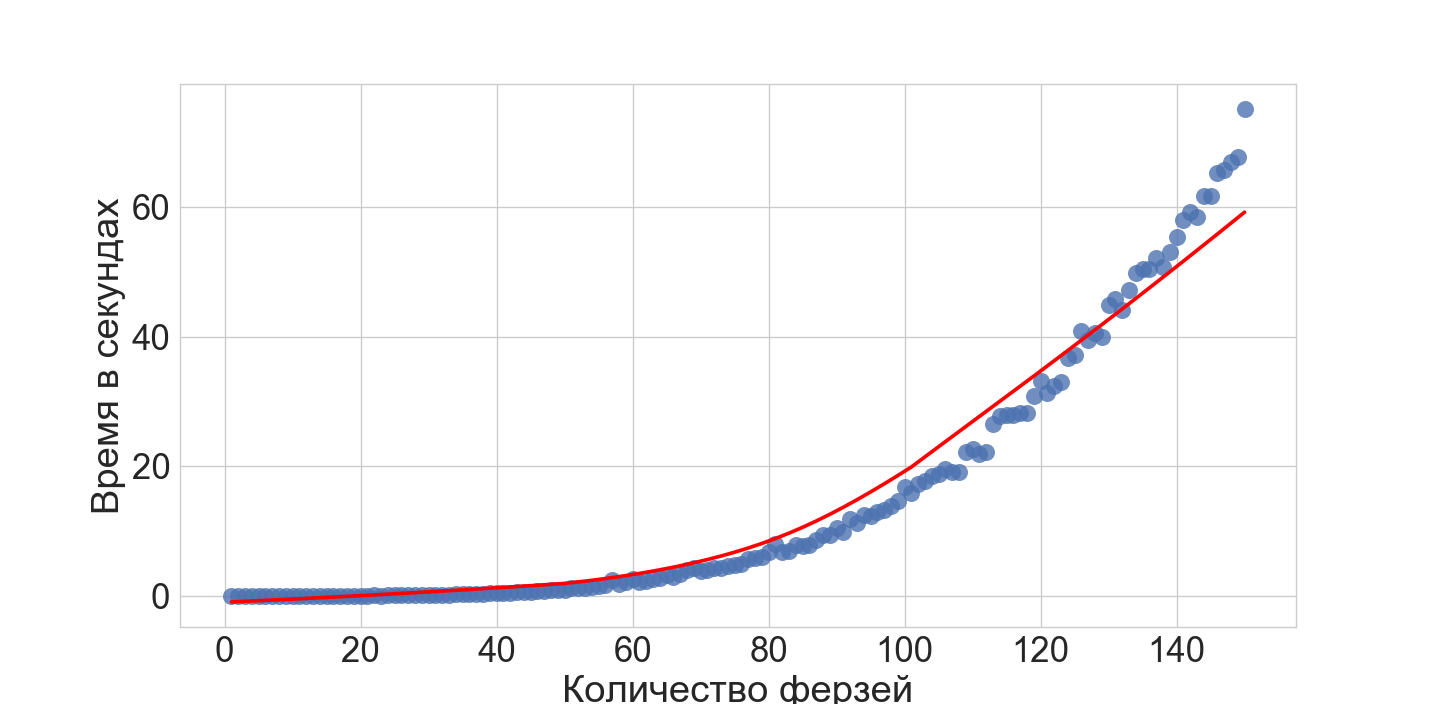
We see that despite the fact that the growth of time is clearly not polynomial (which is logical), we do a good job with an adequate number of queens and board sizes.
Then, if we know what board dimensions are real for us, we can understand how this exact solution is acceptable for us in a real system.
conclusions
Let's go over the ideas from the article in the form of a checklist
- Determine that you really have an NP problem.
- Understand what realistic parameter values and data distribution are.
- Try to write (the order depends on the developer and / or task):
- An accurate heuristic solution (based on our analysis) - will it be fast enough?
- — ?
- NP- — ? , CPU ? .
- : , .
- — , — . !
:

