There is such a mysterious fact about linear transformations: some of them, namely non-uniform scaling and translation, for some reason distinguish between "ordinary" vectors and normals. When we transform a "normal" vector by a matrix, then the normals for some reason need to be transformed by an inverse transposed matrix. How to understand this?

With the help of simple calculations, you can make sure that the inverse transposed matrix preserves the perpendicularity of the normals to its tangent planes. To some extent, this proof is sufficient, but it misses a deeper and more interesting story about the geometry behind it all. This is the story I want to tell in the next few articles.

Units and scaling

Here's a quick rundown before we dig into the heart of the article. Consider good old uniform scaling (one factor across all axes). It's hard to think of a more innocuous transformation - it's just the multiplication of all vectors by the same number.

But upon closer inspection, something not entirely trivial is happening here. Certain quantities carry with them physical "dimensions" or "units" such as lengths, areas, and volumes. When scaling, these values ​​change in accordance with their units. Some values ​​are generally "dimensionless" and do not change when scaled.

As an example, let's list all the possible behavior of units when scaling in three-dimensional space. We denote the scale factor as$$$a>0$... Then:

• Dimensionless numbers do not change, in other words, they are multiplied by$$$a^0$...
• The lengths are multiplied by$$$a$...
• Areas are multiplied by$$$a^2$...
• Volumes are multiplied by$$$a^3$.
  
  : , :
• $$$1\over{a}$.
• $$$1\over{a^2}$.
• $$$1\over{a^3}$.
  
  , , . 3D- , , , .

, ( ) , : , ( ), , - . , -3 3. , $$$k$- , $$$a^k$.

( $$$\pm 4$ , . , 3D.)

, - . ? ? ? -, .

, . , . , Geometric Algebra for Computer Science. .

— , , , , . $$$k$-, $$$k$ — . , — . .

— ( ) , . , , . , .

, , . , . , . , , , .



, — , , . , , , , .

. , , . , , "" "", "" "". , , .

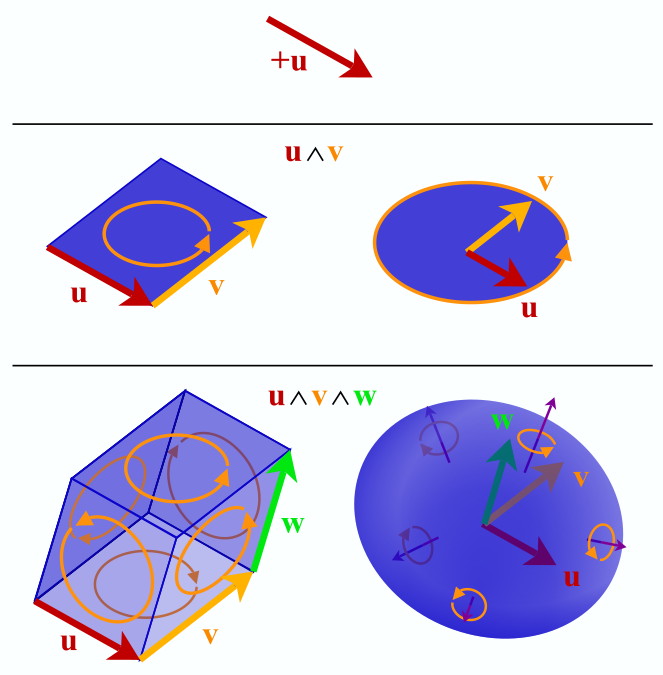
́ , . , $$$k$- . .

$$$k$-

, . $$$v=(x, y, z)$, , $$$v$ :

$$

$$v=x{\bf e_x}+y{\bf e_y}+z{\bf e_z}$$

$$${\bf e_x}$, $$${\bf e_y}$, $$${\bf e_z}$ $$, $$$y$, $$$z$. $$$B$ :

$$

$$B=p{\bf e_{yz}}+q{\bf e_{zx}}+r{\bf e_{xy}}$$

$$${\bf e_{xy}}$ — , $$$xy$. $$${\bf e_{yz}}$ $$${\bf e_{zx}}$ . , , . " " $$$(p, q, r)$, .



:

$$

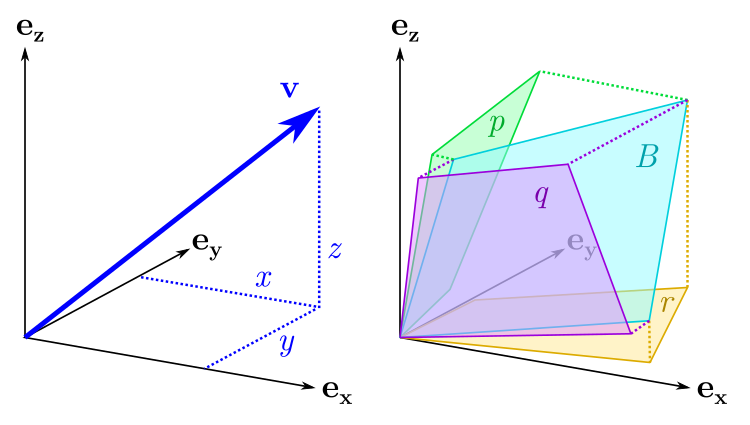
$$T=t{\bf e_{xyz}}$$

, 3D , : "" $$$(xyz)$. — $$${\bf e_{xyz}}$ .

, : ( 1), ( 2) ( 3). 0. , , , $$$\wedge$. , , :

$$

$${\bf e_x}\wedge{\bf e_y} = {\bf e_{xy}}$$

, , . , ( ).

, "" . , , . , .

, , .

$$

$${\bf e_x}\wedge{\bf e_y}\wedge{\bf e_z} = {\bf e_{xy}}\wedge{\bf e_z}={\bf e_{xyz}}$$

" ", , , .

, . . $$$a$ :

$$

$$(au)\wedge v=u\wedge (av) = a(u\wedge v)$$

, . $$$u, v$ :

$$

$$u\wedge v=-(v\wedge u)$$

. -, : $$$v\wedge v=0$. , . , $$$u\wedge v=0$ $$$u$ $$$v$ . , $$$u\wedge v\wedge w=0$ $$$u, v, w$ .

3 . , .

$$$k$-

, , — , — . ?

, , - . $$$a>0$ , $$$a, a^2, a^3$ . , , .

, :

$$

$$v\mapsto Mv$$

$$

$$\begin{bmatrix} x \\ y \\ z \end{bmatrix} \mapsto \begin{bmatrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} ax \\ ay \\. az \end{bmatrix} = av$$

$$$v$ , $$$x, y, z$, , $$$a$ , , .

? ( ), . . , , :

$$

$$\begin{aligned} B &= u \wedge v \\ (u \wedge v) &\mapsto (Mu) \wedge (Mv) \\ &= (au) \wedge (av) \\ &= a^2 (u \wedge v) \\ &= a^2 B \end{aligned}$$

! , $$$a$, $$$a^2$, .

, . , - $$$a^3$. :

$$

$$\begin{aligned} T &= (u \wedge v \wedge w) \\ (u \wedge v \wedge w) &\mapsto (Mu) \wedge (Mv) \wedge (Mw) \\ &= (au) \wedge (av) \wedge (aw) \\ &= a^3 (u \wedge v \wedge w) \\ &= a^3 T \end{aligned}$$

. , ?

, . 3 $$$x$, . :

$$

$$M = \begin{bmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

: $$$x$ 3, $$$y, z$ . , : , $$$x$ , $$$yz$ — .



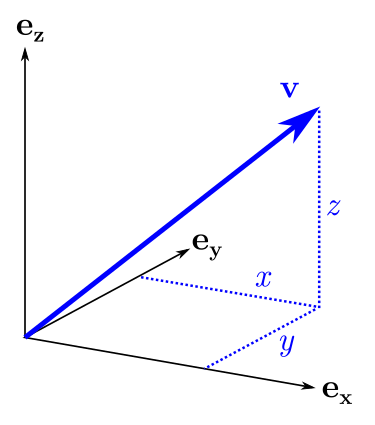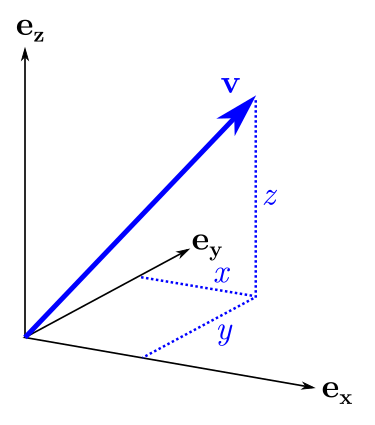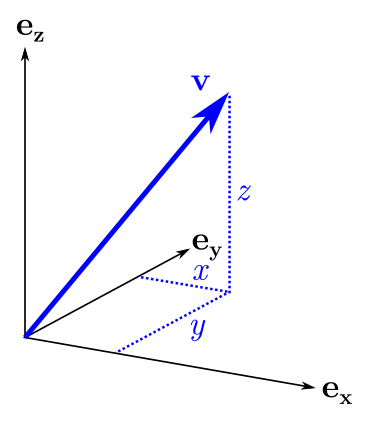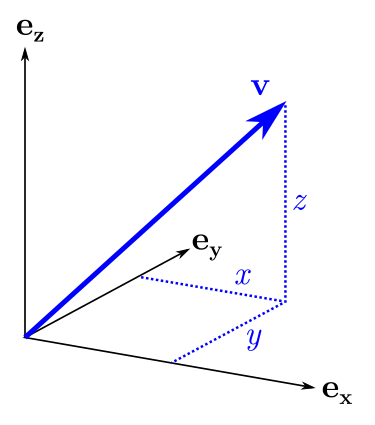
? . , "" . $$$x$ , . : , $$$yz$, , , $$$x$, .



, . , , :

$$

$$B = p \, {\bf e_{yz}} + q \, {\bf e_{zx}} + r \, {\bf e_{xy}}$$

$$$M$ , . $$$M$ :

$$

$$\begin{aligned} {\bf e_{yz}} = {\bf e_y} \wedge {\bf e_z} \quad &\mapsto \quad (M{\bf e_y}) \wedge (M{\bf e_z}) = {\bf e_y} \wedge {\bf e_z} = {\bf e_{yz}} \\ {\bf e_{zx}} = {\bf e_z} \wedge {\bf e_x} \quad &\mapsto \quad (M{\bf e_z}) \wedge (M{\bf e_x}) = {\bf e_z} \wedge 3{\bf e_x} = 3{\bf e_{zx}} \\ {\bf e_{xy}} = {\bf e_x} \wedge {\bf e_y} \quad &\mapsto \quad (M{\bf e_x}) \wedge (M{\bf e_y}) = 3{\bf e_x} \wedge {\bf e_y} = 3{\bf e_{xy}} \end{aligned}$$

: $$$\bf e_{yz}$ , $$$\bf e_{zx}$ $$$\bf e_{xy}$ 3, $$$x$.

, $$$M$ $$$B$:

$$

$$B \mapsto p \, {\bf e_{yz}} + 3q \, {\bf e_{zx}} + 3r \, {\bf e_{xy}}$$

, , $$$B$ , :

$$

$$\begin{bmatrix} p \\ q \\ r \end{bmatrix} \mapsto \begin{bmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix} p \\ q \\ r \end{bmatrix} = \begin{bmatrix} p \\ 3q \\ 3r \end{bmatrix}$$

, , . : $$$M$ .

: $$$M$ :

$$

$$M^{-T} = \begin{bmatrix} \tfrac{1}{3} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

?

, — $$$M$.

$$$\det M$. ( $$$M$ , $$$\det M$). $$$M$ . , , !

— , . .

$$$n\times n$ . $$$i$- $$$j$- :

1. $$$n\times n$ $$$i$ $$$j$. $$$(n-1)\times (n-1)$.
2. .
3. $$$(-1)^{i+j}$, $$$i+j$ . !

$$$n\times n$, .

, ? $$$p \, {\bf e_{yz}}$. $$$yz$, , $$$M$ $$$y$ $$$z$. $$$1,1$ $$$M$ $$$2\times2$, $$$M$ $$$y$ $$$z$. , , $$$yz$!

- , $$${\bf e_{yz}}, {\bf e_{zx}}, {\bf e_{xy}}$ , , $$$M$ . , , $$$M$ . , , .

( , . $$${\bf e_{xz}}$ $$${\bf e_{zx}}$. .)

, , $$$n$ $$$(n-1)$- . , $$$k$- $$$(n-k)$- , $$$n-k$ .

. . : 3D. , $$$(p, q, r)$ — $$$(x, y, z)$ !

. , . , $$$B$ :

$$

$$B\wedge v=0$$

$$$v$, $$$B$ , . , , , $$$B$ $$$v$ .

:

$$

$$\begin{gathered} (p \, {\bf e_{yz}} + q \, {\bf e_{zx}} + r \, {\bf e_{xy}}) \wedge (x \, {\bf e_x} + y \, {\bf e_y} + z \, {\bf e_z}) = 0 \\ (px \, {\bf e_{yzx}} + qy \, {\bf e_{zxy}} + rz \, {\bf e_{xyz}}) = 0 \\ (px + qy + rz) {\bf e_{xyz}} = 0 \\ px + qy + rz = 0 \\ \end{gathered}$$

. , , (, $$${\bf e_{yz}} \wedge {\bf e_y} = 0$). $$$\bf e_{xyz}$, , . . , $$$\bf e_{xyz}$ .

$$$(p, q, r)$ $$$(x, y, z)$! , $$$n\cdot v = 0$ $$$n=(p, q, r)$.

, $$$(p, q, r)$ $$${\bf e_{yz}}, {\bf e_{zx}}, {\bf e_{xy}}$ $$${\bf e_x}, {\bf e_y}, {\bf e_z}$. , . , . .

, - . — . ( ) " ".

, . , "" , . ? , , ? , , ( ). .

: , , -3 3. , $$$k$- $$$k$0 to 3. But what about vector units with negative degrees of scale? Do they exist? If so, what are they?

In the next episode, we will dig even deeper and complicate our geometric story even more.