What? What for?
Hello!
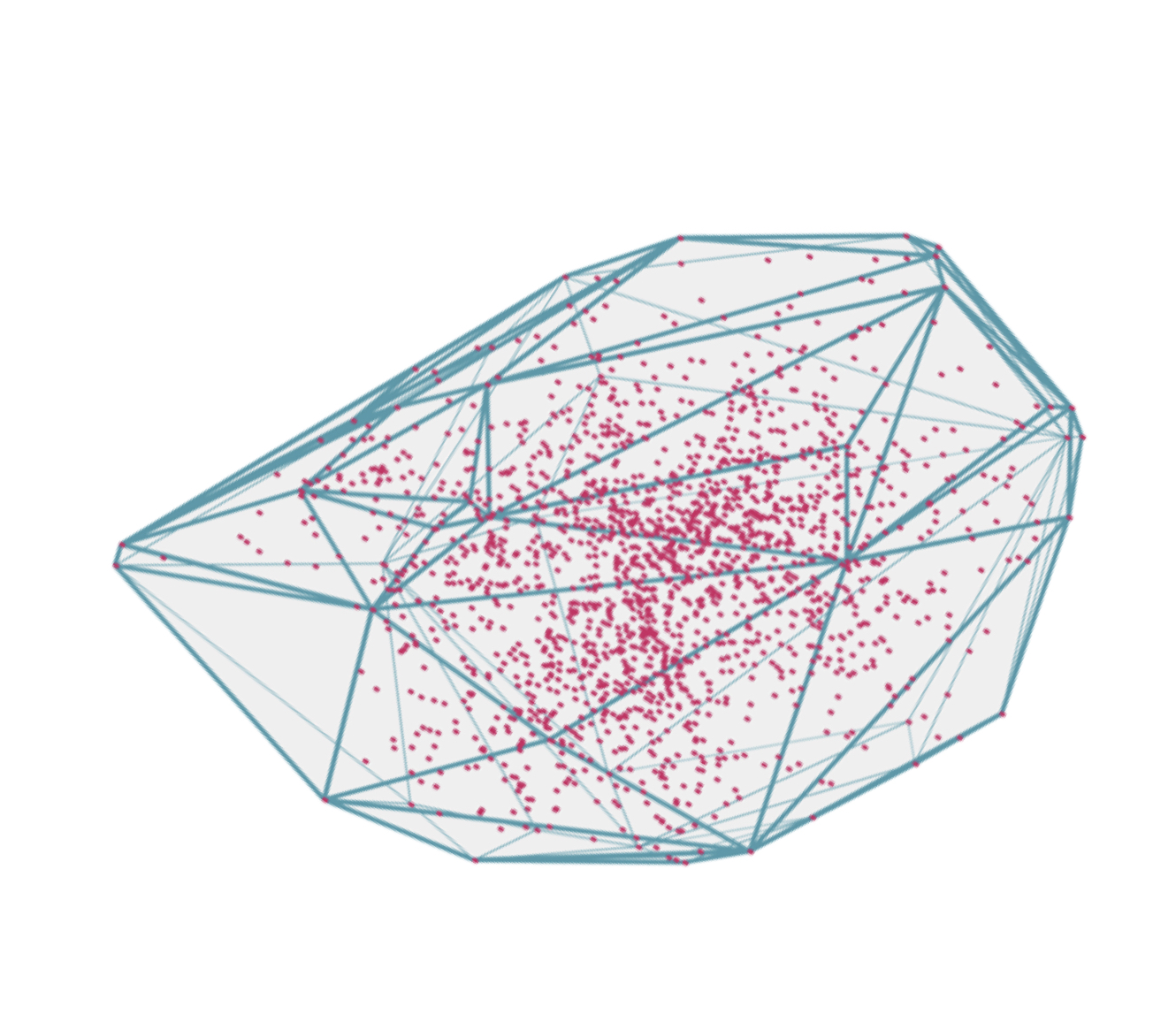
I would like to consider a computational geometry problem, namely building a convex 3D hull . As it seems to me, this is neither the most complicated nor the simplest algorithm that would be very interesting and useful to analyze.
If you have never faced such a task, I think it will be interesting for you to learn about it, see what it is.
If you have just heard something about convex hulls, you can find out more about them.
If you are a guru of convex hulls, you may like to listen to the solution to an interesting problem again.
Content
- What? What for?
- What is a Convex Hull?
- Common words
- Algorithm Description
- Asymptotics
- Algorithm implementation
- Full implementation
I express my gratitude muji-4ok for help in writing and editing the article.
What is a Convex Hull?
The convex hull of a set X is the smallest convex set containing the set X.
Strictly, but not very clear. Now I will try to tell you with an example:
Imagine a set of points on a plane, and let's say we want to know what is the minimum number of points that must be connected in order for the remaining set of points to lie inside the outlined surface. This is the problem of finding the minimal convex hull.

2D
,
, , , , , , "" , .
, , , 3D . , .
: , ?
— .
— . , , : .
, , .
, ( ) " ".
, 4 . 3 .
, , .
, , 3d , . , .
1.
, , , , .
, .
Z. , , "" Z . XY , . . , . P, , "" — f.
, . Q, f ( prQ). , () {P, Q} {Q, prQ} — — . , Q , . Q .

. R, , P, Q R (0, 0, 1) . , f — XY. , , . , , R .
, , , , ( - ).
, P, Q, R .
-! , .
2.
, , , . , .
: , . , , , , () ( ), , . , , , , .
: , . : .
1. ? , . . E. , , E — R. ( E) , E R. , , , — .
2. , , " ", E , , E .
3. , , . , , . , , , .
4. , . , . , "" , .
5. , "" , .
6. , . , .
, ( ), 3D .
, , . , . N, H , O(NH). H 2N, O(N^2).
, , , O(NlogN), , . 2D , O(NlogN), , , , .
, , : .
, , , , , . C++.
. . , , -. - . ( , ).
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point (coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator- (const Point& other) const;
Point operator+ (const Point& other) const;
bool operator!= (const Point& other) const;
bool operator== (const Point& other) const;
};. 22 ( ).
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}( A — — - - AB AC):
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}( ):
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}:
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}, .
. , . , , , , . , , .
struct Edge
{
int first;
int second;
int flatness; //
bool is_close = false; // , ?
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)) :
first(first), second(second), flatness(flatness) {}
};Flatness — . 3 , ( ). — Another, . ( — if — .)
struct Flatness
{
int first;
int second;
int third;
Point normal; // ,
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two);
};Class .
class ConvexHull
{
struct Flatness;
struct Edge;
std::vector<Point> points_; //
std::vector<Flatness> verge_; //
std::vector<Edge> edges_; //
int count_; //
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point>& points): points_(points), count_(points.size()) { makeHull(); }
};
: Z ( , )
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}, :
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}. (-)
. , : . - , , .
:
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point; //
first_point = findMinZ();, Z. "".
double min_angle = 7; // 2pi, 7
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i) //
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;, .
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;, , XY, (0, 0, 1). .
( ), .
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); //
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
} :
:
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);: , . , : .
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // ,
stack.pop();
if (e.is_close) // ,
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // ,
{
// , i-
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}, , e , . , , is_closed = true, , , , — — , .
if (min_id != -1) // - 4
{
e.is_close = true; // ,
int count_flatness = verge_.size(); //
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id); // -1,
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // while
} // #include <iostream>
#include <vector>
#include <cmath>
#include <stack>
#include <iomanip>
using coordinate = int64_t;
struct Point;
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22);
Point VectorProduct(const Point& A, const Point& B, const Point& C);
double GetLenghtVector(Point A, Point B);
double GetAngle(const Point& n1, const Point& n2);
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point(coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator-(const Point& other) const
{
return Point(x - other.x, y - other.y, z - other.z);
}
Point operator+(const Point& other) const
{
return Point(x + other.x, y + other.y, z + other.z);
}
bool operator!= (const Point& other) const
{
return (x != other.x || y != other.y || z != other.z);
}
bool operator== (const Point& other) const
{
return (x == other.x && y == other.y && z == other.z);
}
};
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}
//[AB, AC]
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}
//vector AB
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}
class ConvexHull
{
struct Flatness
{
int first;
int second;
int third;
Point normal; // ,
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two)
{
if ((one == first && two == second) || (one == second && two == first))
{
return third;
}
if ((one == first && two == third) || (one == third && two == first))
{
return second;
}
if ((one == third && two == second) || (one == second && two == third))
{
return first;
}
return -1; // error
}
};
struct Edge
{
int first;
int second;
int flatness; //
bool is_close = false;
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)):
first(first), second(second), flatness(flatness) {}
};
std::vector<Point> points_;
std::vector<Flatness> verge_;
std::vector<Edge> edges_;
int count_; //
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point>& points): points_(points), count_(points.size()) { makeHull();}
};
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // ,
stack.pop();
if (e.is_close) // ,
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // ,
{
// , i-
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}
if (min_id != -1) // - 4
{
e.is_close = true; // ,
int count_flatness = verge_.size(); //
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id);
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // while
} //
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point;
first_point = findMinZ();
double min_angle = 7;
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i)
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;
//
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); //
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
}
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}.