🍁 💿 🖤 Knapsack problem in cryptography 👨🏽‍⚕️ 🍩 🤾

The Knapsack Problem (Knapsack Problem) is the problem on which the American cryptographers Ralph Merkle and Martin Hellman developed the first public key encryption algorithm.

Further in the program

Formulation of the knapsack problem (+ why a knapsack?)
Easy and hard challenges
Examples of
History

What is public key encryption?

, , «», .

. , , , .

: , .

, - !

The first general public key algorithm used the knapsack algorithm.

Based on the definition of public key systems, it takes two keys to successfully encrypt (and decrypt) a message. The "legal" recipient of the message knows the secret key

$ inline $ A $ inline $

while the sender owns another public key

$ inline $ B $ inline $

...

What to do if a public key becomes known to an attacker?

There is an answer: the public key must be obtained from the secret key using a transformation ( one-way function )

$ inline $ f $ inline $

with the following two properties:

$$ inline $ B = f (A) $ inline $$ knowing A, it is easy to calculate the function itself

$$ inline $ A = f ^ {- 1} (B) $ inline $$ , and it is difficult to calculate the inverse function

What is "easy" and "difficult"?

.

«» , . ..

n

$n$ , —

t \propto n^{a}

$t \propto n^a$ ,

a

$a$ — . , .

«» . , , .

..

n

$n$ ,

t \propto 2 n

$t \propto 2n$ , , .

The knapsack problem is formulated as follows

The set (backpack vector)

$ inline $ A = (a_1, ..., a_n) $ inline $

Is an ordered set of

$ inline $ n $ inline $

(

$ inline $ n> 2), $ inline $

distinct natural numbers

$ inline $ a_i $ inline $

... Let there be a number

$ inline $ k $ inline $

- whole and positive. The task is to find such a set

$ inline $ a_i $ inline $

so that in total they give exactly

$ inline $ k $ inline $

...

In the most famous version of the knapsack problem, it is required to find out whether a given pair has

$ inline $ (A, k) $ inline $

decision. In the variant used in cryptography, you need for this input

$ inline $ (A, k) $ inline $

build a solution knowing that such a solution exists. Both of these options are NP-complete.

Backpack analogy

In the simplest case

$ inline $ k $ inline $

denotes the size (capacity) of the backpack, and each of the numbers

$ inline $ a_i $ inline $

indicates the size (weight) of an item that can be packed into a backpack. The task is to find such a set of items so that the

backpack is completely filled.

Ie, imagine that you have a set of weights 1, 6, 8, 15 and 24, you need to pack a backpack with a weight of 30.

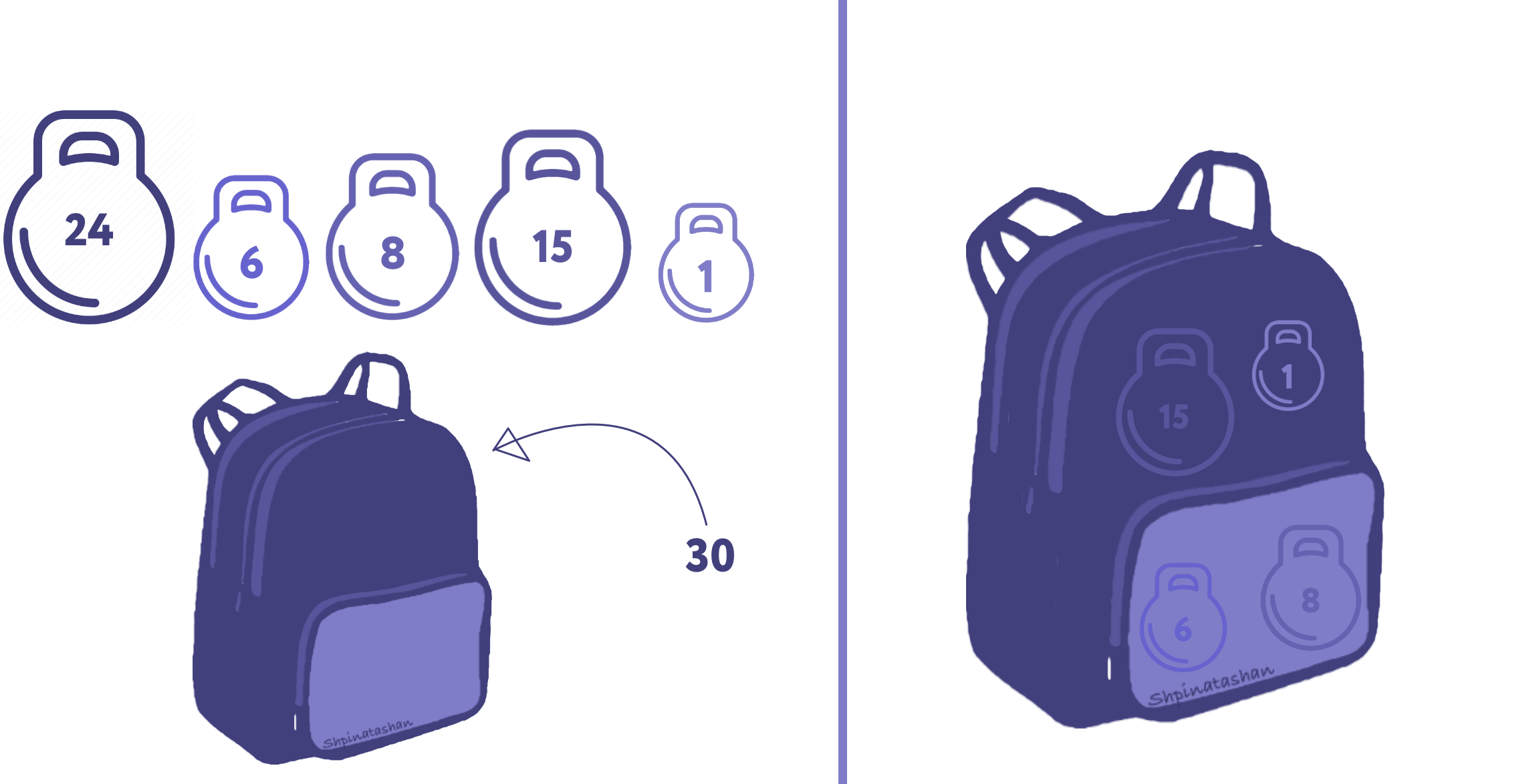
In principle, a solution can always be found by exhaustive search of subsets

$ inline $ A $ inline $

and checking which of their sums is

$ inline $ k $ inline $

... In our case, this means brute force

$ inline $ 2 ^ 5 = 32 $ inline $

subsets (including the empty set). This is quite feasible.

But what if there are several hundred numbers $$ inline $ a_i $ inline $$ ?

In our example, n = 5 in order not to complicate the presentation. In real conditions, an example will have, say, 300

$ inline $ a_i-x $ inline $

... The point here is that no algorithms are known that have a significantly lower complexity compared to exhaustive search. Search among

$ inline $ 2 ^ {300} $ inline $

subsets cannot be processed. Indeed, the knapsack problem is known as NP-complete ... NP-complete problems are considered difficult to compute.

Does the function meet the specified requirements?

We define the function

$ inline $ f (x) $ inline $

in the following way. Any number

$ inline $ 0 ≤ x ≤ 2n - 1 $ inline $

can be given by a binary representation from

$ inline $ n $ inline $

bits, where leading zeros are added if necessary. Now let's define

$ inline $ f (x) $ inline $

as a number obtained from

$ inline $ A $ inline $

summing up all such

$ inline $ a_i $ inline $

that the corresponding bit in binary notation

$ inline $ x $ inline $

equals 1.

That is,

$$$ display $$ f (1) = f (0.. 001) = a_n $$ display $$$

$$$ display $$ f (2) = f (0.. 010) = a_ {n − 1} $$ display $$$

$$$ display $$ f (3) = f (0.. 011) = a_ {n − 1} + a_n $$ display $$$

$$$ display $$ ... $$ display $$$

Function

$ inline $ f (x) $ inline $

was determined

$ inline $ n- $ inline $

set

$ inline $ A $ inline $

... Obviously, if we are able to compute

$ inline $ x $ inline $

$ inline $ f (x) $ inline $

, then in practically the same time the knapsack problem will be solved:

$ inline $ x $ inline $

its binary representation is immediately computed, which in turn gives the components of the set

$ inline $ A $ inline $

included in the sum for

$ inline $ f (x) $ inline $

... On the other hand, the calculation

$ inline $ f (x) $ inline $

$ inline $ x $ inline $

is lightweight. Since the knapsack problem is NP-complete,

$ inline $ f (x) $ inline $

is a good candidate for a one-way function. Of course, one must demand that $$ inline $ n $ inline $$ was big enough, say no less $$ inline $ 200 $ inline $$ ...

Encryption

Plain text

(. plain text) — , , . ( ).

You can encrypt in two ways:

The message cipher is obtained by raising the elements of this knapsack vector to the power of the corresponding bits of the encrypted message and then multiplying all the results, that is, if $$ inline $ A = (2,3,5) $ inline $$ and the message $$ inline $ (100) $ inline $$ , then the cipher will be the number $$ inline $ 2 ^ 1 * 3 ^ 0 * 5 ^ 0 = 2 $ inline $$ ... This is a multiplicative way.
The message cipher is obtained by multiplying the elements of this knapsack vector by the corresponding bits of the encrypted message and then summing up all the results, that is, if $$ inline $ A = (2,3,5) $ inline $$ and the message $$ inline $ (100) $ inline $$ , then the cipher will be the number $$ inline $ 2 ^ * 1 + 3 ^ * 0 + 5 ^ * 0 = 2 $ inline $$ ... This method is called additive .

Example

To encrypt plaintext in binary representation, it is split into blocks of length

$ inline $ n $ inline $

(for example, you can represent weight 30 with binary 11110). It is believed that one indicates the presence of an item in the backpack, and zero indicates its absence.

Backpack encryption provides a good approach to generating public and private keys, where the private key is easy to use and the public key is hard to figure out.

So, we can create a system where: the "hard" problem will serve as the

public key ; with it, you can easily encrypt and it is impossible to decrypt the message.

a private key - the "easy" problem will serve as using it, you can easily decrypt the message. Without the private key, you have to solve the "difficult" backpack problem.

"Easy" problem

Super growing backpack vector

A = (a_{1}, . . ., a_{n})

$A=(a_{1},...,a_{n})$ ,

Σ_{i = 1}^{j - 1} a_{i} < a_{j}

$Σ_{i=1}^{j-1} a_{i} < a_{j}$

j = 2, . . ., n

$j=2,...,n$ , . .

For super-growing vectors Α, the knapsack problem is easily solvable. Those. the backpack is easy to assemble.

Let's take an example:

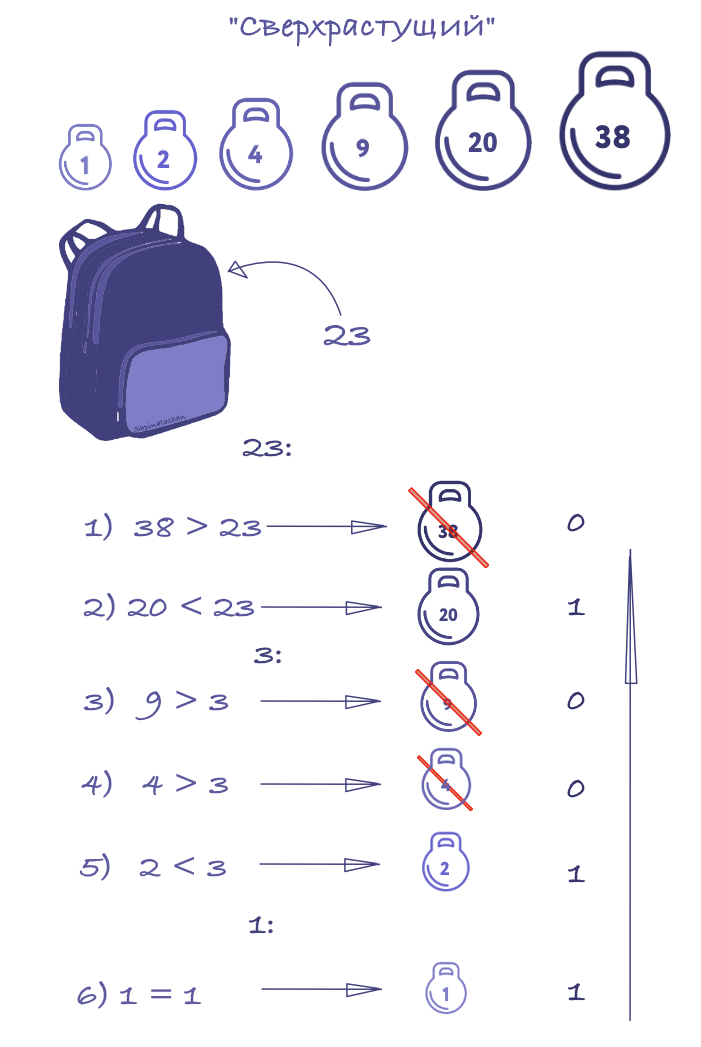
Algorithm

.

, , . , .
.
(1)-(2) .

, .

"Difficult" problem

It is much more difficult to decipher the problem of a non-oversized backpack.

One algorithm, which uses an oversized private key backpack and a non-oversized public key backpack, was created by Merkle and Hellman.

They did this by taking the oversized backpack task and transforming it into a non-oversizing task.

(Merkle and Hellman, using modular arithmetic, devised a way to transform a "light" backpack into a "hard" one)

Create a public key

Several important concepts

$(x, mod m)$ $x$ $m$ ,

$x$ — , $m > 1$ , [x/m] — ,
$x = (x, m o d m) + [x / m] * m$
$x = (x, mod m) + [x/m]*m$

$A$ , $m > max A$ $t < m$ , $(t, m) = 1$ .

$B = (b_1, . . . , b_n)$ , $b_i = (ta_i, modm)$ , $i = 1, . . . , n$ , , B A m t , , $(m, t)$ .

$(t, m) = 1$

$t^{−1} = u$ , ,

$t u \equiv 1 (m o d m)$
$tu ≡ 1 (mod m)$

$1 ≤ u < m$ . , $A$ $B$

$m, u$ .

$m > max A$

$m > Σ_{i=1}^{n} a_{i}$ , , $B$ $A$ $m, t$ .

— , , , .

The creator of the cryptosystem chooses such a system

$ inline $ A, t, m, B $ inline $

that vector

$ inline $ A $ inline $

is super-growing, and

$ inline $ B $ inline $

comes from

$ inline $ A $ inline $

strong modular multiplication with respect to

$ inline $ m, t $ inline $

... Vector

$ inline $ B $ inline $

expanded as encryption key and binary blocks of length

$ inline $ n $ inline $

sent to the designer as numbers

$ inline $ β $ inline $

obtained using the vector

$ inline $ B $ inline $

...

The message interceptor must solve the knapsack problem to enter

$ inline $ (B, β) $ inline $

... The creator of the cryptosystem calculates

$ inline $ α = (uβ, modm) $ inline $

and solves the backpack entry problem

$ inline $ (A, α) $ inline $

... Why all this works is

shown in the following lemma.

Lemma . Let's pretend that

$ inline $ A = (a_1,..., a_n) $ inline $

super growing vector and vector

$ inline $ B $ inline $

derived from

$ inline $ A $ inline $

strong modular multiplication with respect to

$ inline $ m, t $ inline $

... Suppose further that

$ inline $ u ≡ t ^ {- 1} (mod m) $ inline $

$ inline $ β $ inline $

- an arbitrary natural number and

$ inline $ α = (uβ, modm) $ inline $

... Then the following statements are true.

(i) The knapsack problem

$ inline $ (A, α) $ inline $

solvable in linear time. If a solution exists, then it is unique.

(ii) The knapsack problem

$ inline $ (B, β) $ inline $

has at most one solution.

(iii) If there is a solution to enter

$ inline $ (B, β) $ inline $

then it matches the only entry solution

$ inline $ (A, α) $ inline $

...

proof (p. 104)

Example

Consider a super-growing sequence; for example, {1, 2, 4, 10, 20, 40}. The modulus must be greater than the sum of all numbers in the sequence, for example 110. The multiplier must not have common divisors with the modulus. So let's pick 31.

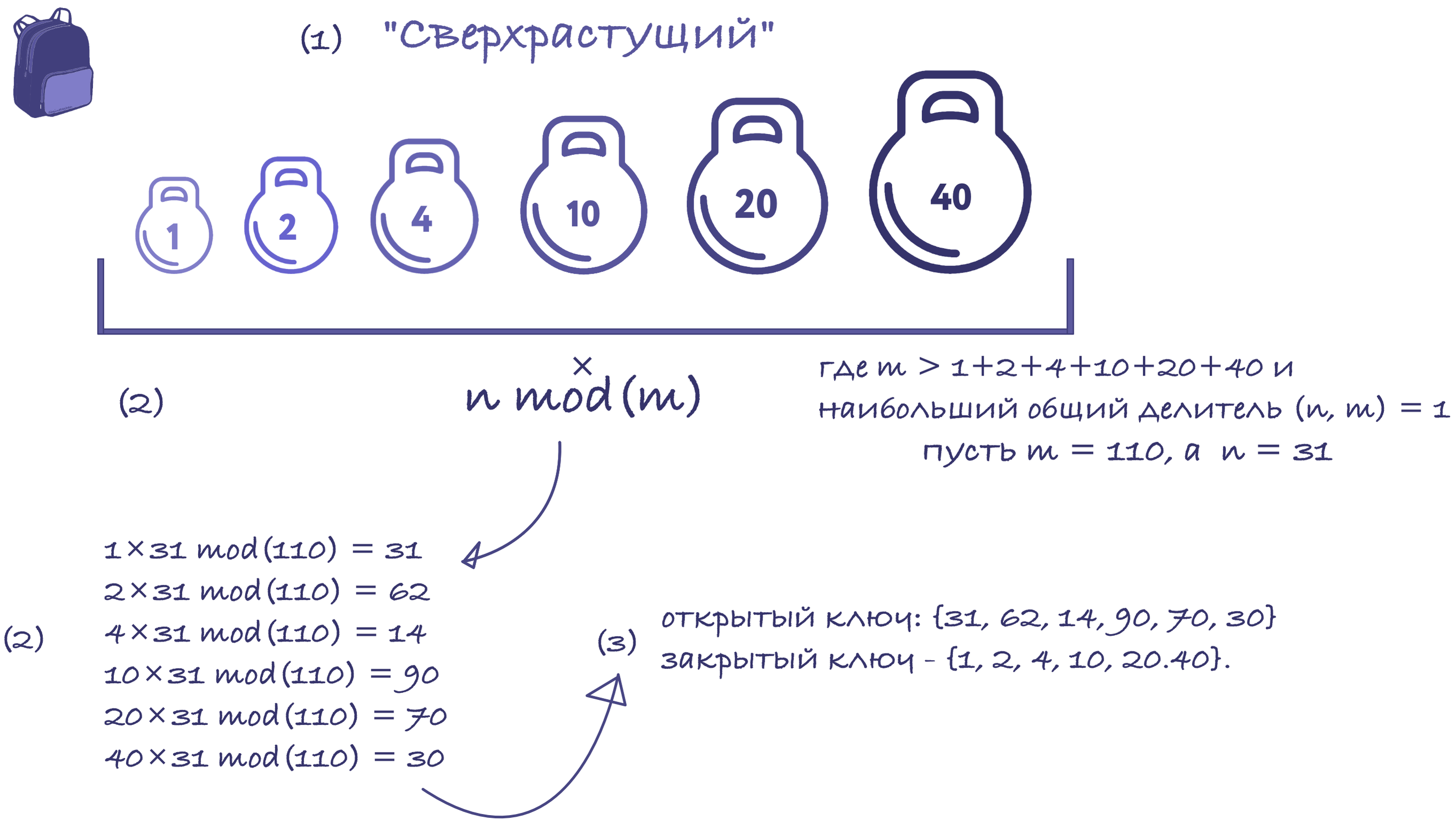
So, we calculated the public key: {31, 62, 14, 90, 70, 30} and the private key - {1, 2, 4, 10, 20.40}.

Now let's try to send a binary sequence: 100100111100101110

Some of the benefits of public keys

When using a public key cryptosystem, both parties do not meet, they may not even know each other and use any kind of communication.

Key length. In symmetric cryptography, if the key is longer than the original message, no real gain is achieved. As for public key cryptosystems, the length of the encryption key does not matter, since it is public and public. Therefore, the length of the decryption key is not so important (the recipient only stores it in a secret place)

History

For a long time, backpack cryptosystems were considered as the most attractive and promising cryptosystems due to their NP-completeness and high encryption and decryption speed. Many schemes use the knapsack problem (in various variations), here are just a few of them: the compact knapsack problem, the multiplicative knapsack problem, the modular knapsack problem, the matrixcover problem, the group factorization problem ...

Unfortunately, most of them are vulnerable to attacks. It turned out that it is not trivial to design a secure cryptosystem based on the knapsack problem, although the problem is known as NP-complete. Most knapsack cryptosystems have been hacked. Despite this, in contrast to integer factorization and discrete logarithm, the general knapsack (solution) problem is a proven NP-complete problem.

Some people think that one day a polynomial-time algorithm could be invented to solve integer factorization and discrete logarithm problems, while the knapsack problem is still NP-complete.

There are several "BUTs" here.

First, NP-completeness is based on worst-case analysis; second, NP-completeness is a characteristic of a general problem, not a specific case. This means that if we consider the average complexity, the knapsack problem can be easy.

The material was prepared on the basis of this literature:

(1) A. Salomaa. Public-Key Cryptography. - Springer-Verlag, 1990. - p. 75-82, pp. 101-111

(2)Min Kin Lai. Knapsack Cryptosystems : Past and Future - University of California, 2001

(3) Baocang Wang, Qianhong Wu, Yupu Hu. A knapsack-based probabilistic encryption scheme. 2007

(4) - (5)

Knapsack problem in cryptography