What did you say?

“Someone else has to say something that is clear to everyone” Such

an epigraph, Google / Yandex did not find the author



This is the second part of the article “What is clear to everyone”.

For a better understanding of the Z algorithm outlined in it, I will add here a good example given earlier in the discussion / comments.



Imagine that the task is to construct a curve of a certain function T (X) on a given interval of (permissible) values. It is desirable to do this in as much detail as possible, but you do not know in advance when they will "grab your hand". You want to generate X values ​​so that at any time when the plotting of the curve is interrupted (generating X parameters on an interval and calculating T (X)), the resulting graph reflects this function as accurately as possible. There will be more time - the graph will be more accurate, but - always the maximum of what is possible at the moment for an arbitrary function.



Of course, for a known function, the interval partitioning algorithm can take into account its behavior, but here we are talking about a general approach that gives the desired result with minimal "losses". For a two-dimensional case, you can give an example of displaying a certain relief / surface and want to be sure that as much as possible, you have displayed the maximum of its features.



The task and objects of modeling (from the first part) in the general case can be very different: there is a theoretical / physical model or an approximation or not (black box) - there will be nuances in building models everywhere. But the need to generate parameters (including the Z algorithm) is a common and integral part for everyone. There are objects (for example, such ) when the time for obtaining T is too long (days and weeks), then the algorithm for selecting a new step stops by other criteria, not because of the completion of the main calculation cycle in a parallel process. It makes no sense to further reduce the step to improve the search for the next forecast T if the expected improvement is obviously worse than the model error and / or measurement errors T.



I will give one more illustration of the division of the admissible interval for the two-dimensional case of the Z algorithm (K = 3 in the field 64 * 64):







The points highlighted in the figure (9 pcs.) Are the starting points of the edges and the middle of the interval, they, if necessary, are considered outside the Z algorithm. You can see that along the horizontal and vertical directions / "paths" that connect these points, generated by the algorithm Z values ​​are missing. Additional points here are easy to calculate separately, but with an increase in the number of points along these directions / "tracks", the representation of the function will improve (the "tracks" become narrower) and the need to supplement the algorithm itself (7 lines are needed, of which 4 operators are in the main loop in n, see below) or I do not see creating a separate calculation. Moreover, in this case, the average efficiency of the algorithm deteriorates, and there will be no significant improvement in the representation of the model (already for n> 8, the step in the parameter is less than 1/1000, see the table below).



The second feature of the Z algorithm is (for the two-dimensional case) the asymmetry in the order of adding points - on the Y axis / parameter they are on average more frequent, the picture is aligned at the end of each cycle by n.



Algorithm Z, one-dimensional case, in VBA language:

Xmax = 
Xmin = 
Dx = (Xmax - Xmin) / 2
L = 2
Sx = 0
For n = 1 To K
      Dx = Dx / 2
      D = Dx
      For j = 1 To L Step 2
            X = Xmin + D
				  Cells(5, X) = "O" '   - /   T(X)
            X = Xmax - D
				  Cells(5, X) = "O"
            D = D + Sx
       Next j
       Sx = Dx
       L = L + L
Next n

Algorithm Z, 2D case, VBA language:

Xmax = 		'	65 -    , GIF
Xmin = 		'	1
Ymax = 		'	65
Ymin = 		'	1
Dx = (Xmax - Xmin) / 2
Dy = (Ymax - Ymin) / 2
L = 2
Sx = 0
Sy = 0
For n = 1 To K		'	K = 3	  GIF
      Dx = Dx / 2
      Dy = Dy / 2
      Tx = Dx
      For j = 1 To L Step 2
	X1 = Xmin + Tx
        X2 = Xmax - Tx
	Ty = Dy
        For i = 1 To L Step 2
	   Y = Ymin + Ty
	   Cells(Y, X1) = "O" '   - /   T(Y,X)
	   Cells(Y, X2) = "O"
	   Y = Ymax - Ty
	   Cells(Y, X1) = "O"
	   Cells(Y, X2) = "O"
	   Ty = Ty + Sy
         Next i
       Tx = Tx + Sx
       Next j
       Sx = Dx
       Sy = Dy
       L = L + L
Next n

Computational costs:







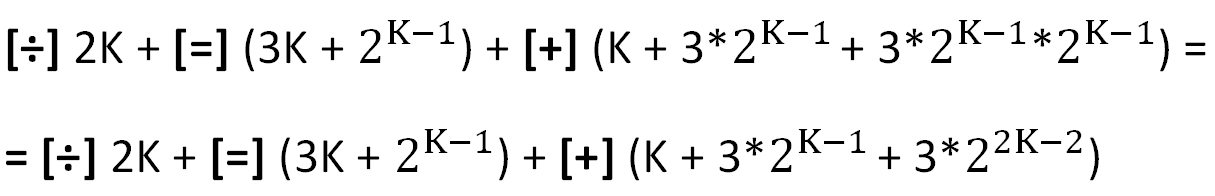
The main operations used in the calculations are indicated in square brackets (the costs of organizing cycles are not taken into account).



It should be noted here that the rather "heavy" operation of division [÷] in this case is not expensive, because integer division by 2 is a shift by one digit. The relative costs of the division and assignment operation ([=], second term) rapidly tend to zero with increasing K.



Total points:







Average costs:







For the first values ​​of K, we will carry out calculations using these formulas and fill in the table:





Here "fraction of the interval" is the relative step between points at the end of the cycle by n.

The last line ("average") shows the relative cost per point - the proportion of additions / subtractions. The limit tends to 0.5625 or 1 / 1.77777 of the addition operation.



Returning to the assertion from the first part of the article , it is shown here that “the algorithm proposed for discussion demonstrates extremely low computational costs and does not entail any drawbacks or difficulties," and in conditions of a sudden interruption of computations, it has additional advantages. It is wise to use it in all suitable applications.



I ask for help in distribution and implementation both in software and hardware.