This article is ad hoc. The last time I looked at the nuances and challenges of different data normalization methods. And only after the publication I realized that I had not mentioned some important details. To some, they will seem obvious, but, in my opinion, it is better to say about it explicitly.
Normalizing categorical data
In order not to clutter up the text with basic things, I will assume that you know what categorical and ordinal data are, and how they differ from the rest.
Obviously, any normalization can only be performed on numeric data. Accordingly, if only numbers are suitable for your algorithm / program for further work, then it is necessary to convert all other types to them.
Categorical data is simple. If the goal is not simply to encode (encrypt) the values with some numbers, then the only available option is to represent them as values “1” - “0” (YES - NO) for each possible category. This is the so-called one-hot encoding . When, instead of one categorical feature, as many new "boolean" features appear as there are possible categories.
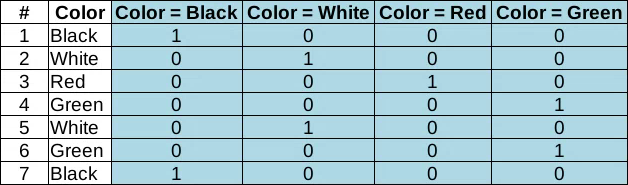
And that's all.
, .
, , .
, /”” , — . . .
, , , , “” “”. “ ”, , “” . , , — .
, - , « , 0 1». , . , .
. “” ( ) . , . .
1. . ( ). ( ) , , , . , , .

2. ( ). , “” .
, , . — , , , .
— ..
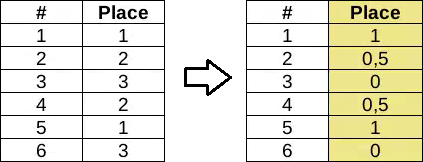
“”
, , . , .
. “” , . “” .
. , , , . — , , , ( ). .
“” , “”. .

. . , , 100 , 100 . 100 .
,
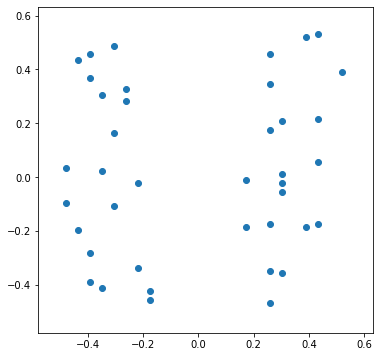
. “” , , . - , .
“” ( ) “” .

, , “”. .
“” “” .
. /, . “-” ( ), “-” ( ). , - , “-” , “-”.
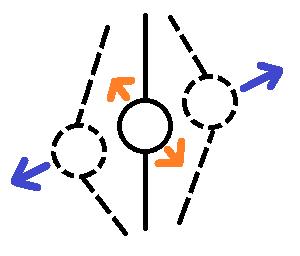
. . “” .
, , (- ), “-”, , “-”, . .. “”.
, “”, .
, — - , . - .
P.S. — , - AdjustedScaler, “” .