Smart data normalization

This article appeared for several reasons.

First, in the overwhelming majority of books, Internet resources and lessons on Data Science, the nuances, flaws of different types of data normalization and their reasons are either not considered at all, or are mentioned only in passing and without disclosing the essence.

Second, there is a "blind" use, for example, of standardization for sets with a large number of features - "so that it is the same for everyone." Especially for beginners (he himself was the same). At first glance, it's okay. But upon closer examination, it may turn out that some signs were unconsciously placed in a privileged position and began to influence the result much more strongly than they should.

And, thirdly, I always wanted to get a universal method that takes into account problem areas.

Repetition is the mother of learning

Normalization is the conversion of data to certain dimensionless units. Sometimes - within a given range, for example, [0..1] or [-1..1]. Sometimes - with some given property, such as, for example, a standard deviation of 1.

The key goal of normalization is to bring different data in a wide variety of units of measurement and ranges of values ​​to a single form that will allow you to compare them with each other or use to calculate the similarity of objects. In practice, this is necessary, for example, for clustering and in some machine learning algorithms.

Analytically, any normalization is reduced to the formula

$\$\$\; display\; \$\$\; Xnorm\; =\; (Xi\; -\; Xoffset)\; /\; Head\; \$\$\; display\; \$\$$

Where $\$\; inline\; \$\; Xi\; \$\; inline\; \$$ - present value,

$\$\; inline\; \$\; Xoffset\; \$\; inline\; \$$ - the value of the offset values,

$\$\; inline\; \$\; Head\; \$\; inline\; \$$ - the size of the interval to be converted to "one"

In fact, it all boils down to the fact that the original set of values ​​is first shifted and then scaled.

Examples:

Minimax (MinMax) . The goal is to convert the original set to the range [0..1]. For him:

$\$\; inline\; \$\; Xoffset\; \$\; inline\; \$$= $\$\; inline\; \$\; Xmin\; \$\; inline\; \$$, .

$$$X$ = $$$X$ — $$$X$, .. “” .

. — 0 1.

$$$X$= $$$X$, .

$$$X$ — .

, .

, , “” . .

, - . , . , , . , . , — . , , , , *

* — , , ( ), , .

, — .

1 —

— .. , , 0 “” .

? « » . .

№ 1 — , .

, “ ” , , — , . ( ). ( ) .

, , .

:

. “” .

, , , . .

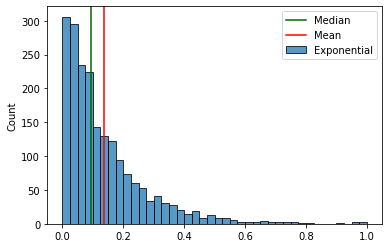
2 —

. .

. , , [-1..1], . [-1..1], — [-1..100], , . .

. . , “”.

( ):

( ) , .

, () “”, .

— ( ). , “” .

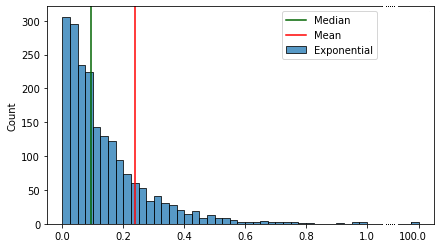
75- 25- — . .. , “” 50% . “” / .

— “”, “” .

№ 2 — “” .

— .

( ).

- “” . , , “”.

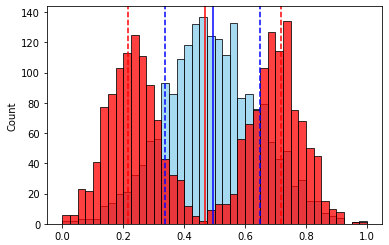
. .. . — 1.

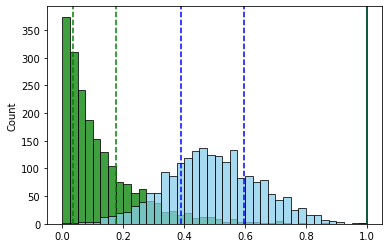
, , , № 3 — . ( ) .

, , . 2-

, , . .

, “-”. — .

— , . , . , , , , ? .

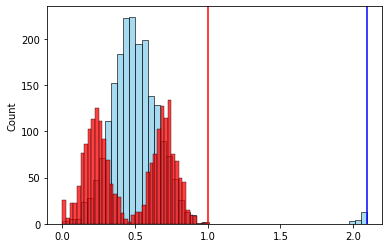
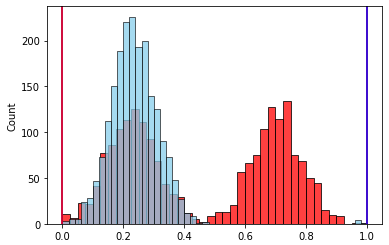
, . , “” , 1,5 (IQR) .*

* — ( .) 1,5 3 — .

.

— - , .

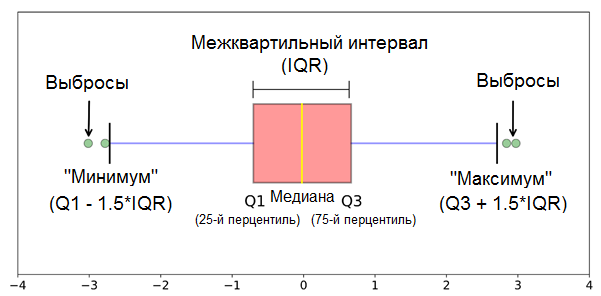
. (, , ) “” — 7%. (3 * IQR) — . . .. .

, . “ ” (1,5 * IQR) , . , - “” .

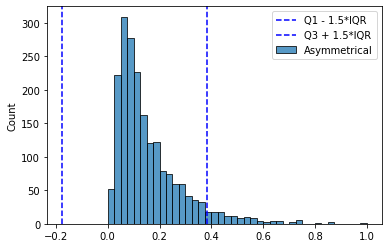
(Mia Hubert and Ellen Vandervieren) 2007 . “An Adjusted Boxplot for Skewed Distributions”.

“ ” , 1,5 * IQR.

“ ” medcouple (MC), :

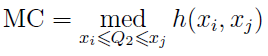
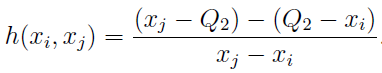
“ ” , , , 1,5 * IQR — 0,7%

:

$$$MC >= 0$:

$$$MC < 0$:

. .

, , :

1. , , .
2. .
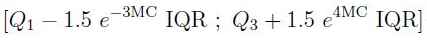
3. () — , , [0..1]

… — Mia Hubert Ellen Vandervieren

. .

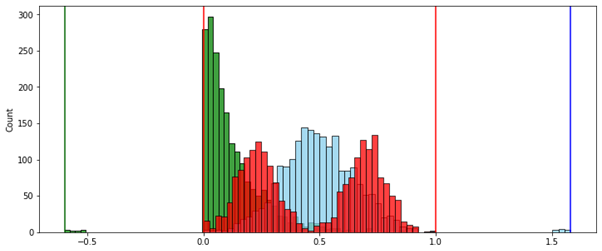
, ( ) (MinMax — ).

№ 1 — . . , “” .

:

( ):

:

, — , , .

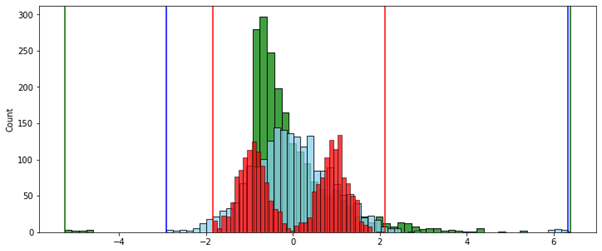
№ 2 — . [0..1]. , , .

MinMax ( ):

:

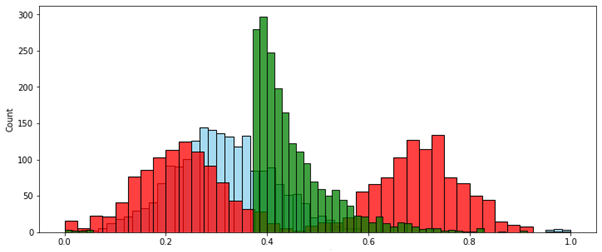
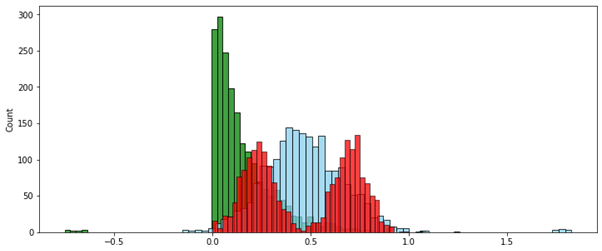
. -, , — .. 0 1.

, “” [0..1], , — , , , . .

* * *

Finally, for the opportunity to feel this method with your hands, you can try my demo class AdjustedScaler from here .

It is not optimized for working with a very large amount of data and only works with pandas DataFrame, but for trial, experimentation, or even a blank for something more serious, it is quite suitable. Try it.