
This is a translation of the second article in a series on differential privacy.
Last week, in the first article in this series - " Differential Privacy - Analyzing Data While Maintaining Confidentiality (Introduction to the Series) " - we looked at the basic concepts and uses of differential privacy. Today we will consider possible options for building systems, depending on the expected threat model.
Deploying a system that meets the principles of differential privacy is not a trivial task. As an example, in our next post, we'll look at a simple Python program that adds Laplace noise directly to a function that processes sensitive data. But in order for this to work, we need to collect all the required data on one server.
What if the server is hacked? In this case, differential privacy will not help us, because it only protects the data obtained as a result of the program's work!
When deploying systems based on the principles of differential privacy, it is important to consider the threat model: from which opponents we want to protect the system. If this model includes attackers capable of completely compromising a server with sensitive data, then we need to change the system so that it can withstand such attacks.
That is, the architectures of systems that respect differential privacy must consider both privacy and security . Privacy controls what can be retrieved from the data returned by the system. And security can be considered the opposite task: it is control over access to part of the data, but it does not give any guarantees regarding their content.
Central differential privacy model
The most commonly used threat model in differential privacy work is the central differential privacy model (or simply "central differential privacy").
The main component - the trusted data store (trusted data curator) . Each source sends him his confidential data, and it collects them in one place (for example, on a server). A repository is trusted if we assume that it processes our sensitive data on its own, does not transfer it to anyone, and cannot be compromised by anyone. In other words, we believe that a server with sensitive data cannot be hacked.
As part of the central model, we usually add noise to the responses to queries (we will look at the Laplace implementation in the next article). The advantage of this model is the ability to add the lowest possible noise value, thus maintaining the maximum accuracy allowed by the principles of differential privacy. Below is a diagram of the process. We have placed a privacy barrier between the trusted data store and the analyst so that only results that meet the specified differential privacy criteria can get outside. Thus, the analyst is not required to be trusted.
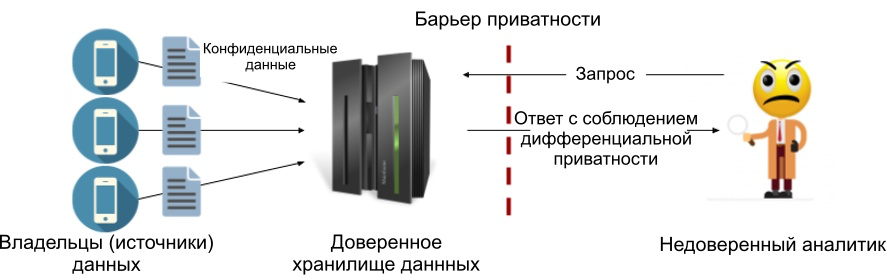
Figure 1: The central differential privacy model.
The disadvantage of the central model is that it requires a trusted store, and many of them are not. In fact, the lack of trust in the consumer of the data is usually the main reason for using differential privacy principles.
Local differential privacy model
The local differential privacy model allows you to get rid of the trusted data store: each data source (or data owner) adds noise to their data before transferring it to the store. This means that the storage will never contain sensitive information, which means that there is no need for its power of attorney. The figure below shows the device of the local model: in it, a privacy barrier is between each owner of the data and the storage (which may or may not be trusted).
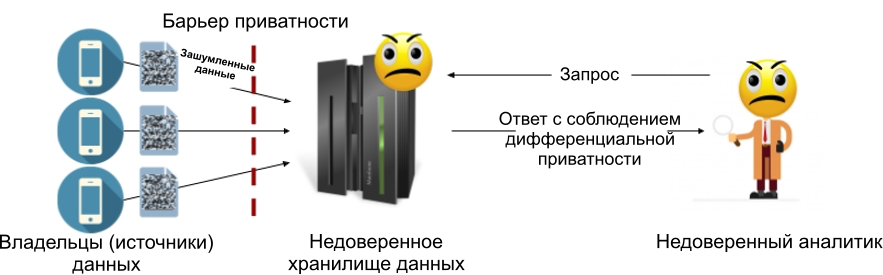
Figure 2: Local differential privacy model.
The local model of differential privacy avoids the main problem of the central model: if the data warehouse is compromised, then hackers will only have access to noisy data that already meets the requirements of differential privacy. This is the main reason why the local model was chosen for systems such as Google RAPPOR [1] and Apple's data collection system [2].
But on the other hand? The local model is less accurate than the central one. In the local model, each source independently adds noise to satisfy its own differential privacy conditions, so that the total noise from all participants is much greater than the noise in the central model.
Ultimately, this approach is only justified for queries with a very persistent trend (signal). Apple, for example, uses a local model to estimate the popularity of emoji, but the result is only useful for the most popular emoji (where the trend is most pronounced). Typically this model is not used for more complex queries such as those used by the US Census Bureau [10] or machine learning.
Hybrid models
The central and local models have both advantages and disadvantages, and the main effort now is to take the best from them.
For example, you can use the shuffling model implemented in the Prochlo system [4]. It contains an untrusted data store, many individual data owners, and several partially trusted shufflers.... Each source first adds a small amount of noise to its data and then sends it to the agitator, which adds more noise before sending it to the data warehouse. The bottom line is that agitators are unlikely to "collude" (or be hacked at the same time) with the data store or with each other, so a little noise added by the sources will be enough to guarantee privacy. Each mixer can handle multiple sources, just like the central model, so a small amount of noise will guarantee privacy for the resulting data set.
The agitator model is a compromise between local and central models: it adds less noise than local, but more than central.
You can also combine differential privacy with cryptography, as in secure multiparty computation (MPC) or fully homomorphic encryption (FHE). FHE allows computations with encrypted data without first decrypting them, and MPC allows a group of participants to safely execute queries over distributed sources without disclosing their data. Computation of Differential Private Functionsusing crypto-safe (or just secure) computing is a promising way to achieve central model accuracy with all the benefits of local. Moreover, in this case, the use of secure computing eliminates the need to have a trusted storage. Recent work [5] demonstrates encouraging results from the combination of MPC and differential privacy, absorbing most of the advantages of both approaches. True, in most cases, safe calculations are several orders of magnitude slower than locally performed ones, which is especially important for large data sets or complex queries. Secure computing is currently in active development phase, so its performance is rapidly increasing.
So?
In the next article, we'll take a look at our first open-source tool for putting differential privacy concepts into practice. Let's look at other tools, both available to newbies and applicable to very large databases, such as the US Census Bureau. We will try to calculate population data in compliance with the principles of differential privacy.
Subscribe to our blog and don't miss the translation of the next article. Very soon.
Sources
[1] Erlingsson, Úlfar, Vasyl Pihur, and Aleksandra Korolova. "Rappor: Randomized aggregatable privacy-preserving ordinal response." In Proceedings of the 2014 ACM SIGSAC conference on computer and communications security, pp. 1054-1067. 2014.
[2] Apple Inc. "Apple Differential Privacy Technical Overview." Accessed 7/31/2020. https://www.apple.com/privacy/docs/Differential_Privacy_Overview.pdf
[3] Garfinkel, Simson L., John M. Abowd, and Sarah Powazek. "Issues encountered deploying differential privacy." In Proceedings of the 2018 Workshop on Privacy in the Electronic Society, pp. 133-137. 2018.
[4] Bittau, Andrea, Úlfar Erlingsson, Petros Maniatis, Ilya Mironov, Ananth Raghunathan, David Lie, Mitch Rudominer, Ushasree Kode, Julien Tinnes, and Bernhard Seefeld. "Prochlo: Strong privacy for analytics in the crowd." In Proceedings of the 26th Symposium on Operating Systems Principles, pp. 441-459. 2017.
[5] Roy Chowdhury, Amrita, Chenghong Wang, Xi He, Ashwin Machanavajjhala, and Somesh Jha. "Cryptε: Crypto-Assisted Differential Privacy on Untrusted Servers." In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data, pp. 603-619. 2020.