Clever Geek Handbook

An autopsy will show: Solving a light crackme and writing a key generator

Good day, reader. I would like to tell you about the algorithm for solving one light crackme and share the generator code. This was one of the first crackme I solved.



In the vastness of the network, our pod was found. This is crackme . Naturally, it is necessary to study it. For the autopsy we need:



  • A bit of Assembler
  • Logic with debugger (IDA PRO)


Let's make a medicine from the venom of the Australian snake using Python. Let's not waste time.



image







This crackme is not very complicated. Consider the algorithm for generating a key on the correct key 8365-5794-2566-0817 . In IDA Pro, I added comments about the code.



Patient examination



At first glance, the behavior is normal. .Exe extension. Not packed. Let's start.











What is it? Requires a key. Need to heal :)



Autopsy of the patient



In case of an error, there was an inscription "Fail, Serial is invalid!". Let's take a place where it is used in the program.







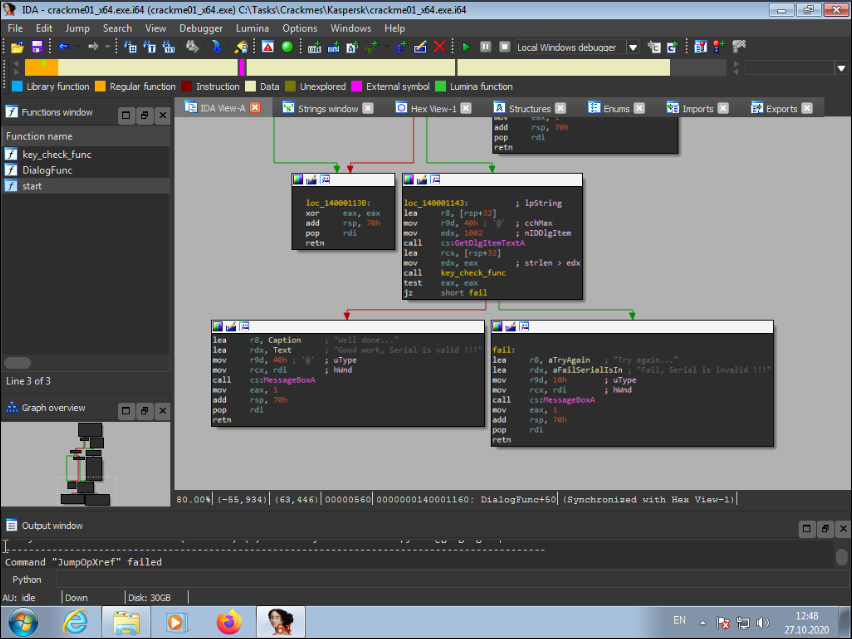
We see 1 function key_check_func before the conditional branch. Let's examine her.



An interesting tree turns out.







We set a breakpoint and start debugging.



The key must be 19 characters long.







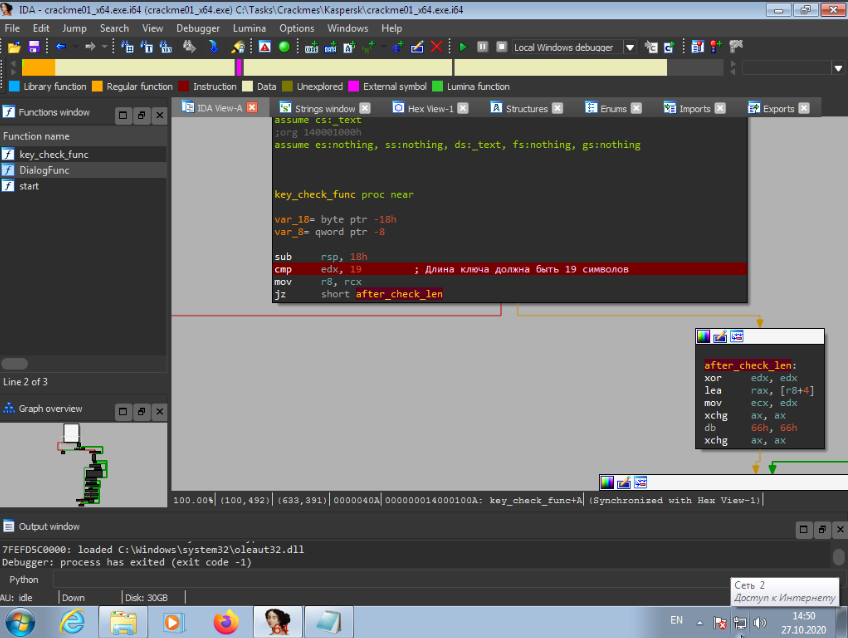
Then the program checks for the presence of a dash in the key every 5 characters, entering the loop 3 times.











After checking for the presence of a dash, the program examines whether the key block (1/4 key) consists of numbers. There is an assumption to understand which digit was passed to the compiler executing the command add eax, 0FFFFFFD0h







For example, add 8 (38h) with the given number. The resulting number is too large ( 10000008h) and at the end is 8, therefore, it is cut off. Remains 8. This is the figure we gave. This happens 4 times in a cycle.







Now what? Nowadays, the codes of each digit of the checked block are added to each other, but the last 4 digit is added 3 times in a row. The resulting amount is added up again. The code of the last digit of the block + the resulting amount is 150h. The result is added to r10d. This whole cycle is repeated 4 times for each key block.







In our case, consider the example of the first block of the key 8365: 38h (8) + 33h (3) + 36h (6) + 35h (5) + 35h (5) + 35h (5) = 140h + 35h - 150h = 25h. 25 is added to r10d and written to memory. Let's mark this place as A. The sum of other blocks of the key is also equal to 25h. Hence, we multiply 25h * 4 = 94.



Next, a bitwise shift to the right by 2 bytes occurs. We will mark this place for ourselves as B.







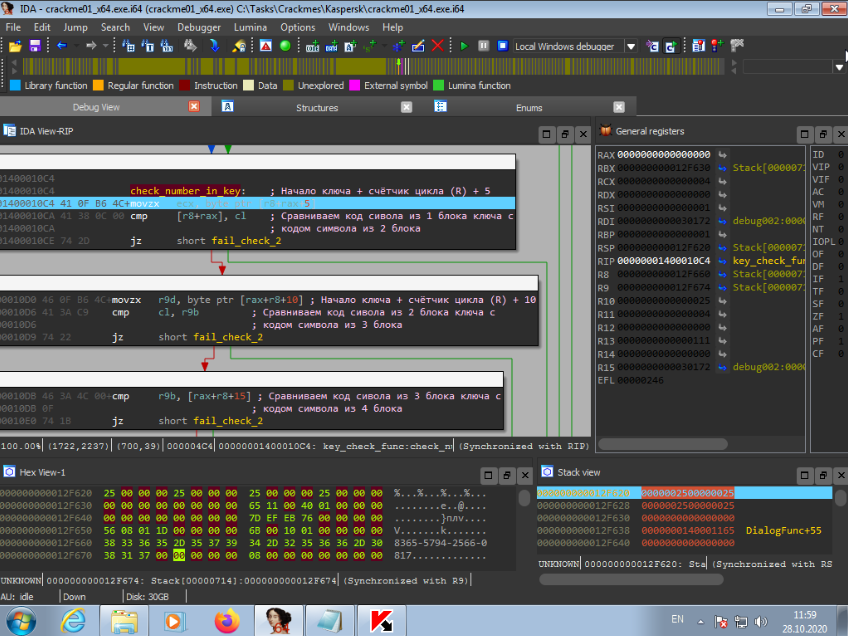
We have a value designated as A (25h) and B (25h). Subsequently, these numbers will be compared. They must be the same. This operation occurs for each key block.







The last thing the program does is check if the numbers in the blocks are similar. First, the digits of the 1st block are compared with the digits of the 2nd block. Then check 2 blocks with 3 blocks. Final check 3 blocks with 4 blocks. All this verification does not happen immediately, but gradually in a cycle.











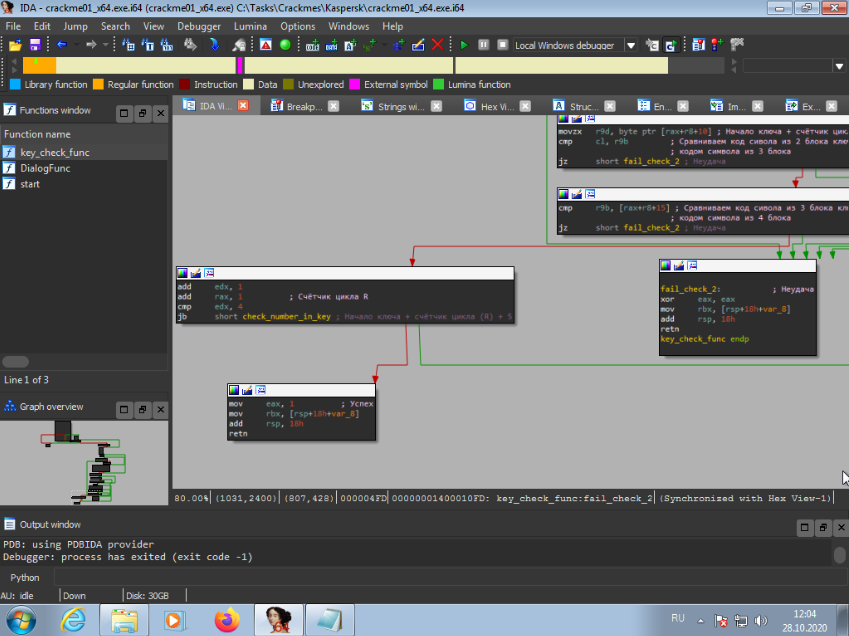
The analysis is over. The patient has been studied.



Time for a cure



We'll use something unusual to generate the key. Python + Library random.

The code itself is below. Comments in the code: 



import random

def gen_key_part():
    #  
    num1 = str(random.randint(0, 9))
    num2 = str(random.randint(0, 9))
    num3 = str(random.randint(0, 9))
    num4 = str(random.randint(0, 9))

    #    (1 )
    final = num1 + num2 + num3 + num4
    return final

def sum_ord(key_part):
    #      
    num1 = key_part[0]
    num2 = key_part[1]
    num3 = key_part[2]
    num4 = key_part[3]

    #    crackme
    sum = ord(num1) + ord(num2) + ord(num3) + ord(num4) + ord(num4) + ord(num4)
    sum_final = ord(num4) + sum - 336
    return sum_final

def shr(key):
    #    
    a = key[0:4]
    b = key[5:9]
    c = key[10:14]
    d = key[15:19]

    #      crackme
    x = sum_ord(a) + sum_ord(b) + sum_ord(c) + sum_ord(d)
    x = x >> 2
    return x

def check_key(key):
    i = 0 # 
    while i != 4:
        #  i    1  4.      
        first = 0 + i
        second = 5 + i
        third = 10 + i
        four = 15 + i

        #           ( ,  A  B)
        if sum_ord(key[0:4]) != shr(key) or sum_ord(key[5:9]) != shr(key) or sum_ord(key[10:14]) != shr(key) or sum_ord(key[15:19]) != shr(key):
            return False

        #     
        if int(key[first]) == int(key[second]):
            return False
        if int(key[second]) == int(key[third]):
            return False
        if int(key[third]) == int(key[four]):
            return False
        i += 1 # #  

def generate_key():
    #  
    key = gen_key_part() + '-' + gen_key_part() + '-' + gen_key_part() + '-' + gen_key_part()

    #     true  false
    while True: #
        if check_key(key) == False:
            #     
            key = gen_key_part() + '-' + gen_key_part() + '-' + gen_key_part() + '-' + gen_key_part()
            print('Checking this key -> ' + key)
        else:
            #  
            print('This is the correct key -> ' + key)
            break


#  ,  
if __name__ == "__main__":
    generate_key()


We launch.







Enter the key and see.







The patient is cured.



Thanks for attention. I look forward to your comments and criticism. Do not be ill.


More articles:


All Articles