
Anyone who has ever thought about how the graphics part of a 2D retro accelerator works, roughly represents how it draws these notorious Tiles, which, by the way, from the definition do not have to be rectangular. Tiling is about tiling. Yes, most often the developers of the iron api understand this and the methods are accordingly called drawRect and not drawTile. Any rectangle can indeed be a tile, but the reverse is not true! And then the question is brewing: Why 2D accelerators persistently accelerate only rect ... The simple answer to this question is because everything else is too complicated for a simple piece of hardware. But here I would argue. At least one simple but highly functional extension of this basic abstraction can be proposed, the following.
I haven't written to Habr for a long time. Because all the time I wanted to do it perfectly ... I have such a disease. Habr himself, meanwhile, has significantly lowered the bar, and I still do not write and do not write. Therefore, today's article was born without preparation from just a conversation with a friend. However, there are friends with whom you want to talk deeply and thoroughly.
Let it be, perhaps, my return to regularity. If such a plus or minus easy reading, with hastily thrown in a paint, but minimally sufficient for clarification, the narration is not overloaded with details, but still with a conceptual accent, and lamp-like, as once, will come to an expensive haber-reader.
In other words, today I am looking for a compromise between the quality of the content and the time I can devote to it. Hope for understanding.
So, let's begin…
Consider for a sample the general function of copying an arbitrary rectangular area. We see that this is just a double loop through the lines and through the elements of the lines:

Note that this block of code is usually trivially repeated in x4 combinations of directions of traversal of both loops to implement Reflections:

Another x2 combinations are given by the permutation of the order by dst [x] [y], reflecting along the axis y = x.
Along the way, these 8 options for reflections are all possible rotations in multiples of 90gr with all their mirror reflections from left to right.
And now let's look at how even with minimal additions this basic element could be greatly modified.
Perhaps it never occurred to anyone, but why can't a tile be, for example, a parallelepiped? Looking ahead, I will say that this extension carries minimal overhead, because to implement this, you need to add only a couple of increments per line:
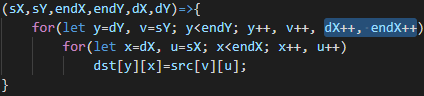
As a result of the combination with the x / y permutation, we get a parallelepiped with a pair of sides always oriented along one orthogonal, and the other two will be at an angle ... What does this cheaply received trifle give us? Well, firstly, the ability to use three fixed projections:
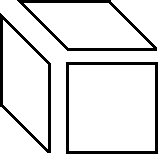
If the increment is made not a constant, but a fractional number, the shift angle can become free. Which can be perfectly used both for the effects of swaying tiles in the side scroller:
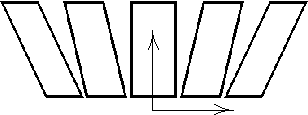
And for building walls in the space of isometric projections:

And remember that speaking fractional does not necessarily mean float support! What a modern spoiled programmer sometimes starts to forget about. float is fractional with Floating point, but here it is completely unnecessary. In fact, any processor with double registers, where the upper of the pair can be read as a separate value, has “support” for fractional fixed point (fixed point). Moreover, in this case, NOT a single extra instruction will be added. (Well, except that the slope will be set in 256th beats) So it's all free, take guys!
Another similar step that the attentive reader should inductively ask for is the repetition of this functional to the second boundary of the enumeration of the inner loop. After all, we can decouple the end increment separately. And then, in the general case, we will be able to draw any trapezoid based on one of the orthogonals (as a special case of triangles):

And what the hell did they give up to us? You’ll think, but you’ll immediately guess that in just two such drawing calls, you are simply texturing a plane from orthogonally oriented hexagons or diagonally oriented rhombuses from a tileset prepared for this. Tiling cases that are quite common in the game industry, by the way.
In the days of J2ME
J2ME , . , ,
It would be great to have hardware support for them on the accelerator: The

rest described is more of a bonus functionality, since you can better implement it purposefully. However, if we talk, among other things, only about filling the primitive with only color (or a flat pattern), for some simple additions to the existing game space ...
The same pair of draw calls can make up any triangle that is not limited to particulars (it is simply cut into two by an orthogonal line along the middle point, this is very similar to his classic drawing algorithm) And from this you can already build constructions in perspective. By the way, from the trapezoids themselves, for example, a vertically fixed 3D projection DOOM1 of the form is obtained elementarily cheaply:
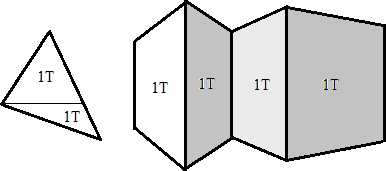
If you wish, you can try to paint with fill even something more or less large-voxel. Depending on the degrees of freedom of the projection, spending more or less draw calls. The first two perspective projections below are fixed but each has 4 symmetrical views - for a total of 8 display angles. The third is a common case and is fixed only vertically. Rotating around the vertical axis, it will alternate between the first and the second:

It is better to split the figures into trapeziums, if possible, into pieces that are more elongated along the orthogonal of the cut, because the additional call functionality, although not expensive, is associated with iterations of the outer only cycle, of which it is desirable that there would be fewer. In fact, this is true even for drawing the basic rectangle algorithm - drawing horizontal is more efficient than vertical drawing.
It is possible to perform perspective texturing on the bonus functionality in these calls, but it requires the implementation of fractional scaling and is associated with the introduction of additional divergence coefficients for src, and decimation coefficients, which, moreover, will need to be calculated in dynamics in 3D rather crookedly, which is not advisable for this simple architecture.
Well, ending the revenge before Habr for my own interest, I still can't help explaining briefly where all this magic of the increment coefficients comes from algebraically. The formula of the straight line y = kx + b, which is taught in schools, sends us hello here twice at once. All the coefficients came in handy in their places:

Why haven't I come across 2D hardware accelerators with such an implementation of tiles, I can only guess:
- Tile's concept was such a rigidly fixed pattern in practice that no one thought they could do a little more ... get a lot more.
- Either no one wanted to spend even a couple of cycles on such functions, because they did not analyze the widely spread consequences stated, or the developers of that time with simple games did not create demand for them. Nevertheless, there was mode7 (a cheat algorithm for implementing perspective texturing, through the output of pieces of rectangular sprites on hardware with support for fractional scaling)
- Or I'm not old enough, and I need to go on ...