
Looking for a goal
We go to the thematic site miniclip.com and look for a target. The choice fell on the Coloruid 2 color puzzle of the Puzzles section, in which we need to fill a round playing field with one color in a given number of moves.
An arbitrary area is filled with the color selected at the bottom of the screen, while adjacent areas of the same color merge into a single one.

Training
We will use Python. The bot was created solely for educational purposes. The article is intended for beginners in computer vision, which I myself am.
The game is located here
GitHub of the bot here
For the bot to work, we need the following modules:
- opencv-python
- Pillow
- selenium
The bot is written and tested for Python 3.8 on Ubuntu 20.04.1. We install the necessary modules into your virtual environment or via pip install. Additionally, for Selenium to work, we need a geckodriver for FireFox, you can download it here github.com/mozilla/geckodriver/releases
Browser control
We are dealing with an online game, so first we will organize interaction with the browser. For this purpose, we will use Selenium, which will provide us with an API for managing FireFox. Examining the code of the game page. The puzzle is a canvas, which in turn is located in an iframe.
We wait for the frame with id = iframe-game to load and switch the driver context to it. Then we wait for canvas. It is the only one in the frame and is available via XPath / html / body / canvas.
wait(self.__driver, 20).until(EC.frame_to_be_available_and_switch_to_it((By.ID, "iframe-game")))
self.__canvas = wait(self.__driver, 20).until(EC.visibility_of_element_located((By.XPATH, "/html/body/canvas")))Next, our canvas will be available through the self .__ canvas property. All the logic of working with the browser comes down to taking a screenshot of the canvas and clicking on it at a given coordinate.
The complete code of Browser.py:
from selenium import webdriver
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.support.ui import WebDriverWait as wait
from selenium.webdriver.common.by import By
class Browser:
def __init__(self, game_url):
self.__driver = webdriver.Firefox()
self.__driver.get(game_url)
wait(self.__driver, 20).until(EC.frame_to_be_available_and_switch_to_it((By.ID, "iframe-game")))
self.__canvas = wait(self.__driver, 20).until(EC.visibility_of_element_located((By.XPATH, "/html/body/canvas")))
def screenshot(self):
return self.__canvas.screenshot_as_png
def quit(self):
self.__driver.quit()
def click(self, click_point):
action = webdriver.common.action_chains.ActionChains(self.__driver)
action.move_to_element_with_offset(self.__canvas, click_point[0], click_point[1]).click().perform()Game states
Let's get down to the game itself. All bot logic will be implemented in the Robot class. Let's divide the gameplay into 7 states and assign them methods for processing them. Let's highlight the training level separately. It contains a large white cursor indicating where to click, which will prevent the game from being recognized correctly.
- Welcome screen
- Level selection screen
- Color selection at the tutorial level
- Choosing an area at the teaching level
- Color selection
- Region selection
- Result of the move
class Robot:
STATE_START = 0x01
STATE_SELECT_LEVEL = 0x02
STATE_TRAINING_SELECT_COLOR = 0x03
STATE_TRAINING_SELECT_AREA = 0x04
STATE_GAME_SELECT_COLOR = 0x05
STATE_GAME_SELECT_AREA = 0x06
STATE_GAME_RESULT = 0x07
def __init__(self):
self.states = {
self.STATE_START: self.state_start,
self.STATE_SELECT_LEVEL: self.state_select_level,
self.STATE_TRAINING_SELECT_COLOR: self.state_training_select_color,
self.STATE_TRAINING_SELECT_AREA: self.state_training_select_area,
self.STATE_GAME_RESULT: self.state_game_result,
self.STATE_GAME_SELECT_COLOR: self.state_game_select_color,
self.STATE_GAME_SELECT_AREA: self.state_game_select_area,
}For greater stability of the bot, we will check whether the change in the game state has occurred successfully. If self.state_next_success_condition does not return True during self.state_timeout, we continue to process the current state, otherwise we switch to self.state_next. We will also translate the screenshot received from Selenium into a format that OpenCV understands.
import time
import cv2
import numpy
from PIL import Image
from io import BytesIO
class Robot:
def __init__(self):
# …
self.screenshot = []
self.state_next_success_condition = None
self.state_start_time = 0
self.state_timeout = 0
self.state_current = 0
self.state_next = 0
def run(self, screenshot):
self.screenshot = cv2.cvtColor(numpy.array(Image.open(BytesIO(screenshot))), cv2.COLOR_BGR2RGB)
if self.state_current != self.state_next:
if self.state_next_success_condition():
self.set_state_current()
elif time.time() - self.state_start_time >= self.state_timeout
self.state_next = self.state_current
return False
else:
try:
return self.states[self.state_current]()
except KeyError:
self.__del__()
def set_state_current(self):
self.state_current = self.state_next
def set_state_next(self, state_next, state_next_success_condition, state_timeout):
self.state_next_success_condition = state_next_success_condition
self.state_start_time = time.time()
self.state_timeout = state_timeout
self.state_next = state_next
Let's implement the check in the state handling methods. We are waiting for the Play button on the start screen and click on it. If within 10 seconds we have not received the level selection screen, we return to the previous stage self.STATE_START, otherwise we proceed to processing self.STATE_SELECT_LEVEL.
# …
class Robot:
DEFAULT_STATE_TIMEOUT = 10
# …
def state_start(self):
# Play
# …
if button_play is False:
return False
self.set_state_next(self.STATE_SELECT_LEVEL, self.state_select_level_condition, self.DEFAULT_STATE_TIMEOUT)
return button_play
def state_select_level_condition(self):
#
# …
Bot vision
Image thresholding
Let's define the colors that are used in the game. These are 5 playable colors and a cursor color for the tutorial level. We will use COLOR_ALL if we need to find all objects, regardless of color. To begin with, we will consider this case.
COLOR_BLUE = 0x01
COLOR_ORANGE = 0x02
COLOR_RED = 0x03
COLOR_GREEN = 0x04
COLOR_YELLOW = 0x05
COLOR_WHITE = 0x06
COLOR_ALL = 0x07
To find an object, you first need to simplify the image. For example, let's take the symbol "0" and apply thresholding to it, that is, we will separate the object from the background. At this stage, we don't care what color the symbol is. First, let's convert the image to black and white, making it 1-channel. The cv2.cvtColor function with the second argument cv2.COLOR_BGR2GRAY , which is responsible for converting to grayscale , will help us with this . Next, we perform thresholding using cv2.threshold . All pixels of the image below a certain threshold are set to 0, everything above - to 255. The second argument of the cv2.threshold function is responsible for the threshold value . In our case, any number can be there, since we use cv2.THRESH_OTSU and the function will itself determine the optimal threshold by the Otsu method based on the image histogram.
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(image, 0, 255, cv2.THRESH_OTSU)

Color segmentation
Further more interesting. Let's complicate the task and find all the red symbols on the level selection screen.

By default, all OpenCV images are stored in BGR format. HSV (Hue, Saturation, Value - hue, saturation, value) is more suitable for color segmentation. Its advantage over RGB is that HSV separates color from its saturation and brightness. The hue is encoded by one Hue channel. Let's take a light green rectangle as an example and gradually decrease its brightness.
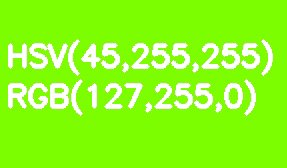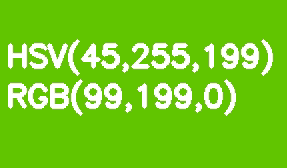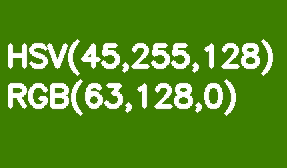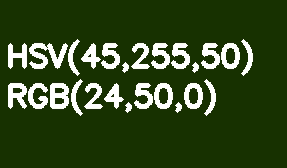
Unlike RGB, this transformation looks intuitive in HSV - we just decrease the value of the Value or Brightness channel. It should be noted here that in the reference model, the Hue shade scale varies in the range of 0-360 °. Our light green color corresponds to 90 °. In order to fit this value into an 8-bit channel, it should be divided by 2.
Color segmentation works with ranges, not a single color. You can determine the range empirically, but it's easier to write a small script.
import cv2
import numpy as numpy
image_path = "tests_data/SELECT_LEVEL.png"
hsv_max_upper = 0, 0, 0
hsv_min_lower = 255, 255, 255
def bite_range(value):
value = 255 if value > 255 else value
return 0 if value < 0 else value
def pick_color(event, x, y, flags, param):
if event == cv2.EVENT_LBUTTONDOWN:
global hsv_max_upper
global hsv_min_lower
global image_hsv
hsv_pixel = image_hsv[y, x]
hsv_max_upper = bite_range(max(hsv_max_upper[0], hsv_pixel[0]) + 1), \
bite_range(max(hsv_max_upper[1], hsv_pixel[1]) + 1), \
bite_range(max(hsv_max_upper[2], hsv_pixel[2]) + 1)
hsv_min_lower = bite_range(min(hsv_min_lower[0], hsv_pixel[0]) - 1), \
bite_range(min(hsv_min_lower[1], hsv_pixel[1]) - 1), \
bite_range(min(hsv_min_lower[2], hsv_pixel[2]) - 1)
print('HSV range: ', (hsv_min_lower, hsv_max_upper))
hsv_mask = cv2.inRange(image_hsv, numpy.array(hsv_min_lower), numpy.array(hsv_max_upper))
cv2.imshow("HSV Mask", hsv_mask)
image = cv2.imread(image_path)
cv2.namedWindow('Original')
cv2.setMouseCallback('Original', pick_color)
image_hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)
cv2.imshow("Original", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
Let's launch it with our screenshot.

Click on the red color and look at the resulting mask. If the output does not suit us, we choose the shades of red, increasing the range and area of the mask. The script is based on the cv2.inRange function , which acts as a color filter and returns a threshold image for a given color range.
Let's dwell on the following ranges:
COLOR_HSV_RANGE = {
COLOR_BLUE: ((112, 151, 216), (128, 167, 255)),
COLOR_ORANGE: ((8, 251, 93), (14, 255, 255)),
COLOR_RED: ((167, 252, 223), (171, 255, 255)),
COLOR_GREEN: ((71, 251, 98), (77, 255, 211)),
COLOR_YELLOW: ((27, 252, 51), (33, 255, 211)),
COLOR_WHITE: ((0, 0, 159), (7, 7, 255)),
}Finding contours
Let's go back to our level selection screen. Let's apply the red range color filter we just defined and pass the found threshold to cv2.findContours . The function will find us the outlines of the red elements. We specify cv2.RETR_EXTERNAL as the second argument - we only need outer contours, and cv2.CHAIN_APPROX_SIMPLE as the third - we are interested in straight contours, save memory and store only their vertices.
thresh = cv2.inRange(image, self.COLOR_HSV_RANGE[self.COLOR_RED][0], self.COLOR_HSV_RANGE[self.COLOR_RED][1])
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE
Noise removal
The resulting contours contain a lot of background noise. To remove it, we will use the property of our numbers. They are made up of rectangles that are parallel to the coordinate axes. We iterate over all the paths and fit each into the minimum rectangle using cv2.minAreaRect . The rectangle is defined by 4 points. If our rectangle is parallel to the axes, then one of the coordinates for each pair of points must match. This means we will have a maximum of 4 unique values if we represent the coordinates of the rectangle as a one-dimensional array. Additionally, let's filter out rectangles that are too long, where the aspect ratio is greater than 3 to 1. To do this, find their width and length using cv2.boundingRect .
squares = []
for cnt in contours:
rect = cv2.minAreaRect(cnt)
square = cv2.boxPoints(rect)
square = numpy.int0(square)
(_, _, w, h) = cv2.boundingRect(square)
a = max(w, h)
b = min(w, h)
if numpy.unique(square).shape[0] <= 4 and a <= b * 3:
squares.append(numpy.array([[square[0]], [square[1]], [square[2]], [square[3]]]))

Combining contours
Better. Now we need to combine the found rectangles into a common outline of symbols. We need an intermediate image. Let's create it with numpy.zeros_like . The function creates a copy of the image matrix while maintaining its shape and size, then fills it with zeros. In other words, we got a copy of our original image filled with a black background. We convert it to 1-channel and apply the found contours using cv2.drawContours , filling them with white. We get a binary threshold to which we can apply cv2.dilate . The function expands the white area by connecting separate rectangles, the distance between which is within 5 pixels. Once again I call cv2.findContours and get the contours of red numbers.
image_zero = numpy.zeros_like(image)
image_zero = cv2.cvtColor(image_zero, cv2.COLOR_BGR2RGB)
cv2.drawContours(image_zero, contours_of_squares, -1, (255, 255, 255), -1)
_, thresh = cv2.threshold(image_zero, 0, 255, cv2.THRESH_OTSU)
kernel = numpy.ones((5, 5), numpy.uint8)
thresh = cv2.dilate(thresh, kernel, iterations=1)
dilate_contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

The remaining noise is filtered by the contour area using cv2.contourArea . Remove everything that is less than 500 pixels².
digit_contours = [cnt for cnt in digit_contours if cv2.contourArea(cnt) > 500]
Now that's great. Let's implement all of the above in our Robot class.
# ...
class Robot:
# ...
def get_dilate_contours(self, image, color_inx, distance):
thresh = self.get_color_thresh(image, color_inx)
if thresh is False:
return []
kernel = numpy.ones((distance, distance), numpy.uint8)
thresh = cv2.dilate(thresh, kernel, iterations=1)
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
return contours
def get_color_thresh(self, image, color_inx):
if color_inx == self.COLOR_ALL:
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(image, 0, 255, cv2.THRESH_OTSU)
else:
image = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)
thresh = cv2.inRange(image, self.COLOR_HSV_RANGE[color_inx][0], self.COLOR_HSV_RANGE[color_inx][1])
return thresh
def filter_contours_of_rectangles(self, contours):
squares = []
for cnt in contours:
rect = cv2.minAreaRect(cnt)
square = cv2.boxPoints(rect)
square = numpy.int0(square)
(_, _, w, h) = cv2.boundingRect(square)
a = max(w, h)
b = min(w, h)
if numpy.unique(square).shape[0] <= 4 and a <= b * 3:
squares.append(numpy.array([[square[0]], [square[1]], [square[2]], [square[3]]]))
return squares
def get_contours_of_squares(self, image, color_inx, square_inx):
thresh = self.get_color_thresh(image, color_inx)
if thresh is False:
return False
contours, _ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
contours_of_squares = self.filter_contours_of_rectangles(contours)
if len(contours_of_squares) < 1:
return False
image_zero = numpy.zeros_like(image)
image_zero = cv2.cvtColor(image_zero, cv2.COLOR_BGR2RGB)
cv2.drawContours(image_zero, contours_of_squares, -1, (255, 255, 255), -1)
dilate_contours = self.get_dilate_contours(image_zero, self.COLOR_ALL, 5)
dilate_contours = [cnt for cnt in dilate_contours if cv2.contourArea(cnt) > 500]
if len(dilate_contours) < 1:
return False
else:
return dilate_contours
Recognition of numbers
Let's add the ability to recognize numbers. Why do we need this?
# …
class Robot:
# ...
SQUARE_BIG_SYMBOL = 0x01
SQUARE_SIZES = {
SQUARE_BIG_SYMBOL: 9,
}
IMAGE_DATA_PATH = "data/"
def __init__(self):
# ...
self.dilate_contours_bi_data = {}
for image_file in os.listdir(self.IMAGE_DATA_PATH):
image = cv2.imread(self.IMAGE_DATA_PATH + image_file)
contour_inx = os.path.splitext(image_file)[0]
color_inx = self.COLOR_RED
dilate_contours = self.get_dilate_contours_by_square_inx(image, color_inx, self.SQUARE_BIG_SYMBOL)
self.dilate_contours_bi_data[contour_inx] = dilate_contours[0]
def get_dilate_contours_by_square_inx(self, image, color_inx, square_inx):
distance = math.ceil(self.SQUARE_SIZES[square_inx] / 2)
return self.get_dilate_contours(image, color_inx, distance)OpenCV uses the cv2.matchShapes function to compare contours based on Hu moments . It hides the implementation details from us by taking two paths as input and returning the comparison result as a number. The smaller it is, the more similar the contours are.
cv2.matchShapes(dilate_contour, self.dilate_contours_bi_data['digit_' + str(digit)], cv2.CONTOURS_MATCH_I1, 0)Compare the current contour digit_contour with all standards and find the minimum value of cv2.matchShapes. If the minimum value is less than 0.15, the digit is considered recognized. The threshold of the minimum value was found empirically. Let's also combine closely spaced symbols into one number.
# …
class Robot:
# …
def scan_digits(self, image, color_inx, square_inx):
result = []
contours_of_squares = self.get_contours_of_squares(image, color_inx, square_inx)
before_digit_x, before_digit_y = (-100, -100)
if contours_of_squares is False:
return result
for contour_of_square in reversed(contours_of_squares):
crop_image = self.crop_image_by_contour(image, contour_of_square)
dilate_contours = self.get_dilate_contours_by_square_inx(crop_image, self.COLOR_ALL, square_inx)
if (len(dilate_contours) < 1):
continue
dilate_contour = dilate_contours[0]
match_shapes = {}
for digit in range(0, 10):
match_shapes[digit] = cv2.matchShapes(dilate_contour, self.dilate_contours_bi_data['digit_' + str(digit)], cv2.CONTOURS_MATCH_I1, 0)
min_match_shape = min(match_shapes.items(), key=lambda x: x[1])
if len(min_match_shape) > 0 and (min_match_shape[1] < self.MAX_MATCH_SHAPES_DIGITS):
digit = min_match_shape[0]
rect = cv2.minAreaRect(contour_of_square)
box = cv2.boxPoints(rect)
box = numpy.int0(box)
(digit_x, digit_y, digit_w, digit_h) = cv2.boundingRect(box)
if abs(digit_y - before_digit_y) < digit_y * 0.3 and abs(
digit_x - before_digit_x) < digit_w + digit_w * 0.5:
result[len(result) - 1][0] = int(str(result[len(result) - 1][0]) + str(digit))
else:
result.append([digit, self.get_contour_centroid(contour_of_square)])
before_digit_x, before_digit_y = digit_x + (digit_w / 2), digit_y
return resultAt the output, the self.scan_digits method will return an array containing the recognized digit and the coordinate of the click on it. The click point will be the centroid of its outline.
# …
class Robot:
# …
def get_contour_centroid(self, contour):
moments = cv2.moments(contour)
return int(moments["m10"] / moments["m00"]), int(moments["m01"] / moments["m00"])We rejoice at the received digit recognition tool, but not for long. In addition to scale, Hu moments are also invariant to rotation and specularity. Therefore, the bot will confuse the numbers 6 and 9/2 and 5. Let's add an additional vertex check for these symbols. 6 and 9 will be distinguished by the upper right point. If it is below the horizontal center, then it is 6 and 9 for the opposite. For pair 2 and 5, check if the upper right point is on the right border of the symbol.
if digit == 6 or digit == 9:
extreme_bottom_point = digit_contour[digit_contour[:, :, 1].argmax()].flatten()
x_points = digit_contour[:, :, 0].flatten()
extreme_right_points_args = numpy.argwhere(x_points == numpy.amax(x_points))
extreme_right_points = digit_contour[extreme_right_points_args]
extreme_top_right_point = extreme_right_points[extreme_right_points[:, :, :, 1].argmin()].flatten()
if extreme_top_right_point[1] > round(extreme_bottom_point[1] / 2):
digit = 6
else:
digit = 9
if digit == 2 or digit == 5:
extreme_right_point = digit_contour[digit_contour[:, :, 0].argmax()].flatten()
y_points = digit_contour[:, :, 1].flatten()
extreme_top_points_args = numpy.argwhere(y_points == numpy.amin(y_points))
extreme_top_points = digit_contour[extreme_top_points_args]
extreme_top_right_point = extreme_top_points[extreme_top_points[:, :, :, 0].argmax()].flatten()
if abs(extreme_right_point[0] - extreme_top_right_point[0]) > 0.05 * extreme_right_point[0]:
digit = 2
else:
digit = 5

Analyzing the playing field
Let's skip the training level, it is scripted by clicking on the white cursor and start playing.
Let's imagine the playing field as a network. Each area of color will be a node that is linked to adjacent neighbors. Let's create a class self.ColorArea that will describe the color area / node.
class ColorArea:
def __init__(self, color_inx, click_point, contour):
self.color_inx = color_inx #
self.click_point = click_point #
self.contour = contour #
self.neighbors = [] # Let's define a list of self.color_areas nodes and a list of how often the color appears on the playing field self.color_areas_color_count . Crop the playing field from the canvas screenshot.
image[pt1[1]:pt2[1], pt1[0]:pt2[0]]Where pt1, pt2 are the extreme points of the frame. We iterate over all the colors of the game and apply the self.get_dilate_contours method to each . Finding the contour of the node is similar to how we were looking for the general contour of symbols, with the difference that there are no noise on the playing field. The shape of the nodes can be concave or have a hole, so the centroid will fall out of the shape and is not suitable as a click coordinate. To do this, find the extreme top point and drop it 20 pixels. The method is not universal, but in our case it works.
self.color_areas = []
self.color_areas_color_count = [0] * self.SELECT_COLOR_COUNT
image = self.crop_image_by_rectangle(self.screenshot, numpy.array(self.GAME_MAIN_AREA))
for color_inx in range(1, self.SELECT_COLOR_COUNT + 1):
dilate_contours = self.get_dilate_contours(image, color_inx, 10)
for dilate_contour in dilate_contours:
click_point = tuple(
dilate_contour[dilate_contour[:, :, 1].argmin()].flatten() + [0, int(self.CLICK_AREA)])
self.color_areas_color_count[color_inx - 1] += 1
color_area = self.ColorArea(color_inx, click_point, dilate_contour)
self.color_areas.append(color_area)
Linking areas
We will consider areas as neighbors if the distance between their contours is within 15 pixels. We iterate over each node with each, skipping the comparison if their colors match.
blank_image = numpy.zeros_like(image)
blank_image = cv2.cvtColor(blank_image, cv2.COLOR_BGR2GRAY)
for color_area_inx_1 in range(0, len(self.color_areas)):
for color_area_inx_2 in range(color_area_inx_1 + 1, len(self.color_areas)):
color_area_1 = self.color_areas[color_area_inx_1]
color_area_2 = self.color_areas[color_area_inx_2]
if color_area_1.color_inx == color_area_2.color_inx:
continue
common_image = cv2.drawContours(blank_image.copy(), [color_area_1.contour, color_area_2.contour], -1, (255, 255, 255), cv2.FILLED)
kernel = numpy.ones((15, 15), numpy.uint8)
common_image = cv2.dilate(common_image, kernel, iterations=1)
common_contour, _ = cv2.findContours(common_image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
if len(common_contour) == 1:
self.color_areas[color_area_inx_1].neighbors.append(color_area_inx_2)
self.color_areas[color_area_inx_2].neighbors.append(color_area_inx_1)
We are looking for the optimal move
We have all the information about the playing field. Let's start choosing a move. For this we need the node and color index. The number of move options can be determined by the formula:
Move options = Number of nodes * Number of colors - 1
For the previous playing field, we have 7 * (5-1) = 28 options. There are not many of them, so we can iterate over all the moves and choose the optimal one. Let's define the options as a matrix
select_color_weights , in which the row will be the node index, the color index column and the move weight cell. We need to reduce the number of nodes to one, so we will give priority to areas that have a unique color on the board and that will disappear after we move to them. Let's give +10 to weight for all node rows with a unique color. How often the color is found on the playing field, we have previously collected inself.color_areas_color_count
if self.color_areas_color_count[color_area.color_inx - 1] == 1:
select_color_weight = [x + 10 for x in select_color_weight]
Next, let's look at the colors of adjacent areas. If the node has neighbors of color_inx, and their number is equal to the total number of this color on the playing field, assign +10 to the cell weight. This will also remove the color_inx color from the field.
for color_inx in range(0, len(select_color_weight)):
color_count = select_color_weight[color_inx]
if color_count != 0 and self.color_areas_color_count[color_inx] == color_count:
select_color_weight[color_inx] += 10Let's give +1 to the cell weight for each neighbor of the same color. That is, if we have 3 red neighbors, the red cell will receive +3 to its weight.
for select_color_weight_inx in color_area.neighbors:
neighbor_color_area = self.color_areas[select_color_weight_inx]
select_color_weight[neighbor_color_area.color_inx - 1] += 1After collecting all the weights, we find the move with the maximum weight. Let's define which node and what color it belongs to.
max_index = select_color_weights.argmax()
self.color_area_inx_next = max_index // self.SELECT_COLOR_COUNT
select_color_next = (max_index % self.SELECT_COLOR_COUNT) + 1
self.set_select_color_next(select_color_next)Complete code to determine the optimal move.
# …
class Robot:
# …
def scan_color_areas(self):
self.color_areas = []
self.color_areas_color_count = [0] * self.SELECT_COLOR_COUNT
image = self.crop_image_by_rectangle(self.screenshot, numpy.array(self.GAME_MAIN_AREA))
for color_inx in range(1, self.SELECT_COLOR_COUNT + 1):
dilate_contours = self.get_dilate_contours(image, color_inx, 10)
for dilate_contour in dilate_contours:
click_point = tuple(
dilate_contour[dilate_contour[:, :, 1].argmin()].flatten() + [0, int(self.CLICK_AREA)])
self.color_areas_color_count[color_inx - 1] += 1
color_area = self.ColorArea(color_inx, click_point, dilate_contour, [0] * self.SELECT_COLOR_COUNT)
self.color_areas.append(color_area)
blank_image = numpy.zeros_like(image)
blank_image = cv2.cvtColor(blank_image, cv2.COLOR_BGR2GRAY)
for color_area_inx_1 in range(0, len(self.color_areas)):
for color_area_inx_2 in range(color_area_inx_1 + 1, len(self.color_areas)):
color_area_1 = self.color_areas[color_area_inx_1]
color_area_2 = self.color_areas[color_area_inx_2]
if color_area_1.color_inx == color_area_2.color_inx:
continue
common_image = cv2.drawContours(blank_image.copy(), [color_area_1.contour, color_area_2.contour],
-1, (255, 255, 255), cv2.FILLED)
kernel = numpy.ones((15, 15), numpy.uint8)
common_image = cv2.dilate(common_image, kernel, iterations=1)
common_contour, _ = cv2.findContours(common_image, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
if len(common_contour) == 1:
self.color_areas[color_area_inx_1].neighbors.append(color_area_inx_2)
self.color_areas[color_area_inx_2].neighbors.append(color_area_inx_1)
def analysis_color_areas(self):
select_color_weights = []
for color_area_inx in range(0, len(self.color_areas)):
color_area = self.color_areas[color_area_inx]
select_color_weight = numpy.array([0] * self.SELECT_COLOR_COUNT)
for select_color_weight_inx in color_area.neighbors:
neighbor_color_area = self.color_areas[select_color_weight_inx]
select_color_weight[neighbor_color_area.color_inx - 1] += 1
for color_inx in range(0, len(select_color_weight)):
color_count = select_color_weight[color_inx]
if color_count != 0 and self.color_areas_color_count[color_inx] == color_count:
select_color_weight[color_inx] += 10
if self.color_areas_color_count[color_area.color_inx - 1] == 1:
select_color_weight = [x + 10 for x in select_color_weight]
color_area.set_select_color_weights(select_color_weight)
select_color_weights.append(select_color_weight)
select_color_weights = numpy.array(select_color_weights)
max_index = select_color_weights.argmax()
self.color_area_inx_next = max_index // self.SELECT_COLOR_COUNT
select_color_next = (max_index % self.SELECT_COLOR_COUNT) + 1
self.set_select_color_next(select_color_next)
Let's add the ability to move between levels and enjoy the result. The bot works stably and completes the game in one session.
Output
The created bot has no practical use. But the author of the article sincerely hopes that a detailed description of the basic principles of OpenCV will help beginners understand this library at the initial stage.