
Implement and compare 4 popular neural network training optimizers: impulse optimizer, rms propagation, mini-batch gradient descent, and adaptive torque estimation. The repository, a lot of Python code and its output, visualizations and formulas are all under the cut.
Introduction
A model is the result of a machine learning algorithm running on some data. The model represents what has been learned by the algorithm. This is the "thing" that persists after running the algorithm on the training data and represents rules, numbers, and any other data structures specific to the algorithm and necessary for prediction.
What is an optimizer?
Before moving on to this, we need to know what a loss function is. The loss function is a measure of how well your prediction model predicts the expected outcome (or value). The loss function is also called the cost function (more information here ).
During training, we try to minimize loss of function and update parameters to improve accuracy. The neural network parameters are usually the link weights. In this case, the parameters are studied at the training stage. So, the algorithm itself (and the input data) adjusts these parameters. More information can be found here .
Thus, the optimizer is a method for achieving better results, helping to speed up learning. In other words, it is an algorithm used to make minor adjustments to parameters such as weights and learning rates to keep the model running correctly and quickly. Here's a basic overview of the various optimizers used in deep learning and a simple model to understand the implementation of that model. I highly recommend cloning this repository and making changes by observing the behavior patterns.
Some commonly used terms:
- Back propagation
The goals of backpropagation are simple: adjust each weight in the network according to how much it contributes to the overall error. If you iteratively reduce the error of each weight, you end up with a series of weights that give good predictions. We find the slope of each parameter for the loss function and update the parameters by subtracting the slope (more info here ).

- Gradient descent
Gradient descent is an optimization algorithm used to minimize a function by iteratively moving towards the steepest descent, defined by a negative gradient value. In deep learning, we use gradient descent to update model parameters (more info here ).
- Hyperparameters
A model hyperparameter is a configuration external to the model, the value of which cannot be estimated from the data. For example, the number of hidden neurons, the learning rate, etc. We cannot estimate the learning rate from the data (more information here ).
- Learning rate
The learning rate (α) is a tuning parameter in the optimization algorithm that determines the step size at each iteration while moving towards the minimum of the loss function (more information here).
Popular optimizers

Below are some of the most popular SEOs:
- Stochastic Gradient Descent (SGD).
- Momentum Optimizer.
- Root mean square propagation (RMSProp).
- Adaptive torque estimation (Adam).
Let's consider each of them in detail.
1. Stochastic gradient descent (especially mini-batch)
We use one example at a time when training the model (in pure SGD) and updating the parameter. But we have to use another one for the loop. It will take a lot of time. Therefore, we use mini-batch SGD.
Mini batch gradient descent seeks to balance the robustness of stochastic gradient descent and the efficiency of batch gradient descent. This is the most common implementation of gradient descent used in deep learning. In mini batch SGD, when training the model, we take a group of examples (e.g. 32, 64 examples, etc.). This approach works better because it only takes a single loop for the minibatch, not every example. Mini-packages are randomly selected for each iteration, but why? When mini-packets are randomly selected, then when stuck in local minimums, some noisy steps can lead to the exit from these minimums. Why do we need this optimizer?
- The parameter update rate is higher than in simple batch gradient descent, which allows for more reliable convergence by avoiding local minima.
- Batch updates provide a computationally more efficient process than stochastic gradient descent.
- If you have little RAM, then mini-packages are the best option. Batching is efficient due to the absence of all training data in memory and algorithm implementations.
How do I generate random mini-packets?
def RandomMiniBatches(X, Y, MiniBatchSize):
m = X.shape[0]
miniBatches = []
permutation = list(np.random.permutation(m))
shuffled_X = X[permutation, :]
shuffled_Y = Y[permutation, :].reshape((m,1)) #sure for uptpur shape
num_minibatches = m // MiniBatchSize
for k in range(0, num_minibatches):
miniBatch_X = shuffled_X[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
miniBatch_Y = shuffled_Y[k * MiniBatchSize:(k + 1) * MiniBatchSize,:]
miniBatch = (miniBatch_X, miniBatch_Y)
miniBatches.append(miniBatch)
#handeling last batch
if m % MiniBatchSize != 0:
# end = m - MiniBatchSize * m // MiniBatchSize
miniBatch_X = shuffled_X[num_minibatches * MiniBatchSize:, :]
miniBatch_Y = shuffled_Y[num_minibatches * MiniBatchSize:, :]
miniBatch = (miniBatch_X, miniBatch_Y)
miniBatches.append(miniBatch)
return miniBatches
What will be the format of the model?
I am giving an overview of the model in case you are new to deep learning. It looks something like this:
def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
L = len(hidden_size)
params = initilization(X.shape[1], hidden_size)
for i in range(1,num_iter):
MiniBatches = RandomMiniBatches(X, Y, 64) # GET RAMDOMLY MINIBATCHES
p , q = MiniBatches[2]
for MiniBatch in MiniBatches: #LOOP FOR MINIBATCHES
(MiniBatch_X, MiniBatch_Y) = MiniBatch
cache, A = model_forward(MiniBatch_X, params, L,keep_prob) #FORWARD PROPOGATIONS
cost = cost_f(A, MiniBatch_Y) #COST FUNCTION
grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob) #BACKWARD PROPAGATION
params = update_params(params, grad, beta=0.9,learning_rate=learning_rate)
return params
In the following figure, you can see there are huge swings in SGD. Vertical movement is not necessary: we only want horizontal movement. If you decrease vertical movement and increase horizontal movement, the model will learn faster, don't you agree?

How to minimize unwanted vibrations? The following optimizers minimize them and help speed up learning.
2. Impulse optimizer
There is a lot of wobble in SGD or gradient descent. You need to move forward, not up and down. We need to increase the learning rate of the model in the right direction, and we will do that with the momentum optimizer.

As you can see in the picture above, the Green Line of the Pulse Optimizer is faster than others. The importance of learning quickly can be seen when you have large datasets and many iterations. How to implement this optimizer?

The normal value for β is around 0.9. You
can see that we created two parameters - vdW, and vdb - from the backpropagation parameters. Consider the value β = 0.9, then the equation takes the form:
vdw= 0.9 * vdw + 0.1 * dw
vdb = 0.9 * vdb + 0.1 * dbAs you can see, vdw is more dependent on the previous value of vdw rather than dw. When the render is a graph, you can see that the momentum optimizer takes past gradients into account to smooth the update. This is why it is possible to minimize fluctuations. When we used SGD, the path taken by the mini-batch gradient descent oscillated towards convergence. The Momentum Optimizer helps reduce these fluctuations.
def update_params_with_momentum(params, grads, v, beta, learning_rate):
# grads has the dw and db parameters from backprop
# params has the W and b parameters which we have to update
for l in range(len(params) // 2 ):
# HERE WE COMPUTING THE VELOCITIES
v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads['dW' + str(l + 1)]
v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads['db' + str(l + 1)]
#updating parameters W and b
params["W" + str(l + 1)] = params["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
params["b" + str(l + 1)] = params["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
return params
The repository is here
3. Root mean square spread
Root root mean square (RMSprop) is an exponentially decaying mean. The essential property of RMSprop is that you are not limited only to the sum of past gradients, but you are more limited to the gradients of the last time steps. RMSprop contributes to the exponentially decaying mean of past “square-law gradients”. In RMSProp we are trying to reduce the vertical movement by using the mean, because they add up to about 0 by taking the mean. RMSprop provides the average for the update.

A source

Take a look at the below code. This will give you a basic understanding of how to implement this optimizer. Everything is the same as with SGD, we have to change the update function.
def initilization_RMS(params):
s = {}
for i in range(len(params)//2 ):
s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
return s
def update_params_with_RMS(params, grads,s, beta, learning_rate):
# grads has the dw and db parameters from backprop
# params has the W and b parameters which we have to update
for l in range(len(params) // 2 ):
# HERE WE COMPUTING THE VELOCITIES
s["dW" + str(l)]= beta * s["dW" + str(l)] + (1 - beta) * np.square(grads['dW' + str(l)])
s["db" + str(l)] = beta * s["db" + str(l)] + (1 - beta) * np.square(grads['db' + str(l)])
#updating parameters W and b
params["W" + str(l)] = params["W" + str(l)] - learning_rate * grads['dW' + str(l)] / (np.sqrt( s["dW" + str(l)] )+ pow(10,-4))
params["b" + str(l)] = params["b" + str(l)] - learning_rate * grads['db' + str(l)] / (np.sqrt( s["db" + str(l)]) + pow(10,-4))
return params
4. Adam Optimizer
Adam is one of the most efficient optimization algorithms in neural network training. It combines the ideas of RMSProp and Pulse Optimizer. Instead of adapting the learning rate of the parameters based on the mean of the first moment (mean), as in RMSProp, Adam also uses the mean of the second moments of the gradients. Specifically, the algorithm calculates the exponential moving average of the gradient and the quadratic gradient, and the parameters
beta1and beta2controls the decay rate of these moving averages. How?
def initilization_Adam(params):
s = {}
v = {}
for i in range(len(params)//2 ):
v["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
v["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
s["dW" + str(i)] = np.zeros(params["W" + str(i)].shape)
s["db" + str(i)] = np.zeros(params["b" + str(i)].shape)
return v, s
def update_params_with_Adam(params, grads,v, s, beta1,beta2, learning_rate,t):
epsilon = pow(10,-8)
v_corrected = {}
s_corrected = {}
# grads has the dw and db parameters from backprop
# params has the W and b parameters which we have to update
for l in range(len(params) // 2 ):
# HERE WE COMPUTING THE VELOCITIES
v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1 - beta1) * grads['dW' + str(l)]
v["db" + str(l)] = beta1 * v["db" + str(l)] + (1 - beta1) * grads['db' + str(l)]
v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - np.power(beta1, t))
v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - np.power(beta1, t))
s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1 - beta2) * np.power(grads['dW' + str(l)], 2)
s["db" + str(l)] = beta2 * s["db" + str(l)] + (1 - beta2) * np.power(grads['db' + str(l)], 2)
s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - np.power(beta2, t))
s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - np.power(beta2, t))
params["W" + str(l)] = params["W" + str(l)] - learning_rate * v_corrected["dW" + str(l)] / np.sqrt(s_corrected["dW" + str(l)] + epsilon)
params["b" + str(l)] = params["b" + str(l)] - learning_rate * v_corrected["db" + str(l)] / np.sqrt(s_corrected["db" + str(l)] + epsilon)
return params
Hyperparameters
- β1 (beta1) value almost 0.9
- β2 (beta2) - almost 0.999
- ε - prevent division by zero (10 ^ -8) (doesn't affect learning too much)
Why this optimizer?
Its advantages:
- Simple implementation.
- Computational efficiency.
- Low memory requirements.
- Invariant to diagonal scaling of gradients.
- Well suited for large tasks in terms of data and parameters.
- Suitable for non-stationary purposes.
- Suitable for tasks with very noisy or sparse gradients.
- Hyperparameters are straightforward and usually require little tuning.
Let's build a model and see how hyperparameters speed up learning
Let's do a hands-on demonstration of how to accelerate learning. In this article we will not explain the other things (initialization, screenings,
forward_prop, back_prop, gradient descent, and so on. D.). The functions required for training are already built into NumPy. If you want to take a look at it, here's the link !
Let's start!
I am creating a generic model function that works for all the optimizers discussed here.
1. Initialization:
We initialize the parameters using an initialization function that takes inputs such as
features_size (in our case 12288) and a hidden array of sizes (we used [100,1]) and this output as initialization parameters. There is another initialization method. I encourage you to read this article.
def initilization(input_size,layer_size):
params = {}
np.random.seed(0)
params['W' + str(0)] = np.random.randn(layer_size[0], input_size) * np.sqrt(2 / input_size)
params['b' + str(0)] = np.zeros((layer_size[0], 1))
for l in range(1,len(layer_size)):
params['W' + str(l)] = np.random.randn(layer_size[l],layer_size[l-1]) * np.sqrt(2/layer_size[l])
params['b' + str(l)] = np.zeros((layer_size[l],1))
return params
2. Forward Propagation:
In this function, the input is X, as well as the parameters, the extent of the hidden layers and the dropout, which are used in the dropout technique.
I set the value to 1 so that no effect will be seen in the workout. If your model is overfitted, then you can set a different value. I only apply the dropout on the even layers .
We calculate the activation value for each layer using a function
forward_activation.
#activations-----------------------------------------------
def forward_activation(A_prev, w, b, activation):
z = np.dot(A_prev, w.T) + b.T
if activation == 'relu':
A = np.maximum(0, z)
elif activation == 'sigmoid':
A = 1/(1+np.exp(-z))
else:
A = np.tanh(z)
return A
#________model forward ____________________________________________________________________________________________________________
def model_forward(X,params, L,keep_prob):
cache = {}
A =X
for l in range(L-1):
w = params['W' + str(l)]
b = params['b' + str(l)]
A = forward_activation(A, w, b, 'relu')
if l%2 == 0:
cache['D' + str(l)] = np.random.randn(A.shape[0],A.shape[1]) < keep_prob
A = A * cache['D' + str(l)] / keep_prob
cache['A' + str(l)] = A
w = params['W' + str(L-1)]
b = params['b' + str(L-1)]
A = forward_activation(A, w, b, 'sigmoid')
cache['A' + str(L-1)] = A
return cache, A
3. Backpropagation:
Here we write the backpropagation function. It will return grad ( slope ). We use
gradwhen updating the parameters (if you don't know about it). I recommend reading this article.
def backward(X, Y, params, cach,L,keep_prob):
grad ={}
m = Y.shape[0]
cach['A' + str(-1)] = X
grad['dz' + str(L-1)] = cach['A' + str(L-1)] - Y
cach['D' + str(- 1)] = 0
for l in reversed(range(L)):
grad['dW' + str(l)] = (1 / m) * np.dot(grad['dz' + str(l)].T, cach['A' + str(l-1)])
grad['db' + str(l)] = 1 / m * np.sum(grad['dz' + str(l)].T, axis=1, keepdims=True)
if l%2 != 0:
grad['dz' + str(l-1)] = ((np.dot(grad['dz' + str(l)], params['W' + str(l)]) * cach['D' + str(l-1)] / keep_prob) *
np.int64(cach['A' + str(l-1)] > 0))
else :
grad['dz' + str(l - 1)] = (np.dot(grad['dz' + str(l)], params['W' + str(l)]) *
np.int64(cach['A' + str(l - 1)] > 0))
return grad
We've already seen the optimizer update feature, so we'll use it here. Let's make some minor changes to the model function from the SGD discussion.
def model(X,Y,learning_rate,num_iter,hidden_size,keep_prob,optimizer):
L = len(hidden_size)
params = initilization(X.shape[1], hidden_size)
costs = []
itr = []
if optimizer == 'momentum':
v = initilization_moment(params)
elif optimizer == 'rmsprop':
s = initilization_RMS(params)
elif optimizer == 'adam' :
v,s = initilization_Adam(params)
for i in range(1,num_iter):
MiniBatches = RandomMiniBatches(X, Y, 32) # GET RAMDOMLY MINIBATCHES
p , q = MiniBatches[2]
for MiniBatch in MiniBatches: #LOOP FOR MINIBATCHES
(MiniBatch_X, MiniBatch_Y) = MiniBatch
cache, A = model_forward(MiniBatch_X, params, L,keep_prob) #FORWARD PROPOGATIONS
cost = cost_f(A, MiniBatch_Y) #COST FUNCTION
grad = backward(MiniBatch_X, MiniBatch_Y, params, cache, L,keep_prob) #BACKWARD PROPAGATION
if optimizer == 'momentum':
params = update_params_with_momentum(params, grad, v, beta=0.9,learning_rate=learning_rate)
elif optimizer == 'rmsprop':
params = update_params_with_RMS(params, grad, s, beta=0.9,learning_rate=learning_rate)
elif optimizer == 'adam' :
params = update_params_with_Adam(params, grad,v, s, beta1=0.9,beta2=0.999, learning_rate=learning_rate,t=i) #UPDATE PARAMETERS
elif optimizer == "minibatch":
params = update_params(params, grad,learning_rate=learning_rate)
if i%5 == 0:
costs.append(cost)
itr.append(i)
if i % 100 == 0 :
print('cost of iteration______{}______{}'.format(i,cost))
return params,costs,itr
Training with mini packs
params, cost_sgd,itr = model(X_train, Y_train, learning_rate = 0.01,
num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='minibatch')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))Conclusion when approaching with mini-packages:
cost of iteration______100______0.35302967575683797
cost of iteration______200______0.472914548745098
cost of iteration______300______0.4884728238471557
cost of iteration______400______0.21551100063345618
train_accuracy------------ 0.8494208494208494
Pulse Optimizer Training
params,cost_momentum, itr = model(X_train, Y_train, learning_rate = 0.01,
num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='momentum')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))Pulse optimizer output:
cost of iteration______100______0.36278494129038086
cost of iteration______200______0.4681552335189021
cost of iteration______300______0.382226159384529
cost of iteration______400______0.18219310793752702 train_accuracy------------ 0.8725868725868726Training with RMSprop
params,cost_rms,itr = model(X_train, Y_train, learning_rate = 0.01,
num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='rmsprop')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))RMSprop output:
cost of iteration______100______0.2983858963793841
cost of iteration______200______0.004245700579927428
cost of iteration______300______0.2629426607580565
cost of iteration______400______0.31944824707807556 train_accuracy------------ 0.9613899613899614Training with Adam
params,cost_adam, itr = model(X_train, Y_train, learning_rate = 0.01,
num_iter=500, hidden_size=[100, 1],keep_prob=1,optimizer='adam')
Y_train_pre = predict(X_train, params, 2)
print('train_accuracy------------', accuracy_score(Y_train_pre, Y_train))Adam's conclusion:
cost of iteration______100______0.3266223660473619
cost of iteration______200______0.08214547683157716
cost of iteration______300______0.0025645257286439583
cost of iteration______400______0.058015188756586206 train_accuracy------------ 0.9845559845559846Have you seen the difference in accuracy between the two? We used the same initialization parameters, the same learning rate, and the same number of iterations; only the optimizer is different, but look at the result!
Mini-batch accuracy : 0.8494208494208494
momemtum accuracy : 0.8725868725868726
Rms accuracy : 0.9613899613899614
adam accuracy : 0.9845559845559846Graphic visualization of the model

You can check the repository if you have doubts about the code.
Summary
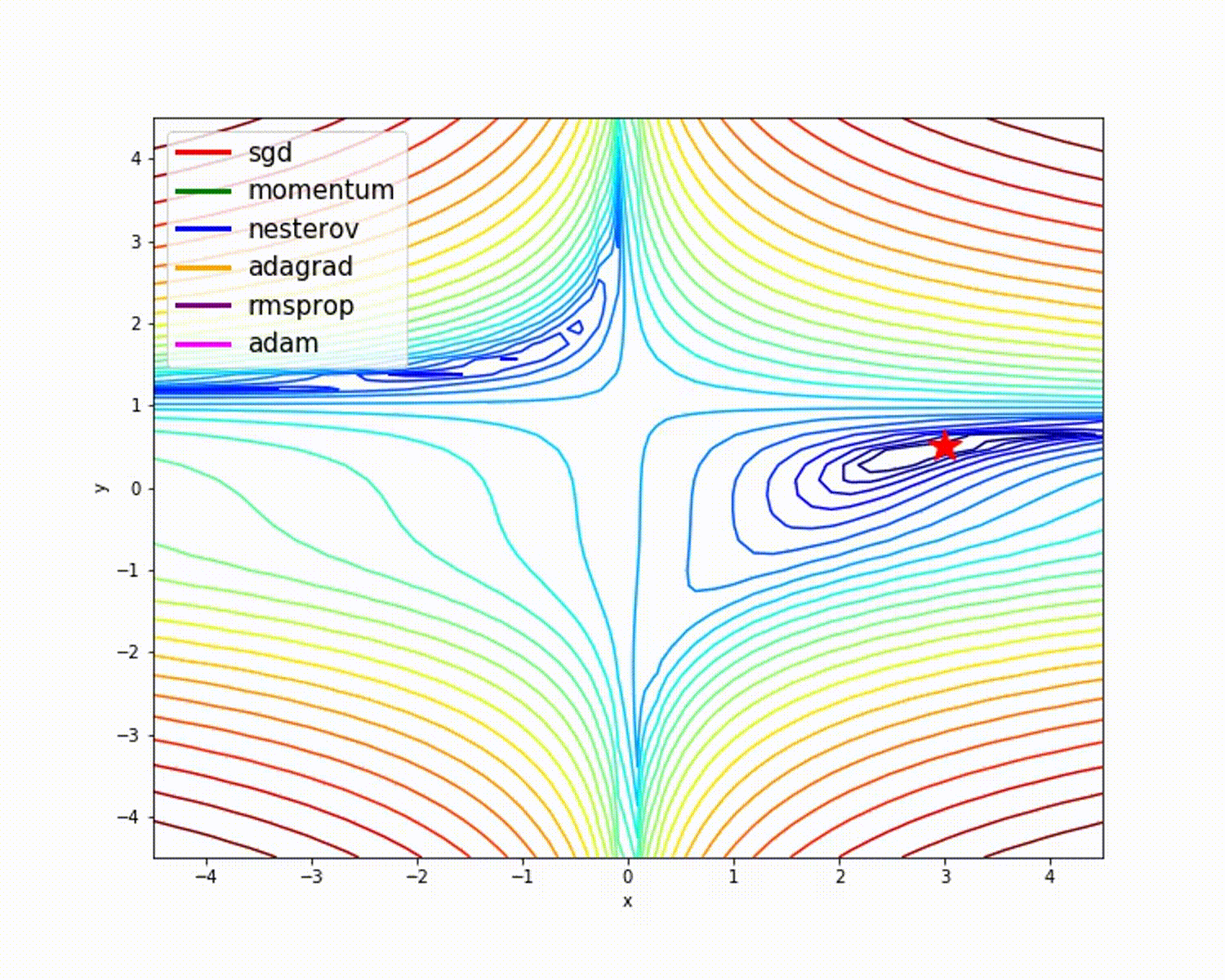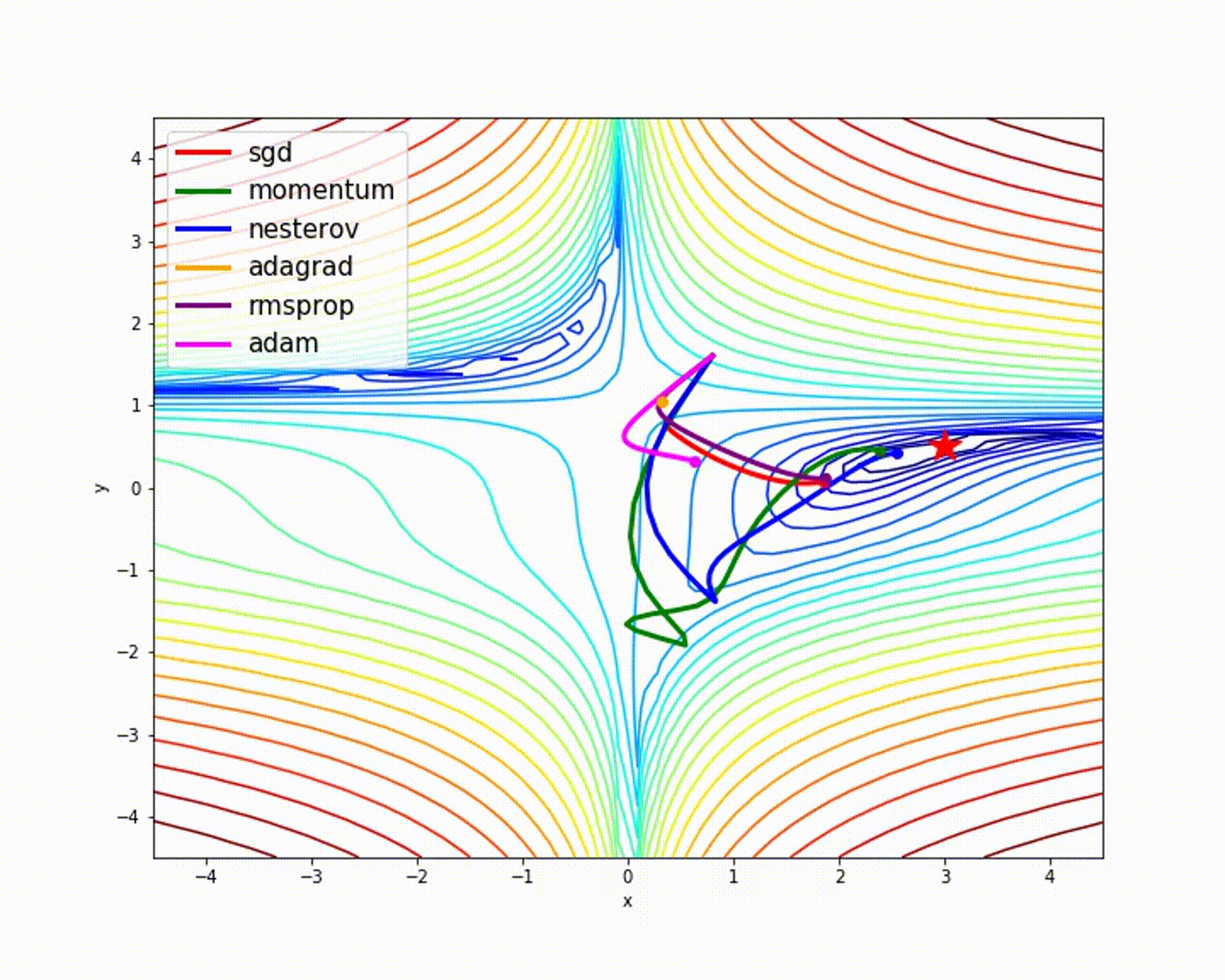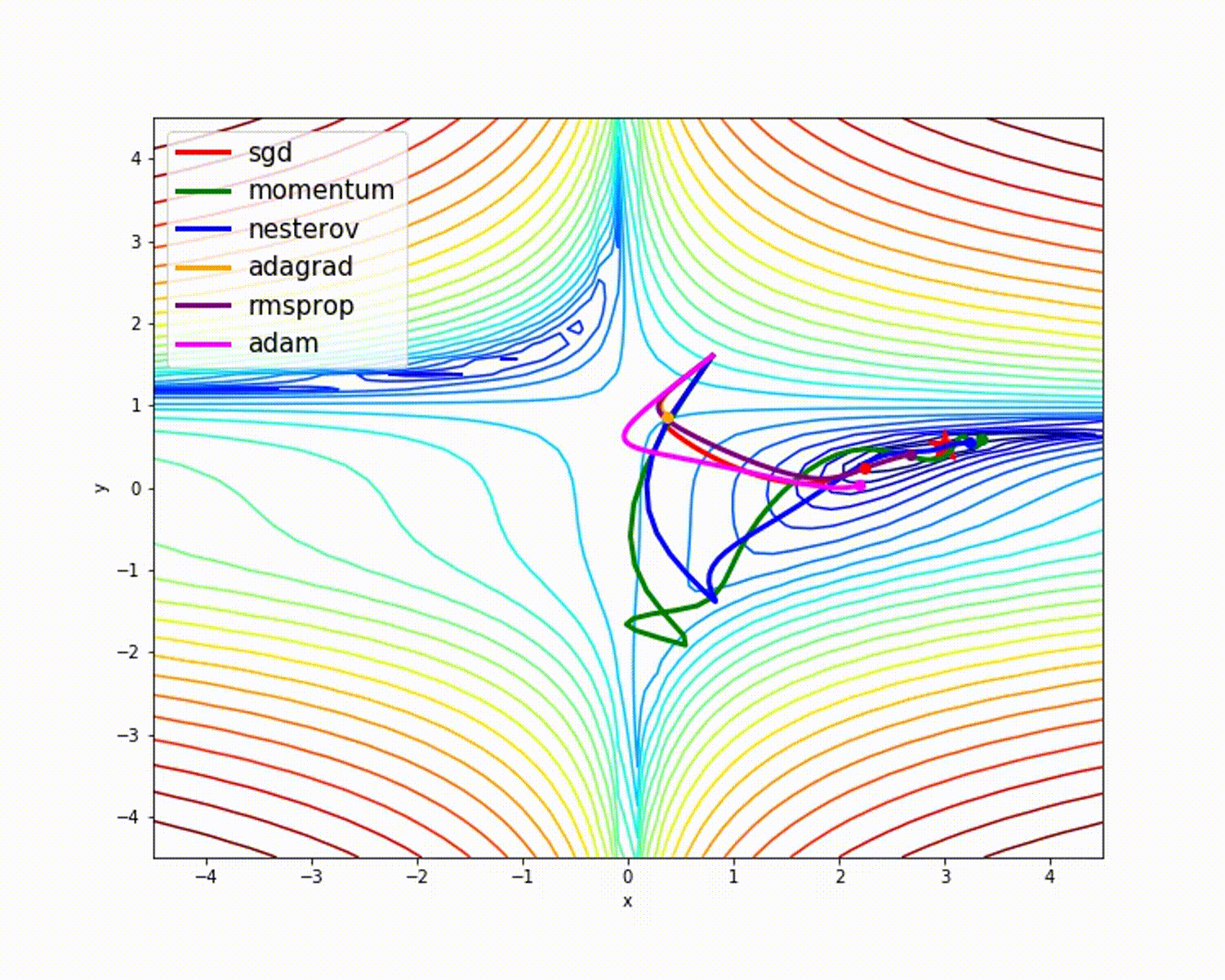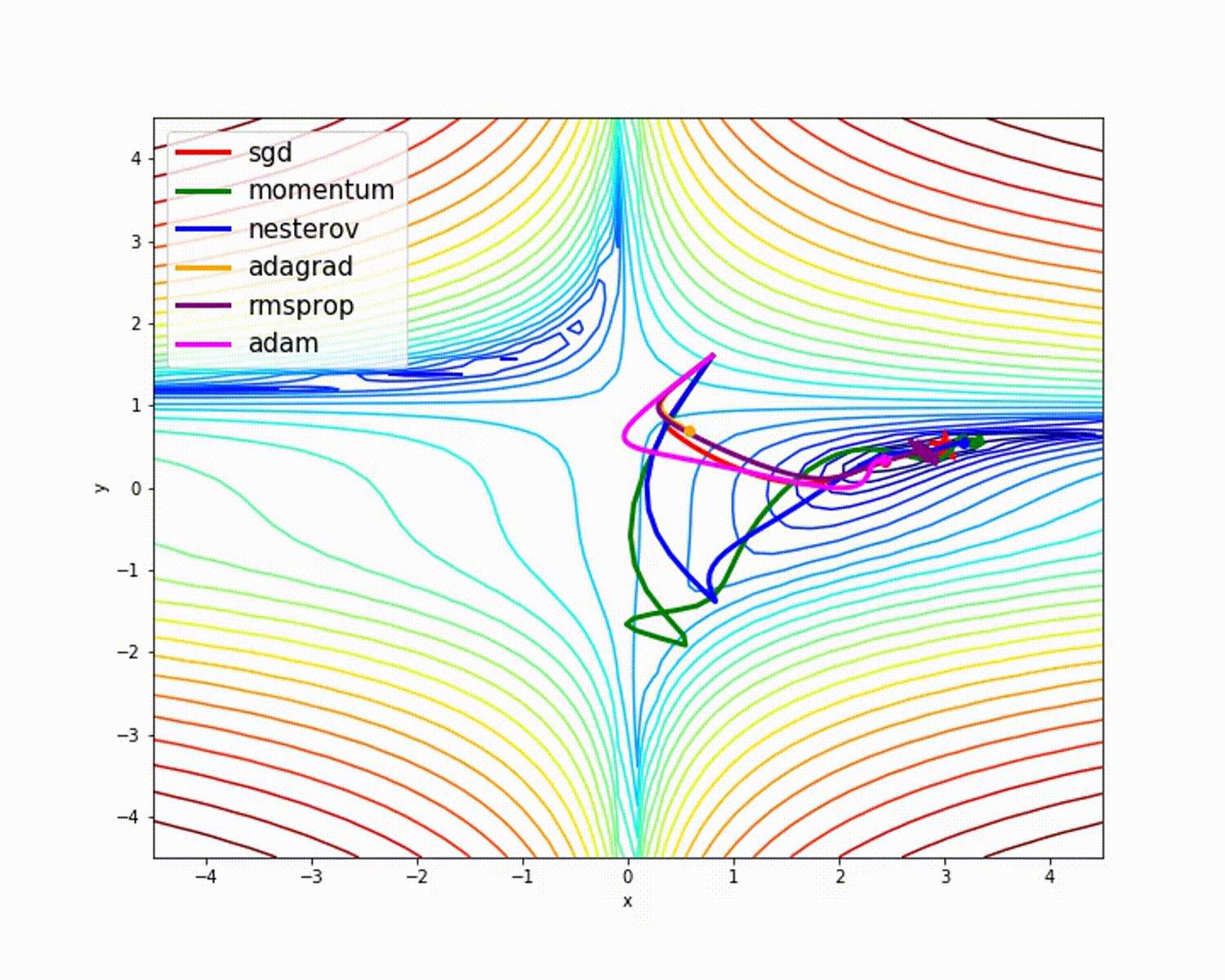
source
As we have seen, the Adam optimizer gives good accuracy compared to other optimizers. The picture above shows how the model learns through iterations. Momentum gives the SGD speed and RMSProp gives the exponential average of the weights for the updated parameters. We have used less data in the above model, but we will see more benefit from optimizers when working with large datasets and many iterations. We've discussed the basic idea of optimizers, and I hope this gives you some motivation to learn more about optimizers and use them!
Resources
- Coursera —
- —
The prospects for neural networks and deep machine learning are enormous, and by the most conservative estimates, their impact on the world will be about the same as the impact of electricity on industry in the 19th century. Those specialists who will assess these prospects before anyone else have every chance to become the head of progress. For such people, we have made a promo code HABR , which gives an additional 10% to the training discount indicated on the banner.

- Machine Learning Course
- Course "Mathematics and Machine Learning for Data Science"
- Advanced Course "Machine Learning Pro + Deep Learning"
- Online bootcamp for Data Science
- Training the Data Analyst profession from scratch
- Data Analytics Online Bootcamp
- Teaching the Data Science profession from scratch
- Python for Web Development Course
More courses
- DevOps
- -
- iOS-
- Android-
- Java-
- JavaScript
Recommended articles
- How to Become a Data Scientist Without Online Courses
- 450
- Machine Learning 5 9
- : 2020
- Machine Learning Computer Vision