Jerdella Algorithm: Solving the Problems of Semantic Madness in Bank IT Systems

Semantic problems in IT systems. What happens when many different people start creating

There is an Old Testament legend about how people in the ancient city of Babylon began to build a tower, but the Almighty mixed their tongues, and the tower was not completed. Still, because the tower was built by hundreds of small groups, which together did not understand each other. And without understanding each other, it is impossible to interact. Indeed, it is simply madness to call one and the same thing, implying it the same, in different words. And there is nothing surprising here.

The Old Testament legend can be easily transferred to modern large companies implementing modern IT solutions. An example of such companies, no doubt, can be attributed to modern Russian banks, which have dozens, if not hundreds of business units, which develop their own subculture of communication, built on their own rules and a unique style of business turnover. Naturally, when forming the IT infrastructure, the style of naming business entities that has been established in the team is taken into account. Over the past ten years, a lot of works on this topic have appeared, for example this [1]. Those who have come across information systems analytics in banks know what it means to do the so-called "mapping" of data, especially if the end systems were made by different teams of analysts, developers and customers or vendors. Usually,60% compilation of mapping is an understanding of the essence and semantics of the transmitted data.

The current trend is to use a set of agile methodologies. Everyone is talking about Agile . You can argue to the point of hoarseness whether it is good for business or harm. But one thing will not make anyone reject. In the course of Agile, many different teams, both within the bank and from different vendors, create a variety of IT solutions for business, and often, without interacting with each other, the teams create their own well-established terminology. And at the moment when integration does occur, the same situation described in the Old Testament happens. How does it not resemble the Babylonian bazaar with its thousands of merchants, shops, goods, holy fools, fakirs and fire-eaters? And so, all these people, armed with different ideas and different thoughts, begin to build the Tower.

XSD ( JSON ) , - . , , «» , Confluence, Zoom Webex, « » , — .

, ESB ( ) -, , , «-» , . … , , . , , - , Kafka. , , , . XML , XSD , , , , JSON, - , «» «». , , , JSON . . , . XSD , . JSON . .

? , - . , ?

.

- . , . MS Excel, , , «» . ( JSON path), — . «». . , :

« »

« »

«20- »

«12- »

« , »

, , , , -. , : , . – “ ”. , , , , , , .

, , , PIP! xslx , . , , Python, .

, – Python. , Python. , , - . , , . – , , . : « , ». — - PyQt Tkinter. , . .

, JSONpath , . , , , Python. , .

. JSON.

. “” 33- . 33 ? – “33” . «». . , , , [2]. . «» . : , , 33- . . . , ABC :

$\$\$\; display\; \$\$\; ABC\; =\; (x\_A,\; x\_B,\; .....,\; x\_Y),\; (1)\; \$\$\; display\; \$\$$

where each x-coordinate at the corresponding position is the number of the corresponding letter of the field comment in the excel file. For example, we have the comment “Individual account number”. Let us compare for it a vector emerging from the origin of coordinates of the Cartesian system in an alphabetical 33-dimensional space, it will look like this: coordinate X _A - corresponds to the number of letters "a". And it is equal to two. X _B - in this case it will be equal to zero, since there is no letter “b” in this statement. The same applies to x _B - there is no letter "c". But x _And - will be equal to 3, since the letter "and" in the comment occurs three times.







Figure 1 . , « » . «»= 2, «» =3. – x_A=2, x=3.

, , ( ) , 33- $$$\vec{S_1}$ « », :

$$

$$\vec{S_1}=(2;0;0;1;0;3;0;0;1;3;0;1;1;1;1;3;0;1;2;1;0;1;0;1;2;0;0;0;0;0;0;0;0)$$

, , « «»» ( , , «» «») « ». $$$\vec{S_2}$ $$$\vec{S_3}$ :

$$

$$\vec{S_2}=2;0;0;0;0;2;0;0;1;2;0;1;0;1;1;1;0;1;1;1;0;1;0;0;1;0;0;0;0;0;0;0;0),$$

$$

$$\vec{S_3}=2;0;0;0;0;3;0;0;0;1;0;1;1;1;2;1;0;1;1;2;0;0;0;0;1;0;0;0;0;0;0;0;0)$$

Now we will find the difference between the vectors in the Cartesian coordinate system of the alphabet space, it is found, respectively, according to the formula well-known from analytical geometry:

$$

$$\vec{∆S_{1,2}}=(x_{,1}-x_{,2};x_{,1}-x_{,2};.....;x_{,1}-x_{,2}) , (2)$$

Where $$$x_{n,1}$ and $$$x_{n,2}$the corresponding vector coordinates for the axis corresponding to the letter.



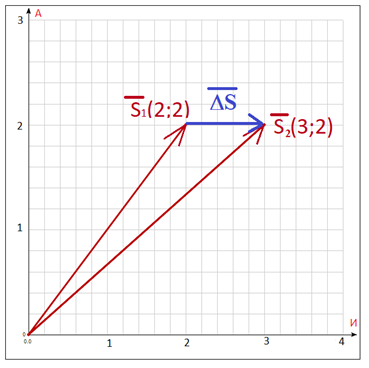
Figure 2. Blue color shows the difference between vectors$$$∆\vec{S}_{1,2}$on the plane of letters - of alphabetical space.



Thus, the vector corresponding to the difference between the statements "Account number of an individual" and "Account number of a physicist" will look like this:

$$$∆\vec{S_{1,2}}=(0;0;0;1;0;1;0;0;0;1;0;0;1;0;0;2;0;0;1;0;0;0;0;1;1;0;0;0;0;0;0;0;0)$, the

vector corresponding to the difference between the statements "Individual account number" and "Client account number" will look like this:

$$

$$∆\bar{S_{1,3}}=(0;0;0;1;0;0;0;0;1;2;0;0;0;0;-1;2;0;0;1;-1;0;1;0;1;1;0;0;0;0;0;0;0;0)$$

,

Further, the length of the calculated difference vectors obtained by the formula:

$$

$$|∆\bar{S_{1,2}}|=\sqrt{({x_1}^2+{x_2}^2+...+{x_33}^2)},(3)$$

If you make an arithmetic calculation, you get:

$$

$$∆S_{1,2}=3.32$$

$$

$$∆S_{1,3}=4.00$$

This mathematically assumes that the phrase “Account number of an individual” is closer in meaning to “Account number of a physicist” than to “Account number of a legal entity”. This is indicated by the lengths of the difference vectors. The shorter the length, the closer in meaning the statements are to each other. If we, for example, take and compare the statements “Account number of an individual” and “number of the branch in which an account of an individual is opened”, we get the figure 6.63. Which will indicate that if the first two statements are close in meaning to the original (the difference in vectors 3.32 and 4.00, respectively), then the third, obviously, will even have a different business essence, despite the seemingly identical set of words ...

You can go further and try, through vectorization, to quantify the closeness of comments in meaning. For this, I propose to use the projection of vectors onto each other. Then find the ratio between the long projection of the compared wind to the length of the one with which it is compared. This ratio will always be less than or equal to one. And accordingly, if the statements are identical to each other, then the projection will merge with the vector onto which the projection is made. The further the compared statement is in meaning, the less the projection will be. If you multiply it by 100%, you can get the degree of correspondence of the vectorized statements in percent. Thus, the projection of the vector$$$\vec{{S_2}^\prime}$ compared statement $$$\vec{S_2}$ on the vector of the original statement $$$\vec{S_1}$ will be found by the following formula:

$$

$$\vec{S_2^\prime}=\frac{(\vec{S_1},\vec{S_2})}{\left|\vec{S_1}\right|}=\frac{x_{1}x_{1}+x_{1}x_{2}+...+x_{1}x_{2}}{{x_{1}}^2+{x_{1}}^2+....+{x_{1}^2}}, (5)$$

Thus, the degree of compliance $$$\delta$ will be calculated using the following formula:

$$

$$\delta=\frac{\left|\bar{S_2^\prime}\right|}{\left|\bar{S_1}\right|}*100$$ = \frac{x_{11}x_{21}+x_{21}x_{22}+...+x_{n1}x_{n2}}{{x_{1}}^2+{x_{1}}^2+....+{x_{1}^2}}*100 , (6)$$

Figure 3. Illustration of a projection$$$S_2^\prime$ vector $$$\vec{S_2}$ per vector $$$\vec{S_1}$...

It is this parameter that is proposed to be taken as a basis for determining the semantic correspondence.

Implementation of the algorithm in Python . A little about apricot. How to set and handle vectors

I named the algorithm Jerdella . Nothing strange, I'm just from Rostov-on-Don.

. , --, , , . , , -, -, -, “”. , .

, , Python , . , . , NumPy. , , NumPy? , – , , - « », . , NumPy. — . , , PIP... Therefore, our Jerdella will use the standard packages included in the PyCharm Community Edition for the Python 3 interpreter .

So, the good thing about Python is that it has the ability to implement a wide variety of data structures. And why are we not satisfied with a list for recording a vector? A list of elements of type int is what you need to define a vector in the alphabetical space and further operations with it.

We have written a number of fundamental procedures, which I will briefly describe below.

How do I set a vector?

I set the vector with the following vector procedure:

def vector(self,a):
    vector=[]
    abc = ["", '', "", "", "", "", "", "", "", "", "", "", "", "", "", "", "", "", "", "",
                "", "", "", "", "", "", "", "", "", "", "", "", ""]
    for char in abc:
        count=a.count(char)
        vector.append(count)
    return(vector)

That is, in the for loop over the elements of the previously prepared list abc , I used the standard operation to find attachments to the count string . After that, using the append method , I filled in a new vector list , which will be the vector for further calculations.

How to calculate the difference in vectors?

To do this, I created a delta procedure that takes two lists as input - a and b .

def delta(self, a, b):
    delta = []
    for char1, char2 in zip(a, b):
        d = char1 - char2
        delta.append(d)
    return (delta)

In the for loop, by iterating over both lists, the difference was counted, added at each iteration step to the end of the delta list , which the procedure ultimately returned as a vector.

How to calculate the length of a vector and thereby estimate the difference?

To do this, I created a procedure len_delta , which takes a list as input, and by iterating over each element of this list (it is also a coordinate in alphabetical space), according to the rule for finding the vector module, calculates the length of the vector.

def len_delta(self, a):
    len = 0
    for d in a:
        len += d * d
    return round(math.sqrt(len), 2)

How to calculate the ratio of the projection onto a vector and thereby estimate the percentage of coincidence?

For this, a simplify procedure was created that takes two lists as input. In it, I implemented formula (6). And here an important point is to determine which vector has the greatest length. For greater clarity in evaluating the coincidence, it is more convenient to project a smaller vector onto a larger one.

def simplify(self, a, b):
    len1 = 0
    len2 = 0
    scalar = 0
    for x in a: len1 += x * x
    for y in b: len2 += y * y
    for x, y in zip(a, b): scalar += x * y
    if len1 > len2:
        return (scalar / len1) * 100
    else:
        return (scalar / len2) * 100

Discussion of the results obtained. Conquering semantic space by structuring it

, , Jerdella . : 1) , , . 2) -. , CRM Siebel ESB, -. , , , -. , , . … . , , , …

… 2 , Agile, , point-to-point, , .

. , , . 2-3 , , . , , , : « » « », « », « », « », , . , 3000 , 500 ? – ? . , - 3000 ?

. «» , . . Python . «». “” , . « ». , , , – .

, :

{'Account number of an individual': [{4.69: 'Client's bank account'}, {6.0: 'Last name'}, {4.8: 'Metal account number'}, {4.8: 'Client number'}]}.

This diagram can also be visualized in graph form. You can do a lot with dictionaries in Python ... To visualize and demonstrate the results, we used the open Internet project www.graphonline.ru . This platform allows you to quickly build a graph written using GraphML .



Figure 4. Graph of the relationship of the entity "Number of an individual". An illustration of the presence of "orbits of semantic correspondence" in an entity.

«» , (3) , , «» , . « » « ». , . , , , . .

? , « » «-». ( $$$\vec{S_1}$ ( 3) $$$\delta$ (5)), . , « » . , « ».

, , , . . .



5. , .

, . … , , . , – ? ? ? — . 80%, , . , . , … - – . , .

, , , , . , , «» ( 6), . «», «», «», - -. , 30% . . , . , , , .





6. «» . , .

. .

«-» . , , - . ? , -.

. - . , . : « - ». , , . « » . , , , . – « ! - »…

, , - , , « », « » « », « », « ». , « ». , . ? ? « »?

, , , , , . – .

, :

[1] . . : . . 2010.

[2]. , . , . . Python. . – . , 2019, — 368 .



P.S. Accenture — ,