Two computer scientists found an idea in a very unexpected place that was just useful to them for a breakthrough in graph theory

In October 2019, Jacob Holm and Eva Rothenberg were leafing through a work they had published a few months earlier - and suddenly realized that they had stumbled upon something serious.
For decades, computer scientists have tried to devise a quick algorithm to determine if edges can be added to a particular graph so that it remains “planar” —that is, so that its edges do not intersect. However, no one has succeeded in improving the algorithm published over 20 years ago.
Holm and Rothenberg were surprised to find that in their workthere is an idea that allowed to improve this algorithm quite strongly. She "sorted out one of the major obstacles to a real algorithm," said Holm, a computer scientist at the University of Copenhagen. "We may have fully covered this issue."
The couple hurried to get down to work on a new article . They presented it in June at the Association for Computing Machinery Symposium on Computational Theory , where they detailed a method for checking a graph for planarity, exponentially superior to the previous version.
“The new algorithm is truly masterful,” said Giuseppe Italiano , a computer scientist at the University of Louis, co-author of a 1996 paper that now describes the second fastest algorithm. "When I was involved in the writing of that work, I did not think that this could happen."
Graphs are collections of vertices connected by edges. They can be used to label everything from social media to road networks and electrical conductors on a board. If in the latter case the graph is not planar, then the two conductors will cross each other, which will lead to a short circuit.
Back in 1913, planar graphs appeared in a complex "communal" puzzle about three houses , published in The Strand Magazine. The publication asked readers to lay communications for three houses, connecting each of them with three energy carriers - water, gas and electricity - so that the communications do not intersect with each other. It doesn't take long to realize that this task is insurmountable.
However, in cases with more complex graphs, it is not always obvious whether they are planar. It's even more difficult to tell if a complex graph will remain planar when you start adding edges to it - as is the case when planning new roads.
Computer scientists have long been looking for an algorithm that can quickly determine if the desired change can be made so that the graph remains planar, without going through each of the parts of the graph when only a small part of it is changed. The 1996 algorithm required a number of steps for this, roughly proportional to the square root of the number of vertices in the graph.
“It's much better than checking everything from scratch every time, but not perfect,” Holm said.
The new algorithm checks for planarity in a number of steps proportional to the cube of the logarithm of the number of vertices in the graph - the improvement is exponential. Holm and Rothenberg of the Danish Technical University achieved this speed-up by taking advantage of a special property of planar graphs they discovered last year.
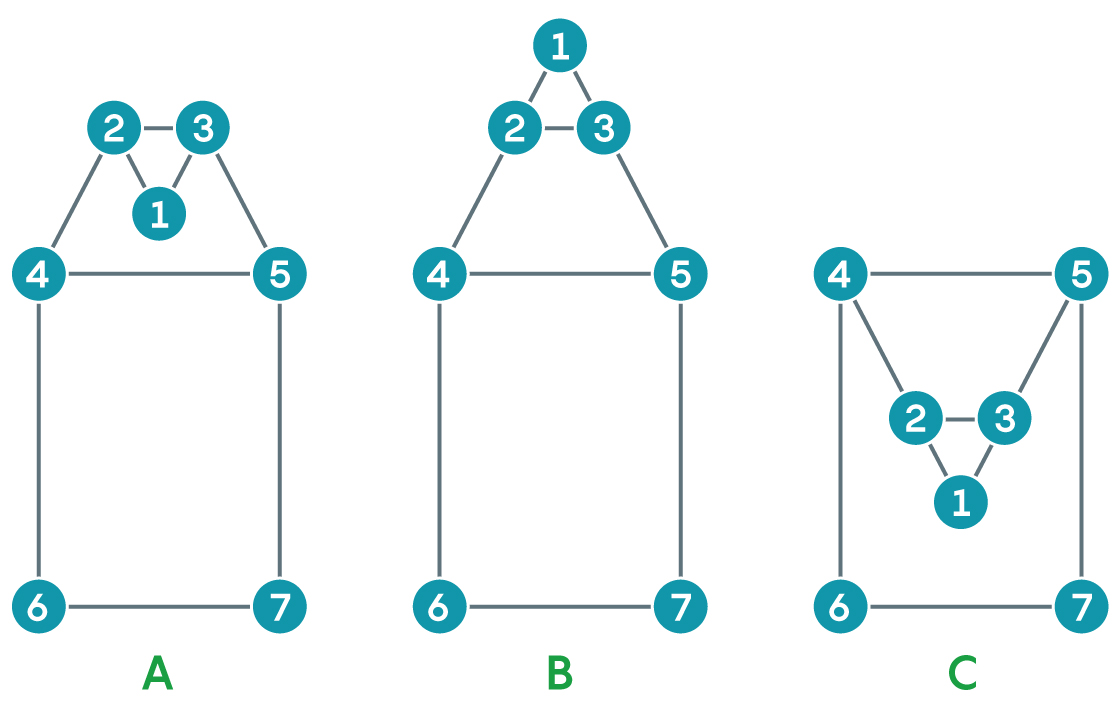
To understand their method, you must first note that the same planar graph can be drawn in different ways . All connections of these options remain the same, however, the edges can be located relative to each other in different ways.
For example, figure A can be changed to figure B by inverting the triangle that makes up vertices 1,2 and 3 relative to the edge connecting vertices 2 and 3. The top of figure B can also be flipped relative to vertices 4 and 5, getting figure C. The figures look like differently, but denote the same graph.
Now imagine that you want to insert a new edge connecting two vertices of a planar graph — say, vertices 1 and 6. To do this, you run a sequence of flips. From the starting position on the left, in two flips, you can transfer vertex 1 to the place where it can be connected to vertex 6 without crossing other edges.

In a 2019 paper, Holm and Rothenberg found that some drawings have more advantages for edge insertion than others. These “good” patterns only need a few flips to add a new edge without breaking planarity.
What they belatedly realized in October is that a flip that brings you closer to a position where you can add a new edge also brings the graph closer to one of the good patterns they've already defined. By showing that a sequence of flips inevitably brings the graph closer to the preferred patterns, a new algorithm can be made to limit the number of flips you may need to find a way to add an edge (if at all possible).
“We realized very quickly that with this new analysis the problem could be solved
an algorithm that is extremely simple in concept, ”said Holm.

Jacob Holm and Eva Rothenberg The
new algorithm performs one flip at a time in search of a solution. As a result, one of two things happens: either the algorithm finds a way to insert the required edge, or the next flip cancels the previous one - after which the algorithm concludes that there is no way to add a new edge.
“We call this algorithm lazy greedy,” Rotenberg explained. "It only makes the changes necessary to accommodate the new rib."
Their new method approximates - but does not match - the performance of the best possible algorithm for such tasks. The new algorithm also has to go through too many steps to be used in most real-world applications - usually graphs are simple enough to be brute-force tested.
But for Holm and Rothenberg, the speed of the algorithm is not as important as the ideas that accelerated it. “There are immediate consequences from this understanding,” Rotenberg said.
Italiano believes it will eventually find real uses. “Sooner or later, it will surely affect what is outside of computer science with mathematics,” he said.
Nobody knows when even faster algorithms may appear. This may require a completely new breakthrough, or the secret ingredient may already exist somewhere, waiting in the wings in a pile of old research.