
Today we will analyze the speech of James Wootton from IBM Quantum at the FDG 2020 conference. We will talk about quantum computing - a potentially promising technology, for which, however, there is little use at the present stage of development. And yet one of them was found in procedural generation.
Let's talk in more detail how to implement it on qubits, and also give the program codes.

Let's start with what quantum computers are and how potentially useful they can be. Let's not go deep into technical details. Let's just mention that quantum computers are a completely different model of computing than digital and analog computers. They don't just speed up conventional software with quanta. Instead, they require a completely different approach to implementing programs, as well as different hardware to run them.

Quantum computing will one day be able to perform certain tasks much more efficiently than digital or analog computing. This will allow us to deal with problems that are currently impossible to solve. After decades of research, many quantum algorithms have been identified that most effectively demonstrate these advantages in relation to a number of possible applications - including in the field of procedural generation. These include optimization, constraint satisfaction, graph analysis, and others.
Building computers capable of performing quantum computing is a daunting task in and of itself, and has been in the making for years. One of the important parameters for describing a quantum device is the number of qubits. In fact, these are the same bits, but implemented in a quantum way - and therefore having more states than the usual 0 and 1. In the context of quantum physics, we can write the bit values using a pair of orthogonal vectors: | 0⟩ and | 1⟩. In the case of qubits, the description of the states will be supplemented with complex amplitudes c 0 and c 1 , which satisfy the condition: | c 0 | 2 + | c 1 | 2= 1, due to which a larger number of states of the qubit c 0 | 0⟩ + c 1 | 1⟩ is achieved.

We need many thousands of qubits to run flagship algorithms, which we won't have in the next few years.
Currently, we do not have many thousands of qubits or even one thousand at our disposal. To be honest, we don't even have a hundred qubits. The largest device currently available to us has 65 qubits. While this is not enough to run the most interesting and efficient algorithms we know of, even this number of qubits can provide results that are not expected from conventional computers. This is evidenced by the complexity of emulating such devices, for which you will need to rent the world's largest supercomputer.
So quantum hardware may offer us unique answers, but over the decades we have not learned how to ask the right questions. Therefore, the main goal of our current research is to try to figure out as soon as possible how to do something useful with these machines.

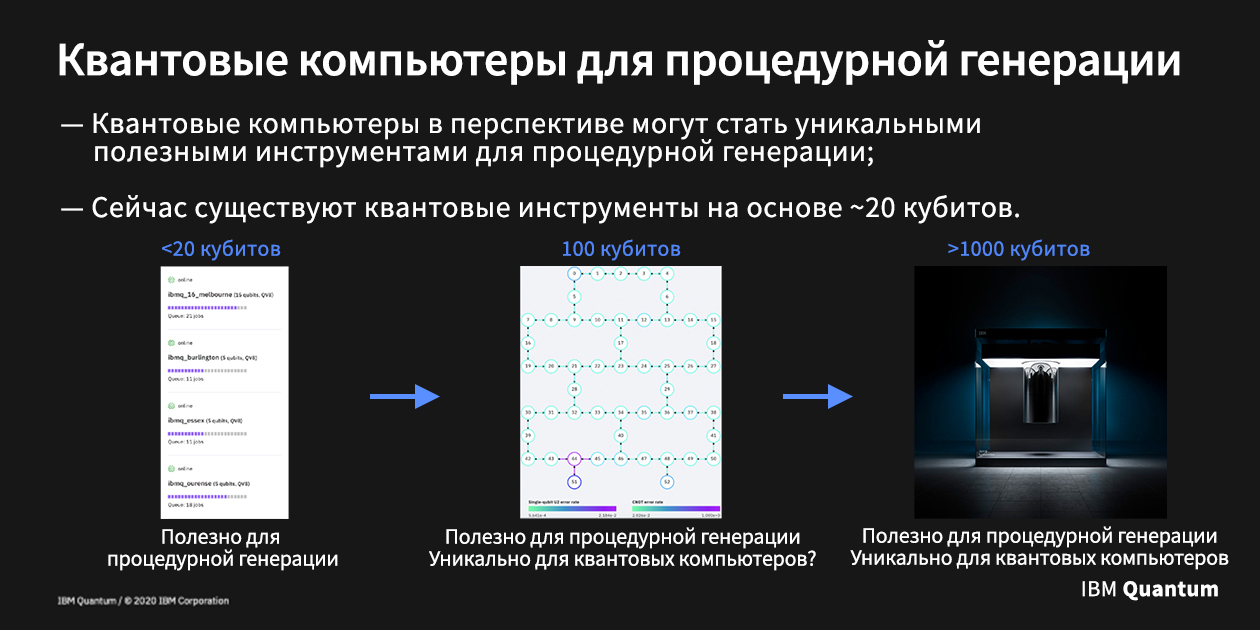
There are also devices of more modest power, consisting of about 20 qubits. And quantum programs using up to 15 qubits were even made available by IBM for free. In addition, they have created emulation software to aid in the design and testing of quantum programs. And while emulating more than 50 qubits is a daunting computational task, even your laptop can handle emulating roughly 20 qubits without any problems.
All factors together make 20 qubits a milestone. Regardless of whether we are using real quantum hardware or its emulation, running quantum software of this level is not too difficult.

So what does this all mean for procedural generation? Depends on which of the three eras you are targeting: today's one, ready to provide only dozens of qubits; for the near future, when devices will have hundreds of qubits; or to the distant future, when more than a thousand qubits will be available to us.
If we talk about today, quantum software, focused on the power of only 20 qubits, still cannot do anything unique. The very fact that we can run it on an emulator means you don't even need quantum hardware. But can quantum programs still do anything useful? Can we write a 20-qubit quantum program that produces results that are useful to the real end user?
If we can achieve really useful results with 20 qubits, this effect will only multiply over time and more computing power. The middle era will be the era of research into more and more sophisticated methods of quantum computing, including effective for procedural generation. We'll move on to creating tools that we probably wouldn't have thought of if we hadn't thought in terms of quanta.
But let's not get ahead of ourselves. The first step towards the era of expanding utility is to prove that even 20-qubit quantum software can be useful. This is what we will do.
Now it's time to clarify some details.
Procedural generation means we need to generate something. But what?
Terrain generation is the most obvious, so let's start with that.
Perlin noise is a ubiquitous tool for procedural terrain generation. But there is another, much less complicated method of creating it - using a set of random points with their subsequent blurring. The implementation of something like this seemed to us a more achievable goal for the first step, so we will take it as a basis.
Let's start by developing a way to encode heightmaps in the form of quantum circuits, which are fundamental elements of quantum software. They bear some resemblance to the Boolean circuit models for digital computing. Qubits are essentially the same bits that undergo different changes as calculations are performed.

We will work with black and white images, where the brightness of a pixel can have a value from 0 to 1. In the same way, they can be mistaken for height maps. Once we learn how to encode these heightmaps as schematics, we can manage them. The encoding used aims to compress as many points as possible into as few qubits as possible. This method does not leave much flexibility to provide convenient and flexible control. At the same time, almost any change in the circuit will cause interference effects.
We mainly use operations that can be viewed as partial forms of the NOT gate. Does NOT change the value from 0 to 1 and vice versa for normal bits. With quantum gates, we can parameterize this element to perform an operation that can do half of NOT, or a quarter, or any other fractional part that can be represented by a set of 2 n amplitudes of n qubits.
The function below converts the original image to a quantum circuit:
def height2circuit(height):
#
L = max(max(height))+1
#
grid = make_grid(L)
#
n = 2*int(np.ceil(np.log(L)/np.log(2)))
#
state = [0]*(2**n)
#
H = 0
for bit string in grid:
(x,y) = grid[bit string]
if (x,y) in height:
h = height[x,y]
state[ int(bit string,2) ] = np.sqrt( h )
H += h
#
for j,amp in enumerate(state):
state[ j ] = amp/np.sqrt(H)
#
qc = QuantumCircuit(n,n)
qc.initialize(state,range(n))
# Qiskit
# qc.initialize( state, qc.qregs[0])
return qcThen we need to do the opposite process - transform the quantum circuit into an image:
def circuit2height(qc):
#
n = qc.num_qubits
grid = make_grid(int(2**(n/2)))
#
ket = qi.Statevector(qc.data[0][0].params)
qc.data.pop(0)
#
ket = ket.evolve(qc)
#
p = ket.probabilities_dict()
#
max_h = max( p.values() )
#
height = {}
for bit string in p:
if bit string in grid:
height[grid[bit string]] = p[bit string]/max_h
return heightIf we apply this operation to all the qubits, we can see how the heightmap changes as the fraction increases. You will get something like a blur effect. Interference effects will then occur, creating a pattern that cannot be achieved with simple blur.
In the example above in (a), we start with a pair of seemingly arbitrary points. Gradually, they undergo blurring, after which interference effects are superimposed on them. This leads to the appearance of a pattern - in our case, like a checkerboard on (f). This particular result has a clear connection to the two pixels we started with. If you take other data as a starting point, the result will also be completely different.
Quantum Blur has been developed and tested on several game jams. It is mainly used to generate textures and level maps.

After generating these maps, we use them for the quantum analogue of Perlin's high frequency noise.
So now we create the main profile - for example, islands - in some other way - as in © in our example. Then we need an initial set of pixels as in (a). We quantum blur it to generate a pattern like (b). After that we apply it to the main profile to create the final landscape.
You can see a 2D example here, as well as the 3D rendering that was used in the IBM QiskitBlocks tutorial game. Details such as information about the type of grass and the placement of trees in 3D rendering have also been developed using quantum operations.

Since RGB images are typically three elevation maps aligned together, we can manipulate these images as well. This way it is easy to create some weird pictures using overlay. More difficult, but more effective - encoding a pair of images and creating a teleportation effect between them.
Quantum teleportation transfers information between qubits. So we take two qubit registers of the same size and just change their states. Let's use this operation to create a transition animation.

A similar coding idea can also be used for other forms of data. Wootton tried to use it in music:
and the level of Mario:
Here are two more examples that are important to us. One of them is a game studio using this method for procedural generation in a future game. The project has a sci-fi setting, and the quantum method brings a genuine flavor of science to it.
Also, the artist Libby Heaney used some of these ideas as a starting point for her work.
The quantum nature of computation is emphasized in both of these cases: it is important for the user that the results come from the quantum domain of the algorithm space, and not just brilliant linear algebra.
The method described here is more suitable for emulation than for real quantum hardware, but this will soon change. In fact, one of the largest quantum devices at IBM has also been used for procedural generation, albeit in a completely different way.
In the meantime, you can try out the quantum blur effect yourself. It is written in Python , but there is a plugin for Unity as well . Perhaps they will be useful to you.
Link to the full article: here .